Balbharti Maharashtra State Board Class 11 Political Science Important Questions Chapter 10 The World Since 1945 – II Important Questions and Answers.
Maharashtra State Board 11th Political Science Important Questions Chapter 10 The World Since 1945 – II
1A. Choose the correct alternative and complete the following statements.
Question 1.
The first NAM summit was held at ____________ (Bangkok, Camp David, Bandung, Belgrade)
Answer:
Belgrade
Question 2.
During the Cold War, western capitalist economies, aligned to the USA were called as ____________ countries. (First World, Second World, Third World, Non-Aligned)
Answer:
First World
Question 3.
The beginning of detente was 1972, summit meeting at ____________ (New York, Camp David, Moscow, China)
Answer:
Moscow
Question 4.
In 1978, the conference at Camp David was to reduce tensions between ____________ (USA – USSR, USA – China, Arab World – Israel, India – Pakistan)
Answer:
Arab World – Israel
![]()
Question 5.
The SAARC was established in ____________ (1967, 1985, 1992, 1989)
Answer:
1985
Question 6.
Iran withdrew from the ____________ military alliance in 1979. (CENTO, SEATO, NATO, NAM)
Answer:
CENTO
Question 7.
In 1991, Commonwealth of Independent States was created after the disintegration of the ____________ (USA, USSR, Germany, CENTO)
Answer:
USSR
Question 8.
____________ tried to reform the system in the USSR. (Khruschev, Breznev, Yeltsin, Gorbachev)
Answer:
Gorbachev
1B. Identify the incorrect pair in every set, correct it and rewrite.
Question 1.
(a) Soviet Union – Brezhnev
(b) Egypt – Nasser
(c) Czechoslovakia – Tito
Answer:
(c) Yugoslavia – Tito
Question 2.
(a) SAARC – Maldives
(b) BRICS – Brazil
(c) NAM – USA
Answer:
(c) Capitalist bloc – USA
![]()
1C. State the appropriate concept for the given statement.
Question 1.
Reduction of tensions and conflicts.
Answer:
Detente
Question 2.
Principle of active participation in world affairs peacefully and without joining any military alliances.
Answer:
Non-alignment
Question 3.
The collective name for developing countries.
Answer:
Third World countries
Question 4.
Agreement signed in 1978 at Camp David.
Answer:
‘Framework for Peace for Middle East
Question 5.
Special agreements regarding economic relationships are made by a group of nations.
Answer:
Trade Bloc
Question 6.
The term used to indicate “openness” i.e., freedom of expression.
Answer:
Glasnost
1D. Answer in one sentence.
Question 1.
Which was the first direct confrontation between the USA and USSR during the Cold War?
Answer:
The first direct confrontation between the USA and USSR during the Cold War was the Cuban Missile Crisis.
![]()
Question 2.
Which nations were referred to as Second World during the Cold War?
Answer:
Eastern Socialist economies aligned with the Soviet Union were referred to as ‘Second World’ during the Cold War.
Question 3.
When and where was the first NAM summit held?
Answer:
The first NAM summit was held in 1961 at Belgrade (Yugoslavia).
Question 4.
Which was the joint (US – USSR) Space flight in 1975?
Answer:
The Apollo- Soyuz space flight, was the joint (US – USSR) space fight in 1975.
Question 5.
Who signed the agreement at Camp David in 1978?
Answer:
Egyptian President Anwar el Sadat and Israeli Prime Minister Menachem Begin in the presence of US President Jimmy Carter signed the agreement at Camp David in 1978.
Question 6.
What are the common types of trade barriers?
Answer:
Tariffs and quotas are the common types of trade barriers.
Question 7.
Where is the SAARC Secretariat?
Answer:
The SAARC Secretariat is at Kathmandu (Nepal).
Question 8.
What do trade agreements generally focus on?
Answer:
Trade agreements generally focus on relaxation or even the elimination of trade barriers.
![]()
Question 9.
Who initiated the Islamic Revolution in Iran (1979)?
Answer:
Ayatollah Khomeini initiated the Islamic Revolution in Iran(1979).
Question 10.
What is described as New Cold War?
Answer:
The detente between the USA and USSR gradually ended in 1979 and this period is described as New Cold War.
Question 11.
Name the two policies advocated by Gorbachev.
Answer:
Glasnost and Perestroika are the two policies advocated by Gorbachev.
Question 12.
Name the countries where East European revolutions took place in 1989-1990?
Answer:
Poland, Bulgaria, Romania, Czechoslovakia, Hungary had revolutions in the period 1989-1990.
Question 13.
What caused the Cold War to come to an end?
Answer:
The disintegration of the USSR in 1991 caused the Cold War to come to an end.
Question 14.
Name the countries created due to the splitting up of Yugoslavia.
Answer:
Bosnia, Croatia, Herzegovina, Montenegro, Serbia were created due to the splitting up of Yugoslavia.
Question 15.
Name the two countries formed due to the splitting of Czechoslovakia.
Answer:
Slovakia and the Czech Republic were the two countries formed due to the splitting up of Czechoslovakia.
![]()
1E. Complete the sentences by selecting the appropriate reason.
Question 1.
The non-Aligned Movement was established in 1961 because
(a) some countries like India, Egypt, etc. wanted to form their own power bloc.
(b) it was a regional organization of newly independent nations.
(c) it consisted of countries that did not want to align to any power bloc or join any military alliance.
Answer:
(c) it consisted of countries that did not want to align to any power bloc or join any military alliance.
Question 2.
The Cuban Missile Crisis laid the foundations of detente as it
(a) led to an escalation of cold war tensions.
(b) led to an immediate pileup of nuclear missiles.
(c) brought in a realization of possible nuclear confrontation and the need to reduce tensions.
Answer:
(c) brought in a realization of possible nuclear confrontation and the need to reduce tensions.
1F. Find the odd word in the given set.
Question 1.
Nkrumah, Sukarno, Nasser, Nixon.
Answer:
Nixon (not a NAM leader)
Question 2.
Vietnam, Korea, Sri Lanka, Cuba.
Answer:
Sri Lanka (not affected by Cold War)
Question 3.
Mao Zedong, Khrushchev, Gorbachev, Brezhnev.
Answer:
Mao Zedong (Chinese leader)
![]()
Question 4.
ASEAN, NAFTA, SAARC, EU.
Answer:
NAFTA (trade agreement not an organization)
1G. Expand the abbreviations.
Question 1.
- SAARC
- ASEAN
- OPEC
- NIEO
- NAFTA
- OAS
- WTO
Answer:
- SAARC – South Asian Association for Regional Cooperation.
- ASEAN – Association of South-East Asian Nations
- OPEC – Organisation of the Petroleum Exporting Countries
- NIEO – New International Economic Order
- NAFTA – North American Free Trade Agreement.
- OAS – Organisation of American States.
- WTO – World Trade Organisation.
1H. Arrange in a chronological order citing the appropriate dates per event.
Question 1.
- Cuban Missile Crisis
- Arab-Israel War
- Apollo-Soyuz Space Flight
- Founding of SAARC
- Founding of NAM
- Founding of ASEAN
- Soviet Invasion of Afghanistan
- Disintegration of USSR
- Formation of EU
- Formation of WTO
Answer:
- Founding of NAM – 1961
- Cuban Missile Crisis – 1962
- Founding of ASEAN – 1967
- Arab – Israel War – 1973
- Apollo-Soyuz Space Flight – 1975
- Soviet invasion of Afghanistan – 1979
- Founding of SAARC – 1985
- The disintegration of USSR – 1991
- Formation of EU – 1992
- Formation of WTO – 1995
![]()
2A. State whether the following statements are true or false with reasons.
Question 1.
In 1962, the USA established a naval blockade around Cuba.
Answer:
This statement is True.
- In 1962, Nikita Khrushchev of the USSR decided to make Cuba into a Russian base by placing nuclear missiles there.
- This would be a direct threat and so the USA retaliated with a naval blockade of Cuba.
Question 2.
The Non-Aligned Movement had great significance.
Answer:
This statement is True.
- After the Second World War, the two superpowers i.e., the USA and USSR, had begun the Cold War which led to many military alliances being created.
- Many Third World countries, which had recently gained freedom from colonial rule, did not want to ally with any power bloc. So in 1961, the NAM was formally established at Belgrade by heads of India, Yugoslavia, Egypt, Ghana, Indonesia, etc.
Question 3.
Non-Alignment means the country is internationally passive.
Answer:
This statement is False.
- Nonalignment means that a member country should not be a member of any military alliance in the context of the Cold War.
- It does not mean passivity or neutrality in international politics but means that members actively participate in world affairs to promote security, peace, and development.
Question 4.
The Moscow Summit led to an escalation of the Cold War.
Answer:
This statement is False.
- In 1972, President Nixon (USA) and General Secretary of the Communist Party of Soviet Union. Brezhnev met at Moscow.
- The summit signaled the beginning of the era of detente i.e. USA and USSR tried to reduce tensions of the Cold War
![]()
Question 5.
Mikhail Gorbachev as president of the USSR changed the course of world politics.
Answer:
This statement is True.
- Gorbachev introduced the policies of ‘Perestroika’ (reconstruction of the Soviet political and economic system) and ‘Glasnost’ (openness).
- During his tenure, there were popular uprisings against Communist regimes in East European countries like Poland, Bulgaria, Czechoslovakia, etc.
- The USSR ceased to exist and in its place, 15 new countries (CIS) were created (1991).
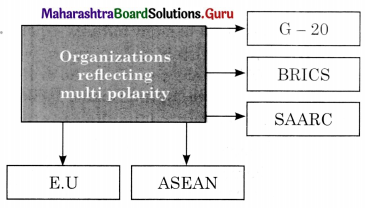
Question 6.
Post-1991 can be called ‘the Era of Multi polarity’.
Answer:
This statement is True.
- After the collapse of the USSR, the USA remained the only superpower due to its military, technological and economic might.
- However, many regional or economic organizations such as OPEC, European Union, G-8, G-20, SAARC, ASEAN, African Union, BRICS, etc. also play a vital role in world politics and international relations.
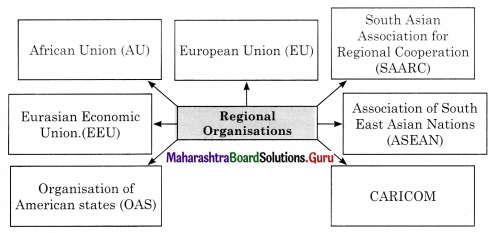
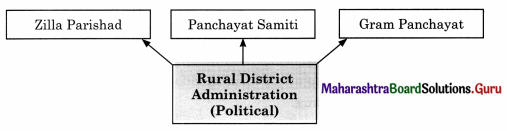
2B. Complete the concept maps.
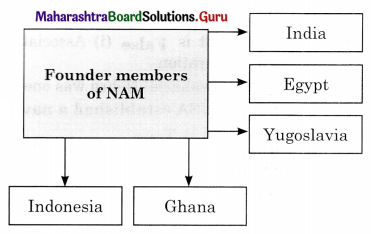
Question 1.
Answer:
![]()
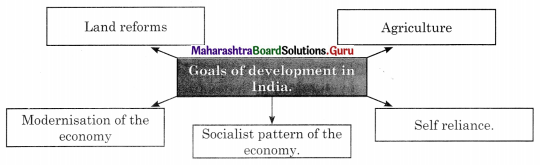
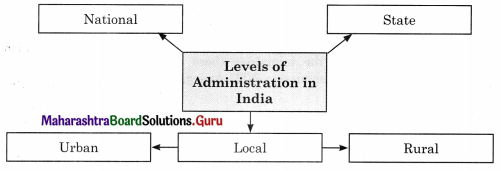
Question 2.
Answer:
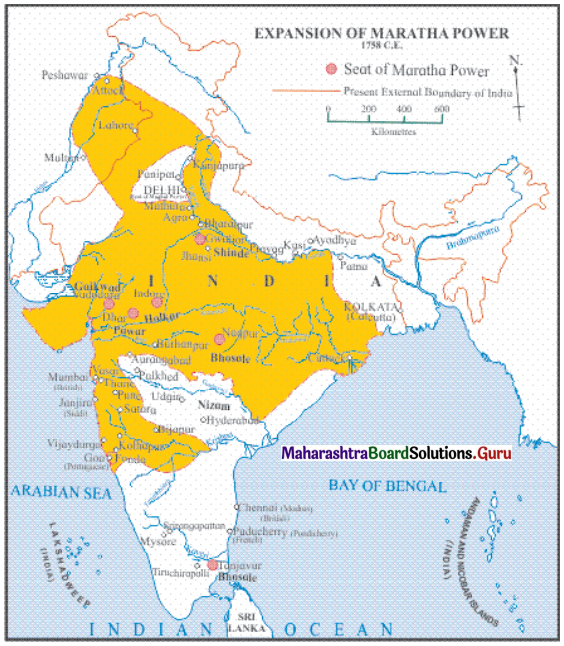
2C. Observe the given map and answer the following questions.
Question 1.
Map of East Europe today.
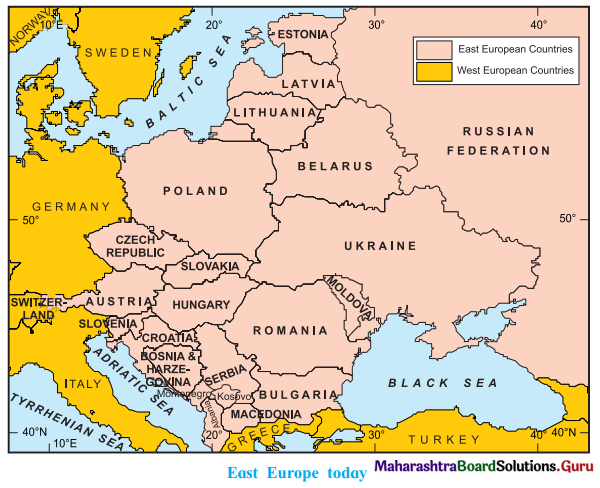
Question i.
Name some countries bordering the Adriatic sea.
Answer:
Italy, Croatia, Albania, Greece, Slovenia.
![]()
Question ii.
Write the neighbouring countries of Poland.
Answer:
Czech Republic, Ukraine, Germany, Belarus.
3. Answer the following.
Question 1.
Write about the US naval blockade in 1962.
Answer:
A naval blockade is prohibiting ships from entering the port of a country. This is done by using the Navy, The United States Navy established a blockade around the island to prevent any offensive weapons from entering Cuba. This was done in retaliation to the USSR using Cuba as a strategic missile base.
Question 2.
Write about the Cuban Missile Crisis.
Answer:
In spite of attempts to create goodwill between the two power blocs (such as at Camp David Summit), tensions continued to escalate. In 1962, the first direct confrontation of the Cold War took place. This was the Cuban Missile Crisis. Cuba is a small nation off the coast of the USA. It had the support of the USSR. Due to its’ strategic location, then Soviet Premier, Khrushchev, decided to convert Cuba into a Soviet base by placing nuclear missiles there. This was a serious, direct threat to the USA which retaliated with a naval blockade of Cuba. There was a real possibility of a nuclear war. But, both superpowers realized the need to prevent such a situation and USSR withdrew its missiles from Cuba.
Question 3.
Explain Non-Alignment.
Answer:
A group of Third World countries (i.e., from Asia, Africa, South America), most of whom had recently gained sovereignty from colonial rule, refused to join any Cold War alliances. This laid the foundation for the Non- Aligned Movement. Which was formally established at the Belgrade Conference (1961) with 25 member nations. Some of the founding members were Marshall Tito (Yugoslavia) Jawaharlal Nehru, (India), Gamal Nasser (Egypt), Nkrumah (Ghana), Sukarno (Indonesia).
The concept of Non-alignment is based on two main principles:
- independent understanding of world affairs
- peace approach.
Thus it does not mean political passivity or neutrality. In fact, the idea was active participation in world affairs to promote peace and development.
The purposes of NAM were
- not to ally with any power bloc
- opposition to any military alliance
- freedom to take independent policy decisions with regard to international affairs.
![]()
Question 4.
What were the consequences of the collapse of the USSR?
Answer:
The consequences of the collapse of the USSR included-
The Commonwealth of Independent States came (CIS) into existence and finally, new countries were formed such as Ukraine, Belarus, Georgia, Armenia, etc.
Other changes due to the disintegration of the Soviet Union included:
- reunification of Germany in 1990.
- splitting Yugoslavia into Serbia, Bosnia, Croatia, Slovenia, etc.
- splitting of Czechoslovakia into the Czech Republic and Slovakia.
The disintegration of the USSR signified the end of the Cold War and the USA emerged as the only superpower (unipolarity).
Question 5.
Write about the policies of Gorbachev.
Answer:
There were significant changes in Soviet policy under Mikhail Gorbachev (President of USSR). He introduced the policies of Glasnost (openness i.e., transparency in governance and freedom of expression) and Perestroika (reconstruction of the political and economic system).
His new foreign policy included:
- withdrawal of Soviet troops from Afghanistan
- stopping of the arms race with the US and focused on arms control
- opening a dialogue with China.
Gorbachev also tried to reform domestic politics. Control of the Communist Party ended and people were given the right to criticize the government. On 25th December 1991, Gorbachev resigned and the next day the USSR as a country ceased to exist. This led to the Commonwealth of Independent States is established.
Question 6.
Write about the objectives of SAARC.
Answer:
South Asian Association for Regional Cooperation (SAARC) was established in 1985.
The objectives of SAARC are
- to promote the welfare of the people of South Asia and to improve their quality of life.
- to accelerate economic growth, social progress, and cultural development in the region.
- to contribute to mutual trust, understanding, and appreciation of one another’s problems.
- to promote active collaboration and mutual assistance in the economic, social, cultural, technical, and scientific fields and to strengthen cooperation with other developing countries.
![]()
Question 7.
Write about CIS (1991)
Answer:
Commonwealth of Independent state (CIS) was created after the disintegration of the Soviet Union in 1991. The members were the former states of the USSR. The founder members were Russia, Ukraine, and Belarus. Subsequent members were Armenia, Azerbaijan, Georgia, Kazakhstan, Kyrgyzstan, Moldova, Tajikistan, Turkmenistan, and Uzbekistan.
Common affairs were conducted on a multilateral, interstate basis. It provided a framework for military, foreign policy, and economic cooperation between members.
Question 8.
Make a list of countries that were created after the disintegration of the Soviet Union.
Answer:
After the disintegration of the Soviet Union (1991) many countries like Russia, Ukraine, Belarus, Armenia, Azerbaijan, Estonia, Georgia, Kazakhstan, Kyrgyzstan, Latvia, Lithuania, Moldova, Tajikistan, Turkmenistan, and Uzbekistan were created.
Question 9.
List the Non-Aligned Summits that have occurred since 1961.
Answer:
| Summit year | Place |
| 1st – 1961 | Belgrade (Yugoslavia) |
| 2nd – 1964 | Cairo |
| 3rd – 1970 | Lusaka (Zambia) |
| 4th – 1973 | Algiers (Algeria) |
| 5th – 1976 | Colombo (Sri Lanka) |
| 6th – 1979 | Havana (Cuba) |
| 7th – 1983 | New Delhi (India) |
| 8th – 1986 | Harare (Zimbabwe) |
| 9th – 1989 | Belgrade (Yugoslavia) |
| 10th – 1992 | Jakarta (Indonesia) |
| 11th – 1995 | Cartagena (Colombia) |
| 12th – 1998 | Durban (S. Africa) |
| 13th – 2003 | Kuala Lampur (Malaysia) |
| 14th – 2006 | Havana (Cuba) |
| 15th – 2009 | Egypt |
| 16th – 2012 | Tehran (Iran) |
| 17th – 2016 | Porlamar (Venezuela) |
| 18th – 2019 | Baku (Azerbaijan) |