Balbharti Maharashtra State Board Class 11 Sociology Important Questions Chapter 3 Basic Concepts in Sociology Important Questions and Answers.
Maharashtra State Board 11th Sociology Important Questions Chapter 3 Basic Concepts in Sociology
Choose the correct alternative and complete the statements.
Question 1.
An ………………… is a group or category to which people feel they do not belong.
(in-group / out-group / voluntary group)
Answer:
out-group
Question 2.
…………………. membership is based on deliberate choice.
(Involuntary group / Small group / Voluntary group)
Answer:
Voluntary group
![]()
Question 3.
In ……………………. group the relations among its members are normally indirect.
(secondary / primary / voluntary)
Answer:
secondary
Question 4.
A group that guides our behaviour and attitudes, is called as …………………
(reference group / voluntary group / primary group)
Answer:
reference group
Question 5.
………………. laws are not written but orally transmitted.
(Enacted / Customary / External)
Answer:
Customary
Question 6.
…………….. are more rigid than folkways.
(Customs / Rules / Mores)
Answer:
Mores
Question 7.
A process of disengagement from a role that is central to one’s self identity is role ………………..
(conflict / exit / performance)
Answer:
Exit
Question 8.
By social ……………….. we mean the position of a person.
(status / role / group)
Answer:
status
Question 9.
Along with the likeness, society is also based on ………………….
(awareness / differences / age)
Answer:
differences
Question 10.
Different types of social relationships are required for the of society.
(reciprocity / likeness / existence)
Answer:
existence
Question 11.
Social behaviour of the people is evaluated by a mechanism of social …………….. in society.
(area / control / nature)
Answer:
control
Question 12.
…………………. known as ‘standards of group behaviour’.
(Norms / Culture / Society)
Answer:
Norms
Question 13.
No society is ……………………
(static / dynamic / normative)
Answer:
static
Question 14.
A definite territory to fulfil common objectives of a group of people is known as ………………..
(Society / Social group / Community)
Answer:
community
![]()
Question 15.
People living in a community establish their ………………..
(social role / interest / social relationships)
Answer:
social relationships
Question 16.
……………. is the physical basis of community.
(Locality / Group / Status)
Answer:
Locality
Question 17.
Social group is a system of …………………..
(social status / social group / social interaction)
Answer:
social interaction
Question 18.
‘We feeling’ leads to …………………. consciousness.
(collective / political / religious)
Answer:
collective
Question 19.
………………….. is the smallest of all social groups.
(Dyad / Primary Group / Triad)
Answer:
Dyad
Question 20.
The term ………………… was coined by Charles Horton Cooley.
(Primary Group / Secondary Group / Triad)
Answer:
Primary Group
Question 21.
………………… is the first sociologist to emphasise the importance of interaction processes within groups.
(Charles Elwood / George Simmel / Charles Horton)
Answer:
George Simmel
Correct the incorrect pair.
Question 1.
(a) Political parties, trade unions – Voluntary group
(b) Family, caste, race – In-Voluntary Industrial
(c) Dyad-triad, kin group – Small group
(d) Nation, State – Reference group
Answer:
(d) Nation, State – Large group
Question 2.
(a) Secondary Group – Large
(b) Primary Group – Small
(c) Reference Group – Mutual Co-operation
(d) Voluntary Group – Based on Choice
Answer:
(c) Reference Group – Guide our behaviour
![]()
Question 3.
(a) Different ways of wearing a sari – Folkways
(b) The Hindu Marriage Act, 1955 – Statutory law
(c) Tribal laws – Customary law
(d) Sexual relations before marriage are not permitted – Mores
Answer:
(b) The Hindu Marriage Act, 1955 – Enacted law
Question 4.
(a) Physical proximity – Primary group
(b) Indirect relations – Secondary relations
(c) Comparing oneself to – Reference group
(d) Membership based on choice – Involuntary group
Answer:
(d) Membership based on choice – Voluntary group
Question 5.
(a) ‘We Group’ – In-group
(b) Small in size – Small group
(c) ‘They Group’ – Primary group
(d) Large in size – Large group
Answer:
(c) ‘They-Group’ – Out group
Identify the appropriate term from the given options.
(Secondary Group, Ascribed Status, Role Conflict, Locality, Status, Social Group)
Question 1.
Occupation determined on the basis of caste.
Answer:
Ascribed Status
Question 2.
Formal, impersonal temporary relations.
Answer:
Secondary Group
Question 3.
A particular position, occupied by an individual in the society.
Answer:
Status
Question 4.
Difficulty of a working woman to pay attention to her sick baby and her at the same time.
Answer:
Role Conflict
Question 5.
It is the physical basis of community.
Answer:
Locality
Question 6.
Number of people with same goals and expectations.
Answer:
Social Group
Correct underlined words and complete the sentence.
Question 1.
Eating food with fork and spoon is an example of mores.
Answer:
Eating food with fork and spoon is an example of folkways.
![]()
Question 2.
When a person experiences difficulties in performing the duties it is called role conflict.
Answer:
When a person experiences difficulties in performing the duties it is called role strain.
Question 3.
Status determined on the basis of age, sex, caste, etc., are achieved status.
Answer:
Status determined on the basis of age, sex, caste, etc., are ascribed status.
Question 4.
In primary group the relations of members are formal in nature.
Answer:
In secondary group the relations of members are formal in nature.
Question 5.
Laws that are important and obligatory in nature are called customary law.
Answer:
Laws that are important and obligatory in nature are called enacted law.
Question 6.
Customs are more rigid than folkways.
Answer:
Mores are more rigid than folkways.
Question 7.
Locality means a shared sense of belonging.
Answer:
Community sentiment means a shared sense of belonging.
Write suitable examples of given concepts and justify your answer.
Question 1.
Achieved status in economic life.
Answer:
Example : An achieved status is something we accomplish in the course of our lives. To some extent, achieved status reflects our work and effort. College student, college dropout, CEO, doctors, athlete, professor are examples of achieved statuses.
It is attained by a person largely through her or his own effort. In achieved status, individuals or groups have the freedom to change their social status. Through this, social mobility is possible. On the basis of a person’s unique talent it is achieved. It appears in different fields in society such as politics, sports, education, and industry and helps an individual to change his economic status.
Question 2.
Role conflict as a student.
Answer:
Example : In today’s society, students have a lot of burden in addition to which, there are unsatisfying and unlimited wants of their parents. In today’s world, competition is so high that only the academic subjects are not enough and students have to prepare for other professional courses. In this manner a student has to play different roles by which they experience role conflict. Where two or more roles cannot be performed at the same time, it is called role conflict. Role conflict is the tension caused due to trying to balance two or more statuses.
Question 3.
Secondary group as a impersonal group.
Answer:
Example: Nation, political party and trades union, etc.
The secondary group refers to a formal, impersonal group. There is limited proximity and closeness among members in the secondary group. Persons in secondary groups may not be known to each other personally. Due to its large size, there is limited personal interaction. According to Horton and Hunt, ‘Secondary groups are goal-oriented’ and intentionally formed to fulfil the objectives of its members.
Question 4.
Enacted Law in a modern society.
Answer:
Example : The Hindu Marriage Act, 1955. The Domestic Violence Act, 2005.
This law is in a written form. It is important as well as obligatory in a modern, complex and dynamic society. It is applicable to all persons in that particular society.
![]()
Question 5.
Role set.
Answer:
Example : A university professor frequently gets involved in teaching, research, consultancy, administration, publishing, examining etc.
Role set also known as a role complex is a set of roles that centres around a particular social status.
Write short notes.
Question 1.
Elements of Community.
Answer:
A community is a territorial group. It always occupies some geographical area. It has its own definite territorial boundaries. Locality is the physical basis of community. The nomadic community also has locality though they have changing habitation.
1. Locality – A group of people form a community only when they begin to reside in a definite locality. Living together helps people to develop social contacts. Togetherness also gives people protection, safety and security. It helps members to fulfil their common interests.
Living together helps people to develop social contacts. Togetherness also gives people protection, safety and security. It helps members to fulfil their common interests.
2. Community Sentiment means a shared sense of belonging. Members must be aware of staying together and sharing common interests. People living in a community must have awareness of sharing a way of life. Due to this community sentiment, individuals are emotionally attached to their community.
Question 2.
Social Status and its types.
Answer:
1. Social status means the position in society. Ralph Linton has given two types of status on the basis of given status and achieved status. A person occupies different types of status at different place. For example, a parent at home may occupy the status of teacher in school, or as customer in a market and so no.
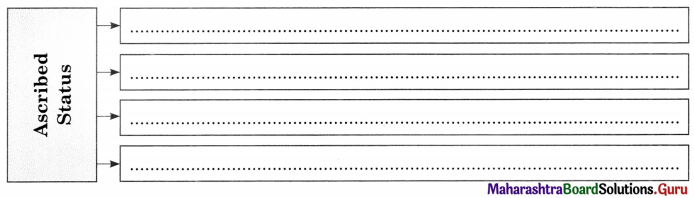
2. Ascribed status : It is assigned to a person by society. Generally, this assignment takes place at birth. It is determined on the basis of age, sex, kinship, race etc. These determinants are biological in origin but are significant mainly because of the social meanings that they have in our culture.
3. Achieved status : It is attained by a person largely through her or his own effort. On the basis of a person’s unique talent it is achieved. It appears in different fields in society such as politics, sports, education, and industry.
Question 3.
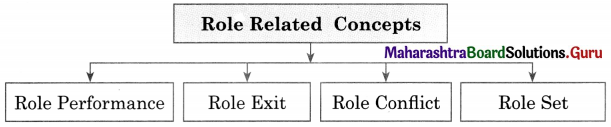
Social Role and related concepts.
Answer:
The functional aspect of status is known as ‘role’. It is also a behavioural aspect of duties which are associated with a status. When a person behaves in accordance with one’s position in society, it is termed as ‘role’.
- Role performance : The way a person actually plays one’s role in a situation.
- Role set : A set of roles (a role complex) that centres around a particular social status. For example, a University professor frequently gets involved in teaching, research, consultancy, administration, publishing, examining etc.
- Role strain : A feeling of difficulty or stress in fulfilling the demands of one’s role obligations.
- Role conflict: Incompatibility between two or more roles that an individual is expected to perform in a given situation. For example, the role of a working women, who also manages the home.
- Role exit: According to Helen Rose, role exit is a process of disengagement from a role that i is central to one’s self identity, in order to establish a new role and identity.
Characteristics of social group:
- A social group consists of two or more persons e.g., two friends, wife and husband.
- Social group is a system of social interaction.
- Group life involves mutual awareness.
- ‘We feeling’ promotes group unity.
- Groups are formed for the fulfilment of certain common interests, e.g., political groups, religious groups, caste groups, sports groups
- Each group has its own norms, rules to regulate behaviour of its members.
- Social groups are dynamic in nature, i.e. they change from time to time.
Differentiate between.
Question 1.
Role and Status.
Answer:
| Role | Status |
| (i) Role is defined as the function assumed or part played by a person or thing in a particular situation. | (i) Status is defined as the official classification given to a person, country or organisation, determining their rights or responsibilities. |
| (ii) A role is the part our society expects us to play in a given status. | (ii) Status is our relative social position within a group. |
| (iii) The person behaves in accordance with one’s position in the society. | (iii) The status of a person is known according to their prestige and power in society. |
| (iv) Roles are of different types, example, role strain, role conflict, role performance, etc. | (iv) Status are of two types, example, ascribed status and achieved status. |
Question 2.
Small Group and Large Group.
Answer:
| Small Group | Large Group |
| (i) Informal in nature and unpatterned. | (i) Formal in nature and patterned. |
| (ii) Based on informal nature of interaction. | (ii) Based on formal nature of interaction. |
| (iii) There is personal interaction. | (iii) Personal interaction is difficult. |
| (iv) Small in size. | (iv) Large in size. |
| (v) Examples – Family, Dyad-Triad, Kin group. | (v) Examples-Race, Nation, State, University. |
![]()
Question 3.
Ascribed Status and Achieved Status.
Answer:
| Ascribed Status | Achieved Status |
| (i) It is based on birth. | (i) Obtained on merit or effort by an individual. |
| (ii) Related with individual’s biological factors such as age, sex and kinship relations. | (ii) Individuals intelligence, skill, ambition, merit, effort are the bases of this status. |
| (iii) Absence of mobility as it is static in nature. | (iii) It is more mobile in nature. |
| (iv) Less significant in modern society. | (iv) More important in modern society. |
Explain the following concept with suitable examples.
Question 1.
Community
Answer:
1. The term community denotes uniformly and permanently shared lives of people over a region.
2. When a group of people live in a definite territory to fulfil their common objectives and needs we call it a community. Locality and community sentiments are two elements of community locality -A group of people form a community only when they begin to reside in a definite locality and community sentiment Community sentiment means a shared sense of belonging.
Example : Hindu community, Muslim community, Rural community, Tribal community, etc.
Question 2.
Social Norms
Answer:
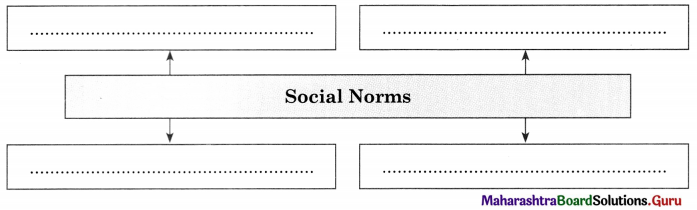
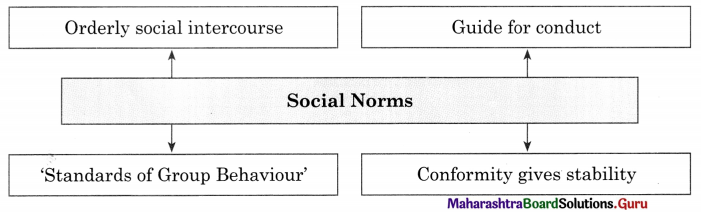
- They are generally known as standards of group behaviour.
- It is related to conformity in society. Conformity gives stability to society and creates peace and order in society.
- No society and no social group can exist without norms.
- Norms have made possible the orderly interaction of people in society.
- Everywhere, norms serve the individual as a guide for conduct.
- They are generally known as ‘standards of group behaviour.
- The word norm is used to represent folkways, mores, laws, customs etc.
Example : Obedience from children, the manner of speech, the time of meals, not telling lies etc.
Question 3.
In and out group
Answer:
- An in-group can be defined as any group or category to which people feel they belong.
- It compresses of everyone who is regarded as “we” or “us”.
- An out-group is a group or category to which people feel they do not belong.
- Out-group means “They group”. The very existence of an In-Group implies that there is an ‘Out-group’.
- Members of an in-group sometimes are threatened by another group, known as out group.
Example : In-group – Family, religion, race, gender we belong to.
Out-group – Race, culture, gender, age, religion, which we do not belong to.
Question 4.
Society
Answer:
(i) The society is the aggregate of people living together in a more or less ordered community. The most important component of society is social relationships among people.
(ii) For a relationship to be social, certain conditions must exist:
- The persons involved in the social relationship must be aware of each other.
- There must be some form of reciprocity between the individuals concerned. Society is dynamic as it changes continuously. Society includes likeness and differences
Example : Peoples Education Society, Ideal Housing society, Tribal society, Co-operative society, etc.
Complete the concept maps.
Question 1.
Answer:
Question 2.
Answer:
Question 3.

Answer:

![]()
Question 4.
Answer:
Question 5.
Answer:

Question 6.
| Types of group | |
| ‘We group’ | ——– |
| Membership based on choice | ——– |
| Membership based on birth | ——– |
| ‘They group’ | ——– |
| Dyad | ——– |
| Large in size | ——– |
| Intimate face to face relations | ——– |
| Distant relationship | ——– |
Answer:
| Types of group | |
| ‘We group’ | In-group |
| Membership based on choice | Voluntary group |
| Membership based on birth | Involuntary group |
| ‘They group’ | Out-group |
| Dyad | Small group |
| Large in size | Large group |
| Intimate face to face relations | Primary group |
| Distant relationship | secondary group |
Question 7.
Answer:
Question 8.

Answer:
State whether the following statements are true or false with reasons.
Question 1.
Society includes likeness and not differences.
Answer:
This statement is False.
Along with the likeness, society is also based on differences.
- Though the principle of likeness is essential for society as people have similarities with regard to their needs, aims, ideals, values, outlook towards life and so on, differences is an important factor for a healthy society.
- To satisfy different types of needs in society, different type of personalities are essential.
- These differences are based on sex, age, physical strength, intelligence, talent, personality and unequal possessions of material objects and wealth.
![]()
Question 2.
Primary groups are inclusive and permanent in nature.
Answer:
This statement is True.
- Physical proximity is essential for a primary group. Permanent close relations and smallness of the primary group create more solidarity among the members.
- The relationship in a primary group is not a means to fulfil any kind of objective and is based on emotional bonds.
- There is similarity of objectives, goals among the members of primary group which leads to group solidarity hence Primary groups are inclusive and permanent in nature
Question 3.
The relations of members of secondary group are informal in nature.
Answer:
This statement is False.
- The relations of members of secondary group are formal in nature. They are based on rules, laws, functioning etc.
- There is limited proximity and closeness among members in secondary groups.
- As a Special Interest Group’ secondary groups are intentionally formed to fulfil the objectives of its members.
- Persons in secondary groups may not be known to each other personally, it is goal oriented hence formal in nature.
Question 4.
Members of an in-group sometimes are threatened by another group
Answer:
This statement is True.
- Members of an in-group sometimes feel antagonistic to, or are threatened by another group, especially if the group is perceived as being different culturally or racially and are known as out group.
- An out-group consists of those persons towards whom we feel a sense of indifference, avoidance, disgust, competition or conflict.
- An ‘Out-Group’ is a group or category to which people feel they do not belong.
Give your personal response.
Question 1.
Do you think ascribed status is less significant in modern society?
Answer:
Yes, Ascribed status is less significant in modern society because it is determined on the basis of age, sex, kinship, race etc., which are biological in origin. It is static in nature hence lacks of mobility. Achieved status are more important in modern society which is attained by a person though his or her own effort. People with achieved status can improve their position within the social system on their own merit and achievements.
Answer the following in detail (About 150-200 words).
Question 1.
Explain the diverse nature of social groups by giving various classifications of groups with suitable examples.
Answer:
(i) In-Group and Out-Group : An In-Group can be defined as any group or category to which people feel they belong. It comprises everyone who is regarded as ‘we’ or ‘us’.
An Out-Group is a group or category to which people feel they do not belong. In-Group simply means ‘we group’ and Out-Group means ‘They-Group’. The members of an in-group identify themselves with one another and have a sense of belongingness to the group.
Example : One’s race, gender, favourite sports team, college. Members of an in-group sometimes feel antagonistic to, especially if the group is perceived as being different culturally or racially.
Example : Fans of opposing sports teams, people of different religion, race, caste etc.
(ii) Voluntary and Involuntary group : According to Charles Elwood voluntary group is a group in which membership is based on deliberate choice.
The members may join or resign from the said group.
Example : Political parties, trade unions, youth organisations, cultural associations etc.
An Involuntary Group is a group in which membership is based on birth or compulsion, rather than on choice.
Example : Groups like family, caste, religious group, race etc.
(iii) Small and Large Group : The term small group is used to refer to a group small enough for all members to interact simultaneously, and is informal in nature.
Example : Certain primary groups such as families.
Small groups include Dyad, Triad and other small groups. The smallest of all small social groups is the “Dyad” or two-member group.
Example : A married couple. Triad is a three member small group.
Example : When the married couple has their first child, the Dyad becomes a “Triad”.
Large Group is large in size and formal in nature.
Example : Nation, State, University.
![]()
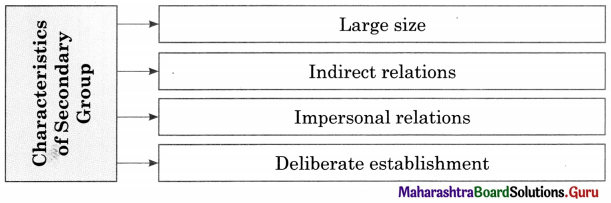
(iv) Primary and Secondary Group : The groups in which individuals work through mutual co-operation and are very closely related are called primary groups.
Example : Family, peer group, kin group, neighbourhood.
The secondary group refers to a formal, impersonal group, where mutual relations of persons are not very close.
Example : Political party, Nation, Commercial companies, Labour Union etc.