Bhagya

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 1 Rotational Dynamics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 1 Rotational Dynamics

Question 1.
What is circular motion?
Answer:
The motion of a particle along a complete circle or a part of it is called circular motion.

Question 2.
What is a radius vector in circular motion?
Answer:
For a particle performing circular motion, its position vector with respect to the centre of the circle is called the radius vector.
[Note : The radius vector has a constant magnitude, equal to the radius of the circle. However, its direction changes as the position of the particle changes along the circumference.]

Question 3.
What is the difference between rotation and revolution?
Answer:
There is no physical difference between them. It is just a question of usage. Circular motion of a body about an axis passing through the body is called rotation. Circular motion of a body around an axis outside the body is called revolution.

Question 4.
State the characteristics of circular motion.
Answer:

1. It is an accelerated motion : As the direction of velocity changes at every instant, it is an accelerated motion.
2. It is a periodic motion : During the motion, the particle repeats its path along the same trajectory. Thus, the motion is periodic.

Question 5.
Explain angular displacement in circular motion.
Answer:
The change in the angular position of a particle performing circular motion with respect to a reference line in the plane of motion of the particle and passing through the centre of the circle is called the angular displacement.

As the particle moves in its circular path, its angular position changes, say from θ₁ at time t to θ₂ at a short time δt later. In the interval δt, the position vector \(\vec{r}\) sweeps out an angle δθ = θ₂ – θ₁. δθ is the magnitude of the change in the angular position of the particle.

Infinitesimal angular displacement \(\overrightarrow{\delta \theta}\) in an infinitesimal time interval δt → 0, is given a direction perpendicular to the plane of revolution by the right hand thumb rule.

Question 6.
Explain angular velocity. State the right hand thumb rule for the direction of angular velocity.
Answer:
Angular velocity : The time rate of angular displacement of a particle performing circular motion is called the angular velocity.

1. If the particle has an angular displacement \(\delta \vec{\theta}\) in a short time interval δt, its angular velocity
   
2. \(\vec{\omega}\) is a vector along the axis of rotation, in the direction of \(d \vec{\theta}\), given by the right hand thumb rule.

Right hand thumb rule : If the fingers of the right hand are curled in the sense of revolution of the particle, then the outstretched thumb gives the direction of the angular displacement.

[Note : Angular speed, ω = |\(\vec{\omega}\)| = \(\frac{d \theta}{d t}\) is also called angular frequency. ]

Question 7.
Explain the linear velocity of a particle performing circular motion.
OR
Derive the relation between the linear velocity and the angular velocity of a particle performing circular motion.
Answer:
Consider a particle performing circular motion in an anticlockwise sense, along a circle of radius r. In a very small time interval δt, the particle moves from point A to point B through a distance δs and its angular position changes by δθ.

Since is tangential, the instantaneous linear velocity \(\vec{v}\) of a particle performing circular motion is along the tangent to the path, in the sense of motion of the particle.

\(\vec{v}\), \(\vec{\omega}\) and \(\vec{r}\) are mutually perpendicular, so that in magnitude, v = ωr.

Question 8.
State the relation between the linear velocity and the angular velocity of a particle in circular motion.
Answer:
Linear velocity, \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\) where ω is the angular velocity and r is the radius vector.

At every instant, \(\vec{v}\), \(\vec{\omega}\) and \(\vec{r}\) are mutually perpendicular, so that in magnitude v = ωr.

Question 9.
Define uniform circular motion (UCM).
Answer:
A particle is said to perform uniform circular motion if it moves in a circle or a circular arc at constant linear speed or constant angular velocity.

Question 10.
A stone tied to a string is rotated in a horizontal circle (nearly). If the string suddenly breaks, in which direction will the stone fly off ?
Answer:
In a circular motion, the instantaneous velocity \(\vec{v}\) is always tangential, in the sense of the motion. Hence, an inertial observer will see the stone fly off tangentially, in the direction of \(\vec{v}\) at the instant the string breaks.

Question 11.
What is the angular speed of a particle moving in a circle of radius r centimetres with a constant speed of v cm/s ?
Answer:
Angular speed, ω = \(\frac{v \mathrm{~cm} / \mathrm{s}}{r \mathrm{~cm}}\) = \(\frac{v}{r}\) rad/s.

Question 12.
Define the period and frequency of revolution of a particle performing uniform circular motion (UCM) and state expressions for them. Also state their SI units.
Answer:
(1) Period of revolution : The time taken by a particle performing UCM to complete one revolution is called the period of revolution or the period (T) of UCM.
T = \(\frac{2 \pi r}{v}\) = \(\frac{2 \pi}{\omega}\)
where v and ω are the linear and angular speeds, respectively.
SI unit: the second (s)
Dimensions : [M°L°T¹].

(2) Frequency of revolution : The number of revolutions per unit time made by a particle in UCM is called the frequency of revolution (f).

The particle completes 1 revolution in periodic time T. Therefore, it completes 1/T revolutions per unit time.
∴ Frequency f = \(\frac{1}{T}\) = \(\frac{v}{2 \pi r}\) = \(\frac{\omega}{2 \pi}\)
SI unit : the hertz (Hz), 1 Hz = 1 s^-1
Dimensions : [M°L°T^-1]

Question 13.
If the angular speed of a particle in UCM is 20π rad/s, what is the period of UCM of the particle?
Answer:
The period of UCM of the particle,
T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{20 \pi}\) = 0.1 s

Question 14.
Why is UCM called a periodic motion?
Answer:
In a uniform motion, a particle covers equal distances in equal intervals of time. Any motion which repeats itself in equal intervals of time is called a periodic motion. In a uniform circular motion (UCM), the particle takes the same time to complete each revolution, a distance equal to the circumference of the circle. Therefore, it is a periodic motion.

Question 15.
Give one example of uniform circular motion.
Answer:

1. Circular motion of every particle of the blades of a fan or the dryer drum of a washing machine when the fan or the drum is rotating with a constant angular speed.
2. Motion of the hands of a clock.
3. Motion of an Earth-satellite in a circular orbit.

Question 16.
What can you say about the angular speed of an hour hand as compared to that of the Earth’s rotation about its axis ?
Answer:
The periods of rotation of an hour hand and the Earth are T_h = 12 h and T_E = 24 h, respectively, so that their angular speeds are ω_h = \(\frac{2 \pi}{12}\) rad/h and ω_E = \(\frac{2 \pi}{24}\) rad/h.
∴ ω_h = 2ω_E

Question 17.
Explain the acceleration of a particle in UCM. State an expression for the acceleration.
Answer:
A particle in uniform circular motion (UCM) moves in a circle or circular arc at constant linear speed v. The instantaneous linear velocity \(\vec{v}\) of the particle is along the tangent to the path in the sense of motion of the particle. Since \(\vec{v}\) changes in direction, without change in its magnitude, there must be an acceleration that must be

1. perpendicular to \(\vec{v}\)
2. constant in magnitude
3. at every instant directed radially inward, i.e., towards the centre of the circular path.

Such a radially inward acceleration is called a centripetal acceleration.
∴ \(\vec{a}\) = \(\frac{d \vec{v}}{d t}\) = \(\overrightarrow{a_{\mathrm{r}}}\)

If \(\vec{\omega}\) is the constant angular velocity of the particle and r is the radius of the circle,
\(\overrightarrow{a_{\mathrm{r}}}\) = –\(\omega^{2} \vec{r}\)
where ω = |\(\vec{\omega}\)| and the minus sign shows that the direction of \(\vec{a}_{\mathrm{r}}\) is at every instant opposite to that of the radius vector \(\vec{r}\). In magnitude,
a_r = ω²r = \(\frac{v^{2}}{r}\) = ωv

[Note : The word centripetal comes from Latin for ‘centre-seeking’.]

Question 18.
Draw a diagram showing the linear velocity, angular velocity and radial acceleration of a particle performing circular motion with radius r.
Answer:

Question 19.
If a particle in UCM has linear speed 2 m/s and angular speed 5 rad/s, what is the magnitude of the centripetal acceleration of the particle ?
Answer:
The magnitude of the centripetal acceleration of the particle is a_r = ωv = (5)(2) = 10 m/s²

Question 20.
State any two quantities that are uniform in UCM.
Answer:
Linear speed and angular speed. (Also, kinetic energy, angular speed and angular momentum.)

Question 21.
State any two quantities that are nonuniform in UCM.
Answer:
Velocity and acceleration are nonuniform in UCM.
(Also, centripetal force.)

Question 22.
What is a nonuniform circular motion?
Answer:
Consider a particle moving in a plane along a circular path of constant radius. If the particle is speeding up or slowing down, its angular speed ω and linear speed v both change with time. Then, the particle is said to be in a non uniform circular motion.

Question 23.
Explain angular acceleration.
Answer:
Angular acceleration : The time rate of change of angular velocity of a particle performing circular motion is called the angular acceleration.

(i) If \(\delta \vec{\omega}\) is the change in angular Velocity in a short time interval St, the angular acceleration

(ii) The direction of \(\vec{\alpha}\) is the same as that of \(d \vec{\omega}\). We consider the case where a change in \(\vec{\omega}\) arises due to a change in its magnitude only. If the particle is speeding up, i.e., ω is increasing with time, then \(\vec{\alpha}\) is in the direction of \(\vec{\omega}\). If the particle is slowing down, i.e., ω is decreasing with time, then \(\vec{\alpha}\) is directed opposite to \(\vec{\omega}\).

(iii) If the angular speed changes from ω₁ to ω₂ in time f, the magnitude (α) of the average angular acceleration is
α = \(\frac{\omega_{2}-\omega_{1}}{t}\)

Question 24.
Explain the tangential acceleration of a particle in non uniform circular motion.
Answer:
Tangential acceleration : For a particle performing circular motion, the linear acceleration tangential to the path that produces a change in the linear speed of the particle is called the tangential acceleration.
Explanation :
(i) If a particle performing circular motion is speeding up or slowing down, its angular speed co and linear speed v both change with time.

The linear acceleration that produces a change only in the linear speed must be along \(\vec{v}\). Hence, it is called the tangential acceleration, \(\overrightarrow{a_{\mathrm{t}}}\). In magnitude, a_t = dv/dt

(ii) If the linear speed v of the particle is increasing, \(\overrightarrow{a_{\mathrm{t}}}\) is in the direction of \(\vec{v}\). If v is decreasing, \(\overrightarrow{a_{\mathrm{t}}}\) is directed opposite to \(\vec{v}\).

Question 25.
Obtain the relation between the magnitudes of the linear (tangential) acceleration and angular acceleration in non uniform circular motion.
Answer:
Consider a particle moving along a circular path of constant radius r. If the particle is speeding up or slowing down, its motion is nonuniform, and its angular speed ω and linear speed v both change with time. At any instant, v, ω and r are related by v = ωr
The angular acceleration of the particle is
α = \(\frac{d \omega}{d t}\)

The tangential acceleration \(\overrightarrow{a_{\mathrm{t}}}\) is the linear acceleration that produces a change in the linear speed of the particle and is tangent to the circle. In magnitude,

This is the required relation.

Question 26.
Obtain an expression for the acceleration of a particle performing circular motion. Explain its two components.
OR
For a particle performing uniform circular motion, \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\). Obtain an expression for the linear acceleration of a particle performing non-uniform circular motion.
OR
In circular motion, assuming \(\vec{v}\) = \(\vec{\omega}\) × \(\vec{r}\), obtain an expression for the resultant acceleration of a particle in terms of tangential and radial components.
Answer:
Consider a particle moving along a circular path of constant radius r. If its motion is nonuniform, then its angular speed ω and linear speed v both change with time.

acceleration is called the radial or centripetal acceleration \(\overrightarrow{a_{\mathrm{r}}}\).
\(\overrightarrow{a_{\mathrm{r}}}\) = \(\vec{\omega}\) × \(\vec{v}\) … (5)
In magnitude, a_r = ωv
since \(\vec{\omega}\) is perpendicular to \(\vec{v}\).
∴ \(\vec{a}\) = \(\overrightarrow{a_{\mathrm{t}}}\) + \(\overrightarrow{a_{\mathrm{r}}}\) …. (6)
This is the required expression.

Question 27.
What is the angle between linear acceleration and angular acceleration of a particle in nonuniform circular motion ?
Answer:
In a nonu niform circular motion, the angular acceleration is an axial vector, perpendicular to the plane of the motion. The linear acceleration is in the plane of the motion. Hence, the angle between them is 90°.

Question 28.
What are the differences between a nonuniform circular motion and a uniform circular motion? (Two points of distinction) Give examples.
Answer:
(i) Nonuniform circular motion :

1. The angular and tangential accelerations are non-zero, so that linear and angular speeds both change with time.
   
2. The net linear acceleration, being the resultant of the radial and tangential accelerations, is not radial, \(\vec{a}\) = \(\overrightarrow{a_{\mathrm{c}}}\) + \(\overrightarrow{a_{t}}\),
3. The magnitudes of the centripetal acceleration and the centripetal force are not constant.
4. Example : Motion of the tip of a fan blade when the fan is speeding up or slowing down.

(ii) Uniform circular motion :

1. The angular and tangential accelerations are zero, so that linear speed and angular velocity are constant.
2. The net linear acceleration is radially inward, i.e., centripetal.
3. The magnitudes of the centripetal acceleration and the centripetal force are also constant.
4. Example : Motion of the tips of the hands of a mechanical clock.

Question 29.
Write the kinematical equations for circular motion in analogy with linear motion.
Answer:
For circular motion of a particle with constant angular acceleration α,

where ω₀ and ω are the initial and final angular speeds, t is the time, ω_av the average angular speed and θ_o and θ the initial and final angular positions of the particle.

Then, the angular kinematical equations for the circular motion are (in analogy with linear kinematical equations for constant linear acceleration)
ω = ω₀ + αt
θ – θ₀ = ω₀t + \(\frac{1}{2} \alpha t^{2}\)
ω² = \(\omega_{0}^{2}\) + 2α (θ – θ₀)

Question 30.
Solve the following :

Question 1.
Certain stars are believed to be rotating at about 1 rot/s. If such a star has a diameter of 40 km, what is the linear speed of a point on the equator of the star?
Solution :
Data : d = 40 km, /= 1 rot/s
∴ r = \(\frac{d}{2}\) = \(\frac{40 \mathrm{~km}}{2}\) = 20 km = 2 × 10⁴ m
Linear speed, v = ωr = (2πf)r
= (2 × 3.142 × 1)(2 × 10⁴)
= 6.284 × 2 × 10⁴
= 1.257 × 10⁵ m/s (or 125.6 km/s)

Question 2.
A body of mass 100 grams is tied to one end of a string and revolved along a circular path in the horizontal plane. The radius of the circle is 50 cm. If the body revolves with a constant angular speed of 20 rad/s, find the

1. period of revolution
2. linear speed
3. centripetal acceleration of the body.

Solution :
Data : m = 100 g = 0.1 kg, r = 50 cm = 0.5 m, ω = 20 rad/s

1. The period of revolution of the body,
   
2. Linear speed, v = ωr = 20 × 0.5 = 10 m/s
3. Centripetal acceleration,
   a_c = w²r = (20)² × 0.5 = 200 m/s²

Question 3.
Calculate the angular speed of the Earth due to its spin (rotational motion).
Solution :
Data : T = 24 hours = 24 × 60 × 60 s

The angular speed of the Earth due to its spin (rotational motion) is 7.273 × 10^-5 rad/s.

Question 4.
Find the angular speed of rotation of the Earth so that bodies on the equator would feel no weight. [Radius of the Earth = 6400 km, g = 9.8 m/s²]
Solution :
Data : Radius of the Earth = r = 6400 km = 6.4 × 10⁶ m, g = 9.8 m/s²

As the Earth rotates, the bodies on the equator revolve in circles of radius r.

Question 31.
Write the kinematical equations for circular motion in analogy with linear motion.
Answer:
For circular motion of a particle with constant angular acceleration α,

where ω₀ and ω are the initial and final angular speeds, t is the time, ω_av the average angular speed and 0o and 0 the initial and final angular positions of the particle.

Then, the angular kinematical equations for the circular motion are (in analogy with linear kinematical equations for constant linear acceleration)
ω = ω₀ + αt
θ – θ_o = ω₀t + \(\frac{1}{2} \alpha t^{2}\)
ω² = \(\omega_{0}^{2}\) + 2α (θ – θ_o)

Question 32.
Solve the following :

Question 1.
Certain stars are believed to be rotating at about 1 rot/s. If such a star has a diameter of 40 km, what is the linear speed of a point on the equator of the star?
Solution :
Data : d = 40 km, f= 1 rot/s
∴ r = \(\frac{d}{2}\) = \(\frac{40 \mathrm{~km}}{2}\) = 20 km = 2 × 10⁴ m
Linear speed, v = ωr = (2πf)r
= (2 × 3.142 × 1)(2 × 10⁴)
= 6.284 × 2 × 10⁴
= 1.257 × 10⁵ m/s (or 125.6 km/s)

Question 2.
A body of mass 100 grams is tied to one end of a string and revolved along a circular path in the horizontal plane. The radius of the circle is 50 cm. If the body revolves with a constant angular speed of 20 rad/s, find the

1. period of revolution
2. linear speed
3. centripetal acceleration of the body.

Solution :
Data : m = 100 g = 0.1 kg, r = 50 cm = 0.5 m, ω = 20 rad/s

1. The period of revolution of the body,
   
2. Linear speed, v = ωr = 20 × 0.5 = 10 m/s
3. Centripetal acceleration,
   a_c = ω² = (20)² × 0.5 = 200 m/s²

Question 3.
Calculate the angular speed of the Earth due to its spin (rotational motion).
Solution :
Data : T = 24 hours = 24 × 60 × 60 s

The angular speed of the Earth due to its spin (rotational motion) is 7.273 × 10^-5 rad/s.

Question 4.
Find the angular speed of rotation of the Earth so that bodies on the equator would feel no weight. (Radius of the Earth = 6400 km, g = 9.8 m/s²]
Solution :
Data : Radius of the Earth = r = 6400 km
= 6.4 × 10⁶ m, g = 9.8 m/s²
As the Earth rotates, the bodies on the equator revolve in circles of radius r.
These bodies would not feel any weight if their centripetal acceleration (ωr) is equal to the acceleration due to gravity (g).
∴ ω²r = g
The angular speed of the Earth’s rotation,

Question 5.
To simulate the acceleration of large rockets, astronauts are seated in a chamber and revolved in a circle of radius 9.8 m. What angular speed is required to generate a centripetal acceleration 8 times the acceleration due to gravity? [g = 9.8 m/s²]
Solution :
Data : r = 9.8 m, g = 9.8 m/s², a = 8g
Centripetal acceleration = ω²r
∴ ω²r = 8g
∴ 9.8 ω² = 8(9.8)
∴ ω² = 8
The required angular speed, ω = \(\sqrt{8}\) = 2\(\sqrt{2}\) = 2.828 rad/s

Question 6.
The angular position of a rotating object is given by θ(t) = (1.55t² – 7.75 t + 2.87) rad, where t is measured in second.
(i) When is the object momentarily at rest ?
(ii) What is the magnitude of its angular acceleration at that time ?
Solution :

Question 7.
A motor part at a distance of 1.5 m from the motor’s axis of rotation has a constant angular acceleration of 0.25 rad/s². Find the magnitude of its linear acceleration at the instant when its angular speed is 0.5 rad/s.
Solution :
Data : r = 1.5 m, α = 0.25 rad/s², ω = 0.5 rad/s² a_r = ω²r = (0.5)²(1.5) = 0.25 × 1.5 = 0.375 m/s² a_t = αr = 0.25 × 1.5 = 0.375 m/s²
The linear acceleration,

Question 8.
A coin is placed on a stationary disc at a distance of 1 m from the disc’s centre. At time t = 0 s, the disc begins to rotate with a constant angular acceleration of 2 rad/s² around a fixed vertical axis through its centre and perpendicular to its plane.
Find the magnitude of the linear acceleration of the coin at t = 1.5 s. Assume the coin does not slip.
Solution :

Question 9.
A railway locomotive enters a stretch of track, which is in the form of a circular arc of radius 280 m, at 10 m/s and with its speed increasing uniformly. Ten seconds into the stretch its speed is 14m/s and at 18s its speed is 19 m/s. Find
(i) the magnitude of the locomotive’s linear acceleration when its speed is 14 m/s
(ii) the direction of this acceleration at that point with respect to the locomotive’s radial acceleration
(iii) the angular acceleration of the locomotive.
Answer:
Data : r = 280 m, v₁ = 10 m/s at t₁ = 0, v₂ = 14 m/s at t₂ = 10 s, v₃ = 19 m/s at t₃ = 18 s
(i) At t = t₂, the radial acceleration is

Since the tangential acceleration is constant, it may be found from the data for any two times.

(ii) If θ is the angle between the resultant linear acceleration and the radial acceleration,
tan θ = \(\frac{a_{\mathrm{t}}}{a_{\mathrm{r}}}\) = \(\frac{0.5}{0.7}\) = 0.7142
∴ θ = tan^-1 0.7142 = 35°32′

(iii) a_t = αr
The angular acceleration,
α = \(\frac{a_{\mathrm{t}}}{r}\) = \(\frac{0.5}{280}\)
= 1.785 × 10^-3 rad/s²
= 1.785 mrad/s²

Question 10.
The frequency of revolution of a particle performing circular motion changes from 60 rpm to 180 rpm in 20 seconds. Calculate the angular acceleration of the particle.
Solution :
Data : f₁ =60 rpm = \(\frac{60}{60}\) rev/s = 1 rev/s, f₂ = 180 rpm = \(\frac{180}{60}\) rev/s = 3 rev/s, t = 20 s
The angular acceleration in SI units,

OR
Using non SI units, the angular frequencies are ω₁ = 60 rpm = 1 rps and ω₂ = 180 rpm = 3 rps.

Question 11.
The frequency of rotation of a spinning top is 10 Hz. If it is brought to rest in 6.28 s, find the angular acceleration of a particle on its surface.
Solution:
Data: f₁ = 10Hz, f₂ = 0 Hz, t = 6.28s
The angular acceleration,

Question 12.
A wheel of diameter 40 cm starts from rest and attains a speed of 240 rpm in 4 minutes. Calculate its angular displacement in this time interval.
Solution:

Question 13.
A flywheel slows down uniformly from 1200 rpm to 600 rpm in 5 s. Find the number of revolutions made by the wheel in 5 s.
Solution :
Data : ω₀ = 1200 rpm, ω = 600 rpm, f = 5 s
Since the flywheel slows down uniformly, its angular acceleration is constant. Then, its average angular speed,

Its angular displacement in time t,
θ = ω_av.t = 15 × 5 = 75 revolutions

Question 33.
Define and explain centripetal force.
Answer:
Definition : In the uniform circular motion of a particle, the centripetal force is the force on the particle which at every instant points radially towards the centre of the circle and produces the centripetal acceleration to move the particle in its circular path.

Explanation : A uniform circular motion is an accelerated motion, with a radially inward (i.e., centripetal) acceleration –\(\frac{v^{2}}{r} \hat{\mathrm{r}}\) or \(-\frac{v^{2}}{r} \hat{\mathrm{r}}\), where \(\vec{r}\) is the radius vector and \(\hat{\mathbf{r}}\) is a unit vector in the direction of \(\vec{r}\). Hence, a net real force must act on the particle to produce this acceleration. This force, which at every instant must point radially towards the centre of the circle, is called the centripetal force. If m is the mass of the particle, the centripetal force is

Notes :

1. As viewed from an inertial frame of reference, the centripetal force is necessary and sufficient for the particle to perform UCM. At any instant, if the centripetal force suddenly vanishes, the particle would fly off in the direction of its linear velocity at that instant.
2. In case the angular or linear speed changes with time, as in nonuniform circular motion, the force is not purely centripetal but has a tangential component which accounts for the tangential acceleration.

Question 34.
Give any two examples of centripetal force.
Answer:
Examples of centripetal force :

1. For an Earth-satellite in a circular orbit, the centripetal force is the gravitational force exerted by the Earth on the satellite.
2. In the Bohr atom, the centripetal force on an electron in circular orbit around the nucleus is the attractive Coulomb force of the nucleus.
3. When an object tied at the end of a string is revolved in a horizontal circle, the centripetal force is the tension in the string.
4. When a car takes a turn in a circular arc on a horizontal road with constant speed, the force of static friction between the car tyres and road surfaces is the centripetal force.

Note : The tension in a string or the force of friction is electromagnetic in origin.

Question 35.
Define and explain centrifugal force.
Answer:
Definition : In the reference frame of a particle performing circular motion, centrifugal force is defined as a fictitious, radially outward force on the particle and is equal in magnitude to the particle’s mass times the centripetal acceleration of the reference frame, as measured from an inertial frame of reference.

Explanation : A uniform circular motion is an accelerated motion, with a centripetal acceleration of magnitude v²/r or ω²r. A frame of reference attached to the particle also has this acceleration and, therefore, is an accelerated or noninertial reference frame. The changing direction of the linear velocity appears in this reference frame as a tendency to move radially outward. This is explained by assuming a fictitious centrifugal, i.e., radially outward, force acting on the particle. Since the particle is stationary in its reference frame, the magnitude of the centrifugal force is mv²/r or mω²r, the same as that of the centripetal force on the particle.

Note : The word ‘centrifugal’ comes from the Latin for ‘fleeing from the centre’. The word has the same root fuge from the Latin ‘to flee’ as does refugee.

Question 36.
Give any two examples of centrifugal force.
Answer:
Examples of centrifugal force :

1. A person in a merry-go-round experiences a radially outward force.
2. Passengers of a car taking a turn on a level road experience a force radially away from the centre of the circular road.
3. A coin on a rotating turntable flies off for some high enough angular speed of the turntable.
4. As the Earth rotates about its axis, the centrifugal force on its particles is directed away from the axis. The force increases as one goes from the poles towards the equator. This leads to the bulging of the Earth at the equator.

Question 37.
Explain why centrifugal force is called a pseudo force.
Answer:
A force which arises from gravitational, electromagnetic or nuclear interaction between matter is called a real force. The centrifugal force does not arise due to any of these interactions. Therefore, it is not a real force.

The centrifugal force in the noninertial frame of reference of a particle in circular motion is the effect of the acceleration of the frame of reference. Therefore, it is called a pseudo or fictitious force.

Question 38.
Distinguish between centripetal force and centrifugal force. State any two points of distinction.
Answer:

Centripetal force	Centrifugal force
1. Centripetal force is the force required to provide centri­petal acceleration to a par­ticle to move it in a circular path.	1. The centrifugal tendency of the particle, in its acceler­ated, i.e., non-inertial, frame of reference, is explained by assuming a centrifugal force acting on it.
2. At every instant, it is directed radially towards the centre of the circular path.	2. At every instant, it is directed radially away from the centre of the circular path.
3. It is a real force arising from gravitational or electromag­netic interaction between matter.	3. It is a pseudo force since it is the effect of the acceleration of the reference frame of the revolving particle.

Question 39.
Solve the following :

Question 1.
An object of mass 0.5 kg is tied to a string and revolved in a horizontal circle of radius 1 m. If the breaking tension of the string is 50 N, what is the maximum speed the object can have?
Solution :
Data : m = 0.5 kg, r = 1 m, F = 50 N
The maximum centripetal force that can be applied is equal to the breaking tension.

This is the maximum speed the object can have.

Question 2.
A certain string 500 cm long breaks under a tension of 45 kg wt. An object of mass 100 g is attached to this string and whirled in a horizontal circle. Find the maximum number of revolutions that the object can make per second without breaking the string, [g = 9.8 m/s²]
Solution :
Data : m = 100 g = 0.1 kg, r = 500 cm = 5 m, g = 9.8 m/s², F = 45 kg wt = 45 × 9.8 N
The breaking tension is equal to the maximum centripetal force that can be applied.
∴ F = mω²r ,
But ω = 2πf, where/is the corresponding frequency of revolution.

The maximum number of revolutions per second, f = 4.726 Hz

Question 3.
A disc of radius 15 cm rotates with a speed of 33\(\frac{1}{3}\) rpm. Two coins are placed on it at 4 cm and 14 cm from its centre. If the coefficient of friction between the coins and the disc is 0.15, which of the two coins will revolve with the disc ?
Solution :
Data : r = 15 cm = 0.15 m,
f = 33\(\frac{1}{3}\) rpm = \(\frac{100}{3 \times 60}\)rev/s = \(\frac{5}{9}\) Hz, µ_s = 0.15, r₁ = 4 cm = 0.04 m, r₂ = 14 cm = 0.14 m

To revolve with the disc without slipping, the necessary centripetal force must be less than or equal to the limiting force of static friction.

Limiting force of static friction, f_s = µ_s N = µ_s (mg) where m is the mass of the coin and N = mg is the normal force on the coin.
∴ mω²r ≤ µ_s(mg) or ω²r ≤ µ_sg
µ_sg = 0.15 × 9.8 = 1.47 m/s²
For the first coin, r₁ = 0.04 m.
∴ ω²r₁ = (3.491)² × 0.04 = 12.19 × 0.04 = 0.4876 m/s²
Since, ω²r₁ < µ_sg, this coin will revolve with the disc. For the second coin, r₂ = 0.14 m.
∴ ω²r₂ = (3.491)² × 0.14 = 12.19 × 0.14 = 1.707 m/s²
Since, ω²r₂ > µ_sg, this coin will not revolve with the disc.
Thus, only the coin placed at 4 cm from the centre will revolve with the disc.

Question 40.
Derive an expression for the maximum safe speed for a vehicle on a horizontal circular road without skidding off. State its significance.
Answer:
Consider a car of mass m taking a turn of radius r along a level road. If µ_s is the coefficient of static friction between the car tyres and the road surface, the limiting force of friction is f_s = µ_sN = µ_smg where N = mg is the normal reaction. The forces on the car, as seen from an inertial frame of reference are shown in below figure.

Then, the maximum safe speed v_max with which the car can take the turn without skidding off is set by maximum centripetal force = limiting force of static friction

This is the required expression.
Significance : The above expression shows that the maximum safe speed depends critically upon friction which changes with circumstances, e.g., the nature of the surfaces and presence of oil or water on the road. If the friction is not sufficient to provide the necessary centripetal force, the vehicle is likely to skid off the road.

[Note : At a circular bend on a level railway track, the centrifugal tendency of the railway carriages causes the flange of the outer wheels to brush against the outer rail and exert an outward thrust on the rail. Then, the reaction of the outer rail on the wheel flange provides the necessary centripetal force.]

Question 41.
Derive an expression for the maximum safe speed for a vehicle on a circular horizontal road without toppling/overturning/rollover.
Answer:
Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are :

1. the lateral limiting force of static friction \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels-acting along the axis of the wheels and towards the centre of the circular path which provides the necessary centripetal force.
2. the weight \(m \vec{g}\) acting vertically downwards at the centre of gravity (C.G.)
3. the normal reaction \(\vec{N}\) of the road on the wheels, acting vertically upwards effectively at the C.G. Since maximum centripetal force = limiting force of static friction,
   

In a simplified rigid-body vehicle model, we consider only two parameters-the height h of the C.G. above the ground and the average distance b between the left and right wheels called the track width.

The friction force \(\overrightarrow{f_{\mathrm{s}}}\) on the wheels produces a torque T, that tends to overturn/rollover the car about the outer wheel. Rotation about the front-to-back axis is called roll

When the inner wheel just gets lifted above the ground, the normal reaction \(\vec{N}\) of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque \(\tau_{\mathrm{r}}\) which tends to restore the car back on all four wheels
\(\tau_{\mathrm{r}}\) = mg.\(\frac{b}{2}\) … (3)

The car does not topple as long as the restoring torque \(\tau_{\mathrm{r}}\) counterbalances the toppling torque \(\tau_{\mathrm{t}}\). Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by

Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force \(m \vec{g}\) passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower centre of gravity.

Question 42.
A carnival event known as a “well of death” consists of a large vertical cylinder inside which usually a stunt motorcyclist rides in horizontal circles. Show that the minimum speed necessary to keep the rider from falling is given by v = \(\sqrt{r g / \mu_{s}}\), in usual notations.
Answer:
The forces exerted on the rider are

1. the normal force \(\vec{N}\) exerted by the wall, directed radially inward, is the centripetal force,
2. the upward frictional force \(\overrightarrow{f_{\mathrm{s}}}\) exerted by the wall, since the motorcycle has a tendency to slide down,
3. the downward gravitational force \(m \vec{g}\).

which is the required expression.

Question 43.
A road at a bend should be banked for an optimum or most safe speed v₀. Derive an expression for the required angle of banking.
OR
Obtain an expression for the optimum or most safe speed with which a vehicle can be driven along a curved banked road. Hence show that the angle of banking is independent of the mass of a vehicle.
Answer:
Consider a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum or most safe speed v₀. Let m be the mass of the car. In general, the forces acting on the car are
(a) its weight \(m \vec{g}\), acting vertically down
(b) the normal reaction of the road \(\vec{N}\), perpendicular to the road surface
(c) the frictional force \(\overrightarrow{f_{s}}\) along the inclined surface of the road.

At the optimum speed, frictional force is not relied upon to contribute to the necessary lateral centripetal force. Thus, ignoring \(\overrightarrow{f_{\mathrm{s}}}\), resolve \(\vec{N}\) into two perpendicular components : N cos θ vertically up and N sin θ horizontally towards the centre of the circular path. Since there is no acceleration in the vertical direction, N cos θ balances mg and N sin θ provides the necessary centripetal force.

Equation (3) gives the expression for the required angle of banking. From EQ. (3), we can see that θ depends upon v₀, r and g. The angle of banking is independent of the mass of a vehicle negotiating the curve. Also, for a given r and θ, the recommended optimum speed is
v₀ = \(\sqrt{r g \tan \theta}\) … (4)

Question 44.
State any two factors on which the most safe speed of a car in motion along a banked road depends.
Answer:
The angle of banking of the road and the radius of the curved path.

Question 45.
A curved horizontal road must be banked at an angle θ’ for an optimum speed v. What will happen to a vehicle moving with a speed v along this road if the road is banked at an angle θ such that
(i) θ < θ’
(ii) θ > θ’?
Answer:
(i) For θ < θ’, the horizontal component of the normal reaction would be less than the optimum value and will not be able to provide the necessary centripetal force. Then, the vehicle will tend to skid outward, up the inclined road surface.

(ii) For θ > θ’, the horizontal component of the normal reaction would be more than the necessary centripetal force. Then, the vehicle will tend to skid down the banked road.

Question 46.
A banked circular road is designed for traffic moving at an optimum or most safe speed v₀. Obtain an expression for
(a) the minimum safe speed
(b) the maximum safe speed with which a vehicle can negotiate the curve without skidding.
Answer:
Consider a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum speed v. Let m be the mass of the car. In general, the forces acting on the car are
(a) its weight \(m \vec{g}\), acting vertically down
(b) the normal reaction of the road \(\vec{N}\), perpendicular to the road surface
(c) the frictional force \(\overrightarrow{f_{\mathrm{s}}}\) along the inclined surface of the road.
If µ_s is the coefficient of static friction between the tyres and road, f_s = µ_sN.

(a) For minimum safe speed : If the car is driven at a speed less than the optimum speed v₀, it may tend to slide down the inclined surface of the road so that \(\overrightarrow{f_{\mathrm{s}}}\) is up the incline.

Resolve \(\vec{N}\) and \(\overrightarrow{f_{\mathrm{s}}}\) into two perpendicular components : Ncos θ and f_s sin θ vertically up; N sin θ horizontally towards centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components N sin θ and f_s cos θ together provide the necessary centripetal force, and N cos θ balances the sum mg + f_s sin θ. If v_max is the maximum safe speed without skidding,

(b) For maximum safe speed : If the car is driven fast enough, at a speed greater than the optimum speed v, it may skid off up the incline so that \(\overrightarrow{f_{\mathrm{s}}}\) is down the incline.

Resolve \(\vec{N}\) and \(\overrightarrow{f_{\mathrm{s}}}\) into two perpendicular components : N cos θ vertically up and f_s sin θ vertically down; N sin θ and f_s cos θ horizontally towards the centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components N sin θ and f cos θ together provide the necessary centripetal force, and N cos θ balances the sum mg + f sin θ. If v is the maximum safe
speed without skidding,

Ignoring few special cases, the maximum value of µ_s = 1. Thus, for θ ≥ 45°, v_max = ∞, i.e., on a heavily banked road a car is unlikely to skid up the incline and the minimun limit is more important.

Question 47.
Solve the following :

Question 1.
Find the maximum speed with which a car can be safely driven along a curve of radius 100 m, if the coefficient of friction between its tyres and the road is 0.2 [g = 9.8 m/s²].
Solution :
Data : r = 100 m, µ_s = 0.2, g = 9.8 m/s²
The maximum speed, v = \(\sqrt{r \mu_{s} g}\)
= \(\sqrt{100 \times 0.2 \times 9.8}\) = 14 m/s

Question 2.
A flat curve on a highway has a radius of curvature 400 m. A car goes around the curve at a speed of 32 m/s. What is the minimum value of the coefficient of friction that will prevent the car from sliding?
Solution:
Data : r = 400 m, v = 32 m/s, g = 10 m/s²

Question 3.
A car can be driven on a flat circular road of radius r at a maximum speed v without skidding. The same car is now driven on another flat circular road of radius 2r on which the coefficient of friction between its tyres and the road is the same as on the first road. What is the maximum speed of the car on the second road such that it does not skid?
Solution:
Data: v₁ = v, r₁ = r, r₂ = 2r
On a flat circular road, the maximum safe speed is

Question 4.
On a dry day, the maximum safe speed at which a car can be driven on a curved horizontal road without skidding is 7 m/s. When the road is wet, the frictional force between the tyres and road reduces by 25%. How fast can the car safely take the turn on the wet road ?
Solution:
Let subscripts 1 and 2 denote the values of a quantity under dry and wet conditions, respectively.
Data : v₁ = 7 m/s, f₂ = f₁, – 0.25f₁ = 0.75f₁

On a dry horizontal curved road, the frictional force between the tyres and road is f₁ = µ₁mg, where m is the mass of the car and g is the gravitational acceleration.

The maximum safe speed for taking a turn of radius r on a dry horizontal curved road is

Question 5.
A coin kept at a distance of 5 cm from the centre of a turntable of radius 1.5 m just begins to slip when the turntable rotates at a speed of 90 rpm. Calculate the coefficient of static friction between the coin and the turntable. [g = π² m/s²]
Solution:
Data: r = 5 cm = 0.05 m, f = 90 rpm = \(\frac{90}{60}\) rps = 1.5 rps, g = π² m/s²

The centripetal force for the circular motion of the coin is provided by the friction between the coin and the turntable. The coin is just about to slip off the turntable when the limiting force of friction is equal to the centripetal force.

Question 6.
A thin cylindrical shell of inner radius 1.5 m rotates horizontally, about a vertical axis, at an angular speed ω. A wooden block rests against the inner surface and rotates with it. If the coefficient of static friction between block and surface is 0.3, how fast must the shell be rotating if the block is not to slip and fall ?

Solution :
Data : r = 1.5 m, µ_s = 0.3
The normal force \(\vec{N}\) of the shell on the block is the centripetal force which holds the block in place. \(\vec{N}\) determines the friction on the block, which in turn keeps it from sliding downward. If the block is not to slip, the friction force \(\overrightarrow{f_{\mathrm{s}}}\) must balance the weight \(m \vec{g}\) of the block.
∴ N = mω²r and f_s = μ_sN = mg
∴ μ_s(ω²r) = mg

This gives the required angular speed.

Question 7.
A motorcyclist rounds a curve of radius 25 m at 36 km/h. The combined mass of the motorcycle and the man is 150 kg.

1. What is the centripetal force exerted on the motorcyclist ?
2. What is the upward force exerted on the motorcyclist?

Solution :
Data : r = 25m, v = 36 km/h = 36 × \(\frac{5}{18}\)m/s = 10 m/s, m = 150 kg, g = 10 m/s²

1. Centripetal force, F = \(\frac{m v^{2}}{r}\) = \(\frac{150 \times(10)^{2}}{25}\) = 600 N
2. Upward force = normal reaction of the road surface = mg = 150 × 10 = 1500 N

Question 8.
A motorcyclist is describing a circle of radius 25 m at a speed of 5 m/s. Find his inclination with the vertical. What is the value of the coefficient of friction between the tyres and ground ?
Solution :
Data : v = 5 m/s, r = 25 m, g = 10 m/s²

Question 9.
A motor van weighing 4400 kg (i.e., a motor van of mass 4400 kg) rounds a level curve of radius 200 m on an unbanked road at 60 km/h. What should be the minimum value of the coefficient of friction to prevent skidding ? At what angle should the road be banked for this velocity?
Solution :
Data : m = 4400 kg, r = 200 m,
v = 60 km/h = 60 × \(\frac{5}{18}\)m/s = \(\frac{50}{3}\) m/s, g = 10 m/s²

[Note : In part (ii), v is to be taken as the optimum speed.]

Question 10.
An amusement park ride (known variously as the Rotor, the Turkish Twist and the Gravitron) consists of a large vertical cylinder that is spun about it axis fast enough such that the riders remain pinned against its inner wall. The floor drops away once the cylinder has attained its full rotational speed. The radius of the cylinder is R and the coefficient of static friction between a rider and the wall is μ_s.
(i) Show that the minimum angular speed necessary to keep a rider from falling is given by ω = \(\sqrt{g / \mu_{s} R} \text {. }\).
(ii) Obtain a numerical value for the frequency of rotation of the cylinder in rotations per minute if R =4 m and
µ_s = 0.4.
Solution:
Data: R = 4 m, µ_s = 0.4, g = 10 m/s²
The forces exerted on the rider, when the floor
drops away, are

1. the normal force \(\vec{N}\) exerted by the wall, directed radially inward, is the centripetal force
2. the upward frictional force \(\overrightarrow{f_{\mathrm{s}}}\) exerted by the wall
3. the downward gravitational force mg .

∴ N = mω²R and f_s = µ_sN = µ_s (mω²R) where m is the mass of the rider and ω is the angular speed of the Rotor cylinder. For the rider not to fall, \(\overrightarrow{f_{\mathrm{s}}}\) must balances \(m \vec{g}\).

This is the minimum angular speed necessary. Since ω = 2πf, the corresponding frequency of rotation of the cylinder is

Question 11.
The two rails of a broad-gauge railway track are 1.68 m apart. At a circular curve of radius 1.6 km, the outer rail is raised relative to the inner rail by 8.4 cm. Find the angle of banking of the track and the optimum speed of a train rounding the curve.
Solution :
Data : l = 1.68 m = 168 cm, r = 1.6 km = 1600 m, h = 8.4 cm, g = 10 m/s²

Question 12.
A metre gauge train is moving at 72 kmph along a curved railway track of radius of curvature 500 m. Find the elevation of the outer rail above the inner rail so that there is no side thrust on the outer rail.
Solution :
Data : r = 500 m, v = 72 kmph = 72 × \(\frac{5}{18}\) m/s = 20 m/s, g = 10 m/s², l = 1 m
tan θ = \(\frac{v^{2}}{r g}\)
= \(\frac{(20)^{2}}{500 \times 10}\) = 0.08
The required angle of banking,
θ = tan^-1 (0.08) = 4°4′
The elevation of the outer rail relative to the inner rail,
h = l sin θ
= (1)(sin 4°4′) = 0.0709 m = 7.09 cm

Question 13.
A circular race course track has a radius of 500 m and is banked at 10°. The coefficient of static friction between the tyres of a vehicle and the road surface is 0.25. Compute
(i) the maximum speed to avoid slipping
(ii) the optimum speed to avoid wear and tear of the tyres.
Solution :
Data : r = 500 m, θ = 10°, µ_s = 0.25, g = 9.8 m/s², tan 10° = 0.1763

(i) On the banked track, the maximum speed of the vehicle without slipping (skidding) is

(ii) The optimum speed of the vehicle on the track is

Question 48.
Define a conical pendulum.
Answer:
A conical pendulum is a small bob suspended from a string and set in UCM in a horizontal plane with the centre of its circular path below the point of suspension such that the string makes a constant angle θ with the vertical.
OR
A conical pendulum is a simple pendulum whose bob revolves in a horizontal circle with constant speed such that the string describes the surface of an imaginary right circular cone.

Question 49.
Derive an expression for the angular speed of the bob of a conical pendulum.
OR
Derive an expression for the frequency of revolution of the bob of a corical pendulum.
Answer:
Consider a conical pendulum of string length L with its bob of mass m performing UCM along a circular path of radius r.
At every instant of its motion, the bob is acted upon by its weight \(m \vec{g}\) and the tension \(\vec{F}\) in the string. If the constant angular speed of the bob is ω, the necessary horizontal centripetal force is F_c = mω²r

F_c is the resultant of the tension in the string and the weight. Resolve \(\vec{F}\) into components F cos θ vertically opposite to the weight of the bob and F sin θ horizontal. F cos θ balances the weight. F sin θ is the necessary centripetal force.
∴ F sin θ = mω²r … (1)
and F cos θ = mg … (2)

is the required expression for ω.
[Note : From Eq. (4), cos θ = g/ω²L. Therefore, as ω increases, cos θ decreases and θ increases.
If n is the frequency of revolution of the bob,

is the required expression for the frequency.

Question 50.
What will happen to the angular speed of a conical pendulum if its length is increased from 0.5 m to 2 m, keeping other conditions the same?
Answer:
The angular speed of the conical pendulum will become half the original angular speed.

Question 51.
Write an expression for the time period of a conical pendulum. State how the period depends on the various factors.
Answer:
If T is the time period of a conical pendulum of string length L which makes a constant angle θ with the vertical,
T = 2π\(\sqrt{\frac{L \cos \theta}{g}}\)
is the required expression
(Note: L cos θ = OC = h, where h is the axial height of the cone.
∴ T = 2π\(\sqrt{\frac{h}{g}}\)

where g is the acceleration due to gravity at the place.

From the above expression, we can see that

1. T ∝ \(\sqrt{L}\)
2. T ∝ \(\sqrt{\cos \theta}\) if θ increases, cos θ and T decrease
3. T ∝ \(\frac{1}{\sqrt{g}}/latex]
4. The period is independent of the mass of the bob.

Question 52.
Solve the following :

Question 1.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of a 1.5 m long string. If the string makes an angle of 30° with the vertical, compute its period.
Solution :
Data : L = 1.5 m, θ = 30°, g = 10 m/s²
The period of the conical pendulum,

Question 2.
A string of length 0.5 m carries a bob of mass 0. 1 kg at its end. If this is to be used as a conical pendulum of period 0.4πs, calculate the angle of inclination of the string with the vertical and the tension in the string.
Solution :
Data : L = 0.5m, m = 0.1 kg, T = 0.4πs, g = 10 m/s²

Question 3.
In a conical pendulum, a string of length 120 cm is fixed at a rigid support and carries a bob of mass 150 g at its free end. If the bob is revolved in a horizontal circle of radius 0.2m around a vertical axis, calculate the tension in the string. [g = 9.8 m/s²]
Solution:
Data : L = 120 cm = 1.2 m, m = 150 g = 0.15 kg,
r = 0.2 m, g = 9.8 m/s²

Question 4.
A stone of mass 1 kg, attached at the end of a 1 m long string, is whirled in a horizontal circle. If the string makes an angle of 30° with the vertical, calculate the centripetal force acting on the stone.
Solution :
Data : m = 1 kg, L = 1 m, θ = 30°, g = 10 m/s²

Question 53.
What is vertical circular motion? Comment on its two types.
Answer:
A body revolving in a vertical circle in the gravitational field of the Earth is said to perform vertical circular motion.

A vertical circular motion controlled only by gravity is a nonuniform circular motion because the linear speed of the body does not remain constant although the motion can be periodic.

In a controlled vertical circular motion, such as that a body attached to a rod, the linear speed of the body can be constant (including zero) so that such a motion can be uniform and periodic.

Question 54.
A body, tied to a string, performs circular motion in a vertical plane such that the tension in the string is zero at the highest point. What is the linear speed of the body at the

1. lowest position
2. highest position ?

Answer:

1. [latex]\sqrt{5 r g}\)
2. \(\sqrt{r g}\) in the usual notation.

Question 55.
A body, tied to a string, performs circular motion in a vertical plane such that the tension in the string is zero at the highest point. What is the angular speed of the body at the

1. highest position
2. lowest position ?

Answer:

1. \(\sqrt{g / r}\)
2. \(\sqrt{5 g / r}\) in the usual notation.

Question 56.
In a vertical circular motion controlled by gravity, derive an expression for the speed at an arbitrary position. Hence, show that the speed decreases while going up and increases while coming down.
OR
In a nonuniform vertical circular motion, derive expressions for the speed and tension/normal force at an arbitrary position.
OR
Show that a vertical circular motion controlled by gravity is a non uniform circular motion.
Answer:
Consider a small body of mass m tied to a string and revolved in a vertical circle of radius r. At every instant of its motion, the body is acted upon by its weight \(m \vec{g}\) and the tension \(\vec{T}\) in the string. At any instant, when the body is at the position P, let the string make an angle θ with the vertical, \(m \vec{g}\) is resolved into components, mg cos θ (radial) and mg sin θ (tangential).

At point P shown, the net force on the body towards the centre, T-mg cos θ, is the necessary centripetal force on the body. If v is its speed at P,


Let v₂ be the speed of the body at the lowest point B, which is the reference level for zero potential energy. Then, the body has only kinetic energy

As the body goes from B to P, it rises through a height h = r – r cos θ = r(1 – cos θ).
Total energy at P = KE + PE

Assuming that the total energy of the body is conserved, total energy at any point = total energy at the bottom.
Then, from Eqs. (2) and (3),

From the above expression, it can be seen that the linear speed v changes with θ. Thus, as θ increases, (while going up) cos θ decreases, 1 – cos θ increases, and v decreases. While coming down, θ decreases and v increases. Hence, a vertical circular motion controlled by gravity is a nonuniform circular motion.

Substituting for v² from Eq. (4) in Eq. (1),

Equation (6) is the expression for the tension in the string at any instant in terms of the speed at the lowest point.

Question 57.
A body at the end of a rod is revolved in a non-uniform vertical circular motion. Show that
(i) it must have a minimum speed 2\(\sqrt{g r}\) at the bottom
(ii) the difference in tensions in the rod at the highest and lowest positions is 6 mg.
Answer:
Consider a body of mass m attached to a rod and revolved in a vertical circle of radius r at a place where the acceleration due to gravity is g. We shall assume that the rod is not rigid so that the tension in the rod changes. As the rod is rotated in a nonuniform circular motion, the tension in the rod changes from a minimum value T₁ when the body is at the highest point to a maximum value T₂ when the body is at the bottom of the circle. At every instant, the body is acted upon by two forces, namely/its weight \(m \vec{g}\) and the tension \(\vec{T}\) in the string.

Question 58.
You may have seen in a circus a motorcyclist driving in vertical loops inside a hollow globe (sphere of death). Explain clearly why the motor-cyclist does not fall down when at the highest point of the chamber.
Answer:
A motorcyclist driving in vertical loops inside a hollow globe performs vertical circular motion. Suppose the mass of the motorcycle and motorcyclist is m and the radius of the chamber is r. At every instant of the motion, the motorcyclist is acted upon by the weight \(m \vec{g}\) and the normal reaction \(\vec{N}\).

At the highest point, let v₁ be the speed and \(\vec{N}_{1}\) the normal reaction. Here, both \(\vec{N}_{1}\) and \(m \vec{g}\) are parallel, vertically downward. Hence, the net force on the motorcyclist towards the centre O is N₁ + mg. If this force is able to provide the necessary centripetal force at the highest point, the motorcycle does not lose contact with the globe and fall down.

The minimum value of this force is found from the limiting case when N, just becomes zero and the weight alone provides the necessary centripetal force :
\(\frac{m v_{1}^{2}}{r}\) = mg
This requires that the motorcycle has a minimum speed at the highest point given by \(v_{1}^{2}\) = gr or v₁ = \(\sqrt{g r}\)

[Note : The ‘globe of death’ is a circus stunt in which stunt drivers ride motorcycles inside a mesh globe. Starting from small horizontal circles, they eventually perform revolutions along vertical circles. The linear speed is more for larger circles but angular speed is more for smaller circles as in conical pendulum.]

Question 59.
A car crosses over a bridge which is in the form of a convex arc with a uniform speed,
(i) State the expression for the normal reaction on the car.
OR
How does the normal reaction on the car vary with speed?
(ii) Hence show that the maximum speed with which the car can cross the bridge without losing contact with the road is equal to \(\sqrt{r g}\).
Answer:
Suppose a car of mass m, travelling with a uniform speed v, crosses over a bridge which is in the form of a convex arc of radius r.
(i) The forces acting on it at the highest point are as shown in below figure. Their resultant mg-N provides the centripetal force.

is the required expression. It shows that as v increases, N decreases.

(ii) Equation (1) shows that for g – \(\frac{v^{2}}{r}\) = 0, i.e., for centripetal acceleration equalling the gravitational acceleration, N = 0. That is, for \(\frac{v^{2}}{r}\) = g or v = \(\sqrt{r g}\), the
car just loses contact with the road. Therefore, this is the maximum speed with which a car can cross the bridge, irrespective of its mass.

[Data : Take g = 10 m/s² unless specified otherwise]

Question 60.
Solve the following :

Question 1.
An object of mass 1 kg tied to one end of a string of length 9 m is whirled in a vertical circle. What is the minimum speed required at the lowest position to complete the circle ? [g = 9.8 m/s²]
Solution :
Data : m = 1 kg, r = 9 m, g = 9.8 m/s²
The minimum speed of the object at the lowest position is

Question 2.
A stone of mass 5 kg, tied at one end of a rope of length 0.8 m, is whirled in a vertical circle. Find the minimum velocity at the highest point and at the midway point, [g = 9.8 m/s²]
Solution:
Data : m = 5 kg, r = l = 0.8 m, g = 9.8 m/s²

1. The minimum velocity of the stone at the highest point in its path,
   v = \(\sqrt{r g}\) = \(\sqrt{0.8 \times 9.8}\) = 2.8 m/s
2. The minimum velocity of the stone at the midway point in its path,
   v = \(\sqrt{3 r g}\) = \(\sqrt{3 \times 0.8 \times 9.8}\) = 4.85 m/s

Question 3.
A small body of mass 0.3 kg oscillates in a vertical plane with the help of a string 0.5 m long with a constant speed of 2 m/s. It makes an angle of 60° with the vertical. Calculate the tension in the string.
Solution :
Data : m = 0.3 kg, r = 0.5 m, v = 2 m/s, θ = 60°, g = 10 m/s²

Question 4.
A bucket of water is whirled in a vertical circle at an arm’s length. Find the minimum speed at the top so that no water spills out. Also find the corresponding angular speed. [Assume r = 0.75 m]
Solution :
Data : r = 0.75 m, g = 10 m/s²
At the highest point the minimum speed required is v = \(\sqrt{r g}\) = \(\sqrt{0.75 \times 10}\) = 2.738 m/s
The corresponding angular speed is 2.738
ω = \(\frac{v}{r}\) = \(\frac{2.738}{0.75}\) = 3.651 rad/s

Question 5.
A pendulum, with a bob of mass m and string length l, is held in the horizontal position and then released into a vertical circle. Show that at the lowest position the velocity of the bob is \(\sqrt{2 g l}\) and the tension in the string is 3 mg.
Solution :
Taking the reference level for zero potential energy to be the bottom of the vertical circle, the initial potential energy of the bob at the horizontal position = mgh = mgl.

Hence, at the bottom where the speed of the bob is v, it has only kinetic energy = \(\frac{1}{2}\)mv².

This gives the required velocity at the lowest position.
Also, at the bottom, the tension (T) and the centripetal acceleration are upward while the force of gravity is downward.

Equations (1) and (2) give the required expressions for the velocity and tension at the lowest position.

Question 6.
A stone of mass 100 g attached to a string of length 50 cm is whirled in a vertical circle by giving it a velocity of 7 m/s at the lowest point. Find the velocity at the highest point.
Solution :
Data : m = 0.1 kg, r = l = 0.5 m, v₂ = 7 m/s, g = 10 m/s²
The total energy at the bottom, E_bot
= KE + PE = \(\frac{1}{2} m v_{2}^{2}\) + 0 = \(\frac{1}{2}\)(0.1) (7)² = 2.45 J
The total energy at the top, E_top = KE + PE = \(\frac{1}{2} m v_{1}^{2}\) + mg (2r)
= \(\frac{1}{2}\)(0.1)\(v_{1}^{2}\) + (0.1) (10) (2 × 0.5)
= 0.05\(v_{1}^{2}\) + 1
By the principle of conservation of energy,

Question 7.
A pilot of mass 50 kg in a jet aircraft executes a “loop-the-loop” manoeuvre at a constant speed of 250 m/s. If the radius of the vertical circle is 5 km, compute the force exerted by the seat on the pilot at
(i) the top of the loop
(ii) the bottom of the loop.
Solution :
Data: m = 50 kg, v = 250m/s, r = 5 km = 5 × 10³ m, g = 10 m/s²

(i) At the top of the loop : The forces on the pilot are the gravitational force \(m \vec{g}\) and the normal force \(\vec{N}_{1}\), exerted by the seat, both acting downward. So the net force downward that causes the centripetal acceleration has a magnitude

(ii) At the bottom of the loop : The forces on the pilot are the downward gravitational force \(m \vec{g}\) and the upward normal force \(\vec{N}_{2}\) exerted by the seat. So the net upward force that causes the centripetal acceleration has a magnitude N₂ – mg.

The forces exerted by the seat on the pilot at the top and bottom of the loop are 125 N and 1125 N, respectively.

Question 8.
A ball released from a height h along an incline, slides along a circular track of radius R (at the end of the incline) without falling vertically downwards. Show that h_min = \(\frac{5}{2}\) R.
Solution:
To just loop-the-loop, the ball must have a speed v₂ = \(\sqrt{5 R g}\) at the bottom of the circular track.

If h_min is the minimum height above the bottom of the circular track from which the ball must be released, by the principle of conservation of energy, we have,
mgh_min = \(\frac{1}{2} m v_{2}^{2}\) = \(\frac{1}{2} m(5 R g)\)

Note : 1f the ball rolls all along the track without slipping, its total energy at the top of the circular track should take into account the rotational kinetic energy of the ball.

Question 9.
A block of mass 1 kg is released from P on a frictionless track which ends with a vertical quarter circular turn.

What are the magnitudes of the radial acceleration and total acceleration of the block when it arrives at Q ?
Solution :
Data : m = 1 kg, h = 6 m, r = 2 m, g = 10 m/s²
Let v be the speed of the block at Question Then, the total energy of the block at Q is
E = KE + PE = \(\frac{1}{2} m v^{2}\) + mgr
By the principle of conservation of energy,

The radial acceleration has a magnitude 40 m/s². The total acceleration has a magnitude 41.23 m/s² and makes an angle of 14°2′ with the radial acceleration.

Question 10.
A loop-the-loop cart runs down an incline into a vertical circular track of radius 3 m and then describes a complete circle. Find the minimum height above the top of the circular track from which the cart must be released.
Solution :

Data : r = 3 m
To just loop-the-loop, the cart must have a speed V₁ = \(\sqrt{r g}\) at the top of the loop.

If h is the minimum height above the top of the loop from which the cart must be released, by the principle of conservation of energy, we have, mgh = \(\frac{1}{2} m v_{1}^{2}\) = \(\frac{1}{2} m g r\)
∴ h = \(\frac{r}{2}\) = \(\frac{3}{2}\) = 1.5 m

Question 11.
A motorcyclist rides in vertical circles in a hollow sphere of radius 5 m. Find the required minimum speed and minimum angular speed, so that he does not lose contact with the sphere at the highest point. [g = 9.8 m/s²]
Solution :
Data : r = 5 m, g = 9.8 m/s²
Let v and ω be respectively the required minimum speed and angular speed at the highest point.

Question 12.
The vertical section of a road over a bridge in the direction of its length is in the form of an arc of a circle of radius 4.4 m. Find the maximum speed with which a vehicle can cross the bridge without losing contact with the road at the highest point, if the centre of gravity of the vehicle is 0.5 m from the ground.
Solution :
Data: While travelling along the bridge, the vehicle moves along a vertical circle of radius r = 4.4 + 0.5 = 4.9 m, g = 10 m/s².
If m is the mass and v is the maximum speed of the vehicle, then at the highest point,

Question 13.
A small body tied to a string is revolved in a vertical circle of radius r such that its speed at the top of the circle is \(\sqrt{2 g r}\). Find
(i) the angular position of the string when the tension in the string is numerically equal to 5 times the weight of the body.
(ii) the KE of the body at this position
(iii) the minimum and maximum KEs of the body.
[Take m = 0.1 kg, r = 1.2 m, g = 10 m/s²]
Solution :
Data : v_top = \(\sqrt{2 g r}\), T = 5 mg, m = 0.1 kg, r = 1.2 m, g = 10 m/s²

Let the angular position of the string, θ = 0° when the body is at the bottom of the circle.

We assume total energy to be conserved and take the reference level for zero potential energy to be the bottom of the circle.

Total energy at the top, E

At P, the vertical displacement of the body from the bottom is r(1 – cos θ). Its total energy there is also E.

Question 14.
An object of mass 0.5 kg attached to a rod of length 0.5 m is whirled in a vertical circle at a constant angular speed. If the maximum tension in the rod is 5 kg wt, calculate the linear speed of the object and the maximum number of revolutions it can complete in a minute.
Solution :
Data : m = 0.5 kg, r = l = 0.5 m, g = 10 m/s²,
T₂ = 5 kg wt = 5 × 10 N

As the rod is rotated in a vertical circle at a constant angular speed, the linear speed of the object at the end of the rod is constant, say v. However, the tension in the rod changes from a minimum value T₁ when the object is at the highest point to a maximum value T₂ when the object is at the bottom of the circle.

At the bottom of the circle, the tension and acceleration are upward while the force of gravity is downward.

∴ The maximum number of revolutions the object can complete in a minute is 127.98.

Question 15.
A small body of mass m = 0.1 kg at the end of a cord 1 m long swings in a vertical circle. Its speed is 2 mIs when the cord makes an angle θ = 30° with the vertical. Find the tension in the cord.
Solution:
Data: m = 0.1 kg, r = 1 m, y = 2 m/s, θ = 30°,
g = 9.8 m/s²
When the cord makes an angle θ with the vertical, the centripetal force on the body is

Question 16.
A bucket of water is tied to one end of a rope 8 m long and rotated about the other end in a vertical circle. Find the number of revolutions per minute such that water does not spill.
Solution:
[Important note : The circular motion of the bucket in a vertical plane under gravity is not a uniform circular motion. Assuming the critical case of the motion such that the bucket has the minimum speed at the highest point required for the water to stay put in the bucket, we can find the minimum frequency of revolution. ]
Data :r = 8m, g = 9.8 m/s², π = 3.142
Assuming the bucket has a minimum speed v = \(\sqrt{r g}\) at the highest point, the corresponding angular speed is

Question 61.
Derive an expression for the kinetic energy of a body rotating with constant angular velocity.
Answer:
Consider a rigid body rotating with a constant angular velocity \(\vec{\omega}\) about an axis passing through the point O and perpendicular to the plane of the figure. Suppose that the body is made up of N particles of masses m₁, m₂, …, m_N situated at perpendicular distances r₁, r₂, , r_N, respectively, from the axis of rotation as shown in below figure.

As the body rotates, all the particles perform uniform circular motion with the same angular velocity \(\vec{\omega}\). However, they have different linear speeds depending upon their distances from the axis of rotation.

The linear speed of the particle with mass ml is v₁ = r₁ω. Therefore, its kinetic energy is

where I = \(\sum_{i=1}^{N} m_{i} r_{i}^{2}\) is the moment of inertia of the body about the axis of rotation.
Equation (2) gives the required expression.

Question 62.
Define moment of inertia. State the factors which it depends on. Obtain its dimensions and state its SI unit.
OR
Define moment of inertia. State its dimensions and SI units.
Answer:
(1) Moment of inertia : The moment of inertia of a body about a given axis of rotation is defined as the sum of the products of the masses of the particles of the body and the squares of their respective distances from the axis of rotation.

If the body is made up of N discrete particles of masses m₁, m₂, …,m_N situated at respective distances r₁, r₂, …, r_N from the axis of rotation, the moment of inertia of the body is

For a rigid body, having a continuous and uniform distribution of mass, the moment of inertia is
I = \(\int r^{2} d m\) …(2)
where dm is the mass of an infinitesimal element, situated at distance r from the axis of rotation.

(2) The moment of inertia of a rigid body depends on

1. the mass and shape of the body
2. orientation and position of the rotation axis
3. distribution of the mass about the rotation axis.

(3) Dimensions :
[Moment of inertia] = [mass] [distance]²
= [M] [L²] = [M¹L²T⁰]

(4) SI unit : The kilogram-metre² (kg.m²).

Question 63.
Explain the physical significance of moment of inertia.
Answer:
(1) The physical significance of moment of inertia can be understood by comparing the formulae in the following table.

Linear motion	Rotational motion
1. Momentum = mass × velocity	1. Angular momentum = moment of inertia × angular velocity
2. Force = mass × acceleration	2. Torque = moment of inertia × angular acceleration
3. Kinetic energy = \(\frac{1}{2} M v^{2}\)	3. Kinetic energy = \(\frac{1}{2} I \omega^{2}\)

(2) Force produces acceleration, while torque produces angular acceleration. Force and torque are analogous quantities. Also, momentum and angular momentum are analogous quantities.
(3) By comparing the above formulae, we find that moment of inertia plays the same role in rotational motion as that played by mass in linear motion. The moment of inertia of a body is its rotational inertia, that which opposes any tendency to change its angular velocity. In the absence of a net torque, the body continues to rotate with a uniform angular velocity.

Question 64.
Three point masses M₁, M₂ and M₃ are located at the vertices of an equilateral triangle of side a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through M₁ ?
Answer:

The moment of inertia of the system about the altitude passing through M₁ is

Question 65.
Find the moment of inertia of a hydrogen molecule about its centre of mass if the mass of each hydrogen atom is m and the distance between them is R.
Answer:
We assume the rotation axis to be a transverse axis through the centre of mass of the linear molecule H₂. Then, each of the hydrogen atom is a distance \(\frac{1}{2}\)R from the CM. Therefore, the MI of the molecule about this axis,

Notes :

1. For a H₂ molecule, mH = 1.674 × 10^-27 kg and bond length = 7.774 × 10^-11 m, so that I = 5.065 × 10^-48 kg.m².
2. As atoms are treated as particles, we do not consider rotation about the line passing through the atoms.

Question 66.
Solve the following :

Question 1.
Four particles of masses 0.2 kg, 0.3 kg, 0.4 kg and 0.5 kg respectively are kept at comers A, B, C and D of a square ABCD of side 1 m. Find the moment of inertia of the system about an axis passing through point A and perpendicular to the plane of the square.
Solution :
Data : m₁ = 0.2 kg, m₂ = 0.3 kg, m₃ = 0.4 kg, m₄ = 0.5 kg

The axis of rotation passes through point A and is perpendicular to the plane of the square. Hence the distance (r₁) of mass ml from the axis is r₁ =0, that of mass m₂ is r₂ = AB = 1 m, that of mass m₃ is r₃ = \(\sqrt{2}\)AC m and that of mass m₄ is r₄ = AD = 1 m.
The moment of inertia,

Question 2.
The moment of inertia of the Earth about its axis of rotation is 9.83 × 10 kg.m² and its angular speed is 7.27 × 10^-5 rad/s. Calculate its
(i) kinetic energy of rotation
(ii) radius of gyration. [ Mass of the Earth = 6 × 10²⁴ kg]
Solution :
Data : I = 9.83 × 10³⁷ kg.m², ω = 7.27 × 10^-5 rad/s, M = 6 × 10²⁴ kg

(i) The kinetic energy of rotation of the Earth,

Question 67.
State an expression for the moment of inertia of a thin ring about its transverse symmetry axis.
Answer:
A thin uniform ring (or hoop) has all its mass uniformly distributed along the circumference of a circle. It is taken to be a two-dimensional body. It is also assumed that the radial thickness of the ring is so small as to be completely negligible in comparison to its radius.

Consider a thin ring (or hoop) of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM).

The MI of the ring about the transverse symmetry axis is
I_CM = MR²

Question 68.
Derive an expression for the moment of inertia of a thin uniform disc about its transverse symmetry axis.
Answer:
A thin uniform disc has all its mass homogeneously distributed over its circular surface area. It is taken to be a two-dimensional body, i.e., its axial thickness is small as to be completely negligible in comparison to its radius. Consider a thin disc of radius R and mass M. Its mass per unit area is

The axis of rotation is the transverse symmetry axis, through its centre of mass (CM) and perpendicular to its plane. For rotation about this axis, we consider the disc to consist of a large number of thin concentric rings, having the same rotation axis as the transverse symmetry axis of the disc. One such elemental ring at a distance r from the rotation axis shown in below figure, has mass dm and radial width dr.

Since the disc is uniform, the area and mass of this elemental ring are

and its moment of inertia (MI) about the given axis is dm.r².
Therefore, the MI of the disc is

This gives the required expression.

Question 69.
Is radius of gyration of a rigid body a constant quantity?
Answer:
Radius of gyration of a rigid body depends on the distribution of mass of the body about a rotation axis and, therefore, changes with the choice of the rotation axis. Hence, unlike the mass of the body which is constant, radius of gyration and moment of inertia of the body are not constant.

Question 70.
State an expression for the radius of gyration of
(i) a thin ring
(ii) a thin disc, about respective transverse symmetry axis.
OR
Show that for rotation about respective transverse symmetry axis, the radius of gyration of a thin disc is less than that of a thin ring.
Answer:
(i) The MI of the ring about the transverse symmetry axis is
I_CM = MR² … (1)
Radius of gyration : The radius of gyration of the ring about the transverse symmetry axis is
K = \(\sqrt{I_{\mathrm{CM}} / M}\) = \(\sqrt{R^{2}}\) = R …… (2)

(ii) The MI of the disc about the transverse symmetry axis is
I_CM = \(\frac{1}{2}\)MR<² … (3)
Radius of gyration : The radius of gyration of the disc for the given rotation axis is

Question 71.
State and prove the theorem of parallel axis.
Answer:
Theorem of parallel axis : The moment of inertia of a body about an axis is equal to the sum of

1. its moment of inertia about a parallel axis through its centre of mass and
2. the product of the mass of the body and the square of the distance between the two axes.

Proof : Let I_CM be the moment of inertia (MI) of a body of mass M about an axis through its centre of mass C, and I be its MI about a parallel axis through any point O. Let h be the distance between the two axes.

Consider an infinitesimal mass element dm of the body at a point P. It is at a perpendicular distance CP from the rotation axis through C and a perpendicular distance OP from the parallel axis through O. The MI of the element about the axis through C is CP²dm. Therefore, the MI of the body about the axis through the CM is I_CM = \(\int \mathrm{CP}^{2} d m\). Similarly, the MI of the body about the parallel axis through O is I = \(\int \mathrm{OP}^{2} d m\).

∴ I = I_CM + Mh²
This proves the theorem of parallel axis.

Question 72.
State and prove the theorem of perpendicular axes about moment of inertia.
Answer:
Theorem of perpendicular axes : The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two mutually perpendicular axes in its plane and through the point of intersection of the perpendicular axis and the lamina.

Proof : Let Ox and Oy be two perpendicular axes in the plane of the lamina and Oz, an axis perpendicular to its plane. Consider an infinitesimal mass element dm of the lamina at the point P(Y, y). MI of the lamina about the z-axis, I_z = \(\int \mathrm{OP}^{2} d m\)

The element is at perpendicular distance y and x from the x- and y- axes respectively. Hence, the moments of inertia of the lamina about the x- and y-axes are, respectively,

This proves the theorem of perpendicular axes.

Question 73.
About which axis of rotation is the radius of gyration of a body the least ?
Answer:
The radius of gyration of a body is the least about an axis through the centre of mass (CM) of the body.

From the parallel axis theorem, we know that a given body has the smallest possible moment of inertia about an axis through its CM. The radius of gyration of a body about a given axis is directly proportional to the square root of its moment of inertia about that axis. Hence, the conclusion.
{OR I = I_CM + Mh². ∴ Mk² = \([/latexM k_{\mathrm{CM}}^{2}] + Mh².
∴ k² = [latex]k_{\mathrm{CM}}^{2}\) + h², which shows that k is minimum, equal to k_CM when h = 0.}

Question 74.
State an expression for the moment of inertia of a thin uniform rod about an axis through its centre and perpendicular to its length. Hence deduce the expression for its moment of inertia about an axis through its one end and perpendicular to its length.
OR
State an expression for the moment of inertia of a thin uniform rod about its transverse symmetry axis. Hence, deduce the expression for its moment of inertia about a parallel axis through one end. Also deduce the expressions for the corresponding radii of gyration.
Answer:
(1) MI about a transverse axis through centre : Consider a thin uniform rod AB of mass M and length L, rotating about a transverse axis through its centre C. C is also its centre of mass (CM).

(2) MI about a transverse axis through one end : Let I be its MI about a transverse axis through its end A. By the theorem of parallel axis,
I = I_CM + Mh² … (2)
In this case,

(3) Radii of gyration : The radius of gyration of the rod about its transverse symmetry axis is

The radius of gyration of the rod about the transverse axis through an end is

Question 75.
State the expression for the MI of a thin spherical shell (i.e., a thin-walled hollow sphere) about its diameter. Hence obtain the expression for its MI about a tangent.
Answer:
Consider a uniform, thin-walled hollow sphere radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass. The MI of the thin spherical shell about its diameter is
I_CM = \(\frac{2}{3}\)MR²

Let I be its MI about a tangent parallel to the diameter. Here, h = R = distance between the two axes. Then, according to the theorem of parallel axis,

Question 76.
Calculate the moment of inertia by direct integration of a thin uniform rod of mass M and length L about an axis perpendicular to the rod and passing through the ród at L/3, as shown below.
Check your answer with the parallel-axis theorem.

Answer:
Method of direct integration : Consider a thin uniform rod of mass M and length L. The axis of rotation is perpendicular to the rod and passing through the rod at L/3. We consider the origin of coordinates to be at this point and the x-axis to be along the rod,

Since the mass density is constant, the linear mass density is
λ = M/L
An element of the rod has mass dm and length dl = dx.

If the distance of each mass element from the axis is given by the variable x, the moment of inertia of an element about the axis of rotation is dI = x²dm
Since the rod extends from x= – L/3 to x = 2L/3, the MI of the rod about the axis is

Method of parallel-axis : The MI of the thin rod about a transverse axis through its CM is
I_CM = \(\frac{1}{12} M L^{2}\)
The given axis of rotation is at a distance h = \(\frac{L}{2}\) – \(\frac{L}{3}\) = \(\frac{L}{6}\) from the transverse symmetry axis.
Therefore, the MI of the rod about the given axis is

the same as arrived at by direct integration method.

Question 77.
State an expression for the moment of inertia of a thin ring about its transverse symmetry axis. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane. Also deduce the expressions for the corresponding radius of gyration.
Answer:
(1) MI about the transverse symmetry axis : Consider a thin ring (or hoop) of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM). It is assumed that the radial thickness of the ring is so small as to be completely negligible in comparison to radius R.

The MI of the ring about the transverse symmetry axis is
I_CM = MR² …(1)
Radius of gyration : The radius of gyration of the ring about the transverse symmetry axis is
k = \(\sqrt{I_{\mathrm{CM}} / M}\) = \(\sqrt{R^{2}}\) = R …(2)

(2) MI about a tangent perpendicular to its plane : Let I be its MI about a parallel axis, tangent to the ring. Here, h = R = distance between the two axes.
By the theorem of parallel axis,
I = I_CM + Mh² … (3)
= MR² + MR² = 2MR² …(4)
Radius of gyration : The radius of gyration of the ring about a transverse tangent is
k = \(\sqrt{I / M}\) = \(\sqrt{2 R^{2}}\) = \(\sqrt{2} R\) …(5)

Question 78.
Assuming the expression for the moment of inertia of a ring about its transverse symmetry axis, obtain the expression for its moment of inertia about
(1) a diameter
(2) a tangential axis in its plane. Also deduce the expressions for the corresponding radii of gyration.
Answer:
Let M be the mass of a thin ring of radius R. Let /CM be the moment of inertia (MI) of the ring about its transverse symmetry axis. Then,
I_CM = MR … (1)

(1) MI about a diameter : Let x- and y-axes be along two perpendicular diameters of the ring as shown in below figure. Let I_x, I_y and I_z be the moments of inertia of the ring about the x, y and z axes, respectively.

Both I_x and I_y represent the moment of inertia of the ring about its diameter and, by symmetry, the MI of the ring about any diameter is the same.
∴ I_x = I_y ….. (2)
Also, I_z being the MI of the ring about its transverse symmetry axis,

(2) MI about a tangent in its plane: Let I be its MI about an axis in plane of the ring, i.e., parallel to a diameter, and tangent to it. Here, h = R and
I_CM = I_x = \(\frac{1}{2}\)MR².
By the theorem of parallel axis,
= \(\frac{1}{2} M R^{2}\) + MR² = \(\frac{3}{2} M R^{2}\) … (7)

Question 79.
State an expression for the MI of a thin uniform disc about a transverse axis through its centre. Hence, derive an expression for the MI of the disc about its tangent perpendicular to the plane. Deduce the expressions for the corresponding radii of gyration.
Answer:
(1) MI about the transverse symmetry axis : Consider a thin uniform disc of radius R and mass M. The axis of rotation through its centre C is perpendicular to its plane. C is also its centre of mass (CM).

Radius of gyration : The radius of gyration of the disc for the given rotation axis is

(2) MI about a tangent perpendicular to its plane : Let I be the MI of the disc about a tangent perpendicular to its plane.

According to the theorem of parallel axis,

Question 80.
Assuming the expression for the moment of inertia of a thin uniform disc about a transverse axis through its centre, obtain an expression for its moment of inertia about any diameter. Hence, write the expression for the corresponding radius of gyration.
Answer:
Consider a thin uniform disc of mass M and radius R in the xy plane, as shown in below figure. Let I_x, I_y and I_z be the moments of inertia of the disc about the x, y and z axes respectively. But, I_x = I_y, since each

represents the moment of inertia (MI) of the disc about its diameter and, by symmetry, the MI of the disc about any diameter is the same.
As I_z is the MI of the disc about the z-axis through its centre and perpendicular to its plane,
I_z = \(\frac{1}{2}\)MR² … (1)

According to the theorem of perpendicular axes,

Question 81.
Given the moment of inertia of a thin uniform disc about its diameter to be \(\frac{1}{4}\)MR², where M and R are respectively the mass and radius of the disc, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Answer:
Consider a thin uniform disc of mass M and radius R in the xy plane. Let Ix, ly and Iz be the moments of inertia of the disc about the x, y and z axes respectively.
Now, I_x = I_y
since each represents the moment of inertia (MI) of the disc about its diameter and, by symmetry, the MI of the disc about any diameter is the same.
∴ I_x = I_y = \(\frac{1}{4}\)MR² (Given)
According to the theorem of perpendicular axes,
I_z = I_x + I_y = 2(\(\frac{1}{4}\)MR²) = \(\frac{1}{2}\)MR²
Let I be the MI of the disc about a tangent normal to the disc and passing through a point on its edge (i.e., a tangent perpendicular to its plane). According to the theorem of parallel axis,
I = I_CM + Mh²
Here, I_CM = I_z = \(\frac{1}{2}\)MR² and h = R.
∴ I = \(\frac{1}{2}\)MR² + MR² = \(\frac{3}{2}\)MR²
which is the required expression.

Question 82.
Assuming the expression for the moment of inertia of a thin uniform disc about its diameter, show that the moment of inertia of the disc about a tangent in its plane is \(\frac{5}{4}\)MR². Write the expression for the corresponding radius of gyration.
Answer:
Let M be the mass and R be the radius of a thin uniform disc. Let I_CM be the moment of inertia (MI) of the disc about a diameter. Then,

Question 83.
State the expressions for the moment of inertia of a solid cylinder of uniform cross section about
(1) an axis through its centre and perpendicular to its length
(2) its own axis of symmetry.
OR
State the expressions for the MI of a solid cylinder about
(1) a transverse symmetry axis
(2) its cylindrical symmetry axis. Also deduce the expressions for the corresponding radii of gyration.
Answer:
Consider a solid cylinder of uniform density, length L, radius R and total mass M.

Notes :

1. For R « L, a solid cylinder can be approximated as a thin rod, and the expression for the MI about its transverse symmetry axis reduces to the corresponding expression for a thin rod, viz., ML²/12.
2. The MI of a solid cylinder about its cylindrical symmetry axis is the same as that of a disc about its transverse symmetry axis and having the same mass and radius.

Question 84.
Assuming the expression for the moment of inertia of a uniform solid cylinder about a transverse symmetry axis, obtain the expression for its moment of inertia about a transverse axis through its one end.
Answer:
Let M be the mass, L the length and R the radius of a uniform solid cylinder. Let I_CM be the moment of inertia (MI) of the cylinder about a transverse symmetry axis. Then,

Question 85.
State an expression for the moment of inertia of a solid sphere about its diameter. Write the expression for the corresponding radius of gyration.
Answer:
Consider a solid sphere of uniform density, radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass.

The MI of the solid sphere about its diameter is
I_CM = \(\frac{2}{5}\)MR²
The corresponding radius of gyration is

Question 86.
A uniform solid sphere of mass 15 kg has radius 0.1 m. What is its moment of inertia about a diameter?
Answer:
Moment of inertia of the sphere about a diameter
= \(\frac{2}{5}\)MR² = \(\frac{2}{5}\) × 15 × (0.1)² = 6 × 10^-2 kg.m²

Question 87.
Assuming the expression for the MI of a uniform solid sphere about its diameter, obtain the expression for its moment of inertia about a tangent.
Answer:
Let M be the mass of a uniform solid sphere of radius R. Let I_CM be its MI about any diameter.

Let I be its MI about a parallel axis, tangent to the sphere. Here, h = R = distance between the two axis.
By the theorem of parallel axis, I = I_CM + Mh²
= \(\frac{2}{5}\)MR² + MR² = \(\frac{7}{5}\)MR²

Question 88.
The moment of inertia of a uniform solid sphere about a diameter is 2 kg m². What is its moment of inertia about a tangent ?
Answer:
Moment of inertia of a solid sphere about its 2
diameter, I_CM = \(\frac{2}{5}\)MR².

Question 89.
The radius of gyration of a uniform solid sphere of radius R is \(\sqrt{\frac{2}{5}}\)R for rotation about its diameter. Show that its radius of gyration for rotation about a tangential axis of rotation is \(\sqrt{\frac{7}{5}}\)R.
Answer:
Let the mass of the uniform solid sphere of radius R be M. Let I_CM and k_d be its MI about any diameter and the corresponding radius of gyration, respectively. Then,

Let I and k_t be its MI about a parallel tangential axis and the corresponding radius of gyration, respectively. Here, h = R = distance between the two axis.
∴ I = \(M k_{\mathrm{t}}^{2}\)
By the theorem of parallel axis,
I = I_CM + Mh²

Question 90.
State the expression for the MI of a thin spherical shell (i.e., a thin-walled hollow sphere) about its diameter. Hence obtain the expression for its MI about a tangent.
Answer:
Consider a uniform, thin-walled hollow sphere radius R and mass M. An axis along its diameter is an axis of spherical symmetry through its centre of mass. The MI of the thin spherical shell about its diameter is
I_CM = \(\frac{2}{3} M R^{2}\)

Let I be its MI about a tangent parallel to the diameter. Here, h = R = distance between the two axes. Then, according to the theorem of parallel axis,

Question 91.
Find the ratio of the radius of gyration of a solid sphere about its diameter to the radius of gyration of a hollow sphere about its tangent, given that both the spheres have the same radius.
Answer:
The radius of gyration of a body about a given axis, k = \(\sqrt{I / M}\), where M and I are respectively the mass of the body and its moment of inertia (MI) about the axis.

For a solid sphere rotating about its diameter,

Question 92.
Calculate the moment of inertia by direct integration of a thin uniform rectangular plate of mass M, length l and breadth b about an axis passing through its centre and parallel to its breadth.
Answer:
Consider a thin uniform rectangular plate of mass M, length l and breadth b. The axis of rotation passes through its centre and is parallel to its breadth. We consider the origin of coordinates to be at the centre of the plate and orient the axes as shown in below figure. Since the plate is thin, we can take the mass as distributed entirely in the xy-plane. Then, the surface mass density is constant and equal to

A rectangular element of the plate, shown shaded, has mass dm, length b and breadth dy.
∴ dm = σdA = σ(b dy)

If the distance of each element from the rotation axis is given by the variable y, the moment of inertia of :
an element about the axis of rotation is
dI_x = y²dm
Since the rod extends from y = -1/2 to y = 1/2, the MI of the thin plate about the axis is

Notes:

(1) The MI of a thin rectangular plate about an axis passing through its centre and parallel to its length (i.e., about the y-axis) is I_y = \(\frac{1}{12}\)Mb². Then, by the theorem of perpendicular axes, the MI of a thin plate about its transverse symmetry axis (i.e., about the z-axis) is I_z = I_x + I_y = \(\frac{1}{12} M\left(l^{2}+b^{2}\right)\)

(2) Suppose, for a rectangular bar of sides l, b and w, we take the origin of coordinates at the centre of mass of the bar and the x, y and z axes parallel to the respective sides. Then, I_x = \(\frac{1}{12}\)M(b² + w²), I_y = \(\frac{1}{12}\)M(w² + l²) and I_z = \(\frac{1}{2} M\left(l^{2}+b^{2}\right)\)

Question 93.
State the MI of a thin rectangular plate-of mass M, length l and breadth b- about an axis passing through its centre and parallel to its length. Hence find its MI about a parallel axis along one edge.
Answer:
Consider a thin rectangular plate of mass M, length l and breadth b. The MI of the plate about an axis passing through its centre and parallel to its edge of length l is

For a parallel axis along its one edge, h = \(\frac{1}{2} b\).
Therefore, by the theorem of parallel axis, the MI about this axis is

Question 94.
State the MI of a thin rectangular plate-of mass M, length l and breadth b about its transverse axis passing through its centre. Hence find its MI about a parallel axis through the midpoint of edge of length b.
Answer:
Consider a thin rectangular plate of mass M, length l and breadth b. The MI of the plate about its transverse axis passing through its centre is
I_CM = M(l² + b²)
For a parallel axis through the midpoint of its breadth, h = \(\frac{1}{2} l\). Therefore, by the theorem of parallel axis, the MI about this axis is

Question 95.
A uniform solid right circular cone of base radius R has mass M. Prove that the moment of inertia of the cone about its central symmetry axis is \(\frac{3}{10} M R^{2}\).
Answer:
Consider a uniform solid right circular cone of mass M, base radius R and height h. The axis of rotation passes through its centre and the vertex, Its constant mass density is

We consider an elemental disc of mass dm, radius r and thickness dz. If the distance of each mass element from the axis is given by the variable z,

Question 96.
Solve the following :

Question 1.
Calculate the moment of inertia of a ring of mass 500 g and radius 0.5 m about an axis of rotation passing through
(i) its diameter
(ii) a tangent perpendicular to its plane.
Solution :
Data : M = 500 g 0.5 kg, R = 0.5 m

(i) The moment of inertia of the ring about its

(ii) The moment of inertia of the ring about a tangent perpendicular to its plane
= 2MR² = 2 × 0.5 × (0.5)² = 0.25 kg.m²

Question 2.
A thin uniform rod 1 m long has mass 1 kg. Find its moment of inertia and radius of gyration for rotation about a transverse axis through a point midway between its centre and one end.
Solution :
Data : M = 1 kg, L = 1 m
Let I_CM and I be the moments of inertia of the rod about a transverse axis through its centre, and a parallel axis midway between its centre and one end.

Question 3.
The moment of inertia of a disc about an axis through its centre and perpendicular to its plane is 10 kg.m². Find its MI about a diameter.
Solution :
Data : I_z = 10 kg.m²
If the disc lies in the xy plane with its centre at the origin then, according to the theorem of perpendicular axes,
I_x + I_y = I_z
Since, I_x = I_y, 2I_x = I_z
∴ Its MI about a diameter,
I_x = \(\frac{I_{z}}{2}\) = \(\frac{10}{2}\) = 5 kg.m²

Question 4.
A solid cylinder of uniform density and radius 2 cm has a mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
Solution :
Data : M = 50 g, R = 2 cm, L = 12 cm

Question 5.
A compound object is formed of a thin rod and a disc attached at the end of the rod. The rod is 0.5 m long and has mass 2 kg. The disc has mass of 1 kg and its radius is 20 cm. Find the moment of inertia of the compound object about an axis passing through the free end of the rod and perpendicular to its length.
Solution :
Data : L = 0.5 m, R = 0.2 m, M_rod = 2 kg, M_disk = 1 kg About a transverse axis through CM,

Question 6.
The radius of gyration of a body about an axis at 6 cm from its centre of mass is 10 cm. Find its radius of gyration about a parallel axis through its centre of mass.
Solution :
Let O be a point at 6 cm from the centre of mass of the body.
Let I = MI about an axis through O,
k = radius of gyration about the axis through O,
I_CM = MI about a parallel axis through the centre of mass of the body,
k_CM = radius of gyration about a parallel axis through the centre of mass,
M = mass of the body,
h = distance between the two axes.
Data : h = 6 cm, k = 10 cm
By the theorem of parallel axis,
I = I_CM + Mh²
Also, I = Mk² and I_CM = \(M k_{\mathrm{CM}}^{2}\)

The radius of gyration about a parallel axis through its centre of mass is 8 cm.

Question 7.
The radius of gyration of a disc about its transverse symmetry axis is 2 cm. Determine its radius of gyration about a diameter.
Solution :
Data : k_CM = 2 cm
Let M and R be the mass and radius of the disc. Let I_CM and k_CM be the MI and radius of gyration of the disc about its transverse symmetry axis. Let I and k be the MI and radius of gyration of the disc about its diameter. Then

Question 8.
Calculate the MI and rotational kinetic energy of a thin uniform rod of mass 10 g and length 60 cm when it rotates about a transverse axis through its centre at 90 rpm.
Solution :
Data : M = 10 g = 10^-2 kg, L = 60 cm = 0.6 m,
f = 90 rpm = 90/60 Hz = 1.5 Hz
The MI of the rod about a transverse axis through its centre is

Angular speed, ω = 2πf = 2 × 3.142 × 1.5 = 9.426 rad/s
Rotational KE = \(\frac{1}{2}\)Iω² = \(\frac{1}{2}\left(3 \times 10^{-4}\right)(9.426)^{2}\)
= 0.01333 J

Question 9.
A thin rod of uniform cross section is made up of two sections made of wood and steel. The wooden section has length 50 cm and mass 0.6 kg. The steel section has length 30 cm and mass 3 kg. Find the moment of inertia of the rod about a transverse axis passing through the junction of the two sections.
Solution:
Data : L₁ =0.5m, M₁ =0.6 kg, L₂ = 0.3m,
The moment of inertia of a thin rod about a transverse axis through its end is \(\frac{M L^{2}}{3}\).

Question 10.
The mass and the radius of the Moon are, respectively, about \(\frac{1}{81}\) time and about \(\frac{1}{3.7}\) time those of the Earth. Given that the rotational period of the Moon is 27.3 days, compare the rotational kinetic energy of the Earth with that of the Moon.
Solution :
Data : M_M = \(\frac{1}{81}\)M_E, R_M = \(\frac{1}{3.7}\)R_E, T_M = 27.3 days, T_E = 1 day

Let I_E and I_M be the moments of inertia of the Earth and the Moon about their respective axes of rotation, and ω_E and ω_M be their respective rotational angular speeds. Assuming the Earth and the Moon to be solid spheres of uniform densities,

Question 11.
A solid sphere of radius R, rotating with an angular velocity ω about its diameter, suddenly stops rotating and 75% of its KE is converted into heat. If c is the specific heat capacity of the material in SI units, show that the temperature of 3R²CO²
the sphere rises by \(\frac{3 R^{2} \omega^{2}}{20 c}\).
Answer:
The MI of a solid sphere about its diameters, I = \(\frac{2}{5}\)MR²
where M is its mass.
The rotational KE of the sphere,

If ∆θ is the rise in temperature,

Question 97.
Define the angular momentum of a particle.
Answer:
Definition : The angular momentum of a particle is defined as the moment of the linear momentum of the particle. If a particle of mass m has linear momentum \(\vec{p}(=m \vec{v})\)), then the angular momentum of this particle with respect to a point O is a vector quantity defined as \(\vec{l}=\vec{r} \times \vec{p}=m(\vec{r} \times \vec{v})\)), where \(\vec{r}\) is the position vector of the particle with respect to O.

It is the angular analogue of linear momentum.

[Note : As the particle moves relative to O in the direction of its momentum \(\vec{p}(=m \vec{v})\), position vector \(\vec{r}\) rotates around O. However, to have angular momentum about O, the particle does not itself have to rotate around O.]

Question 98.
State the dimensions and SI unit of angular momentum.
Answer:

1. Dimensions : [Angular momentum] = [M¹L²T^-1]
2. SI unit: The kilogram.metre²/second (kg.m²/s).

Question 99.
Express the kinetic energy of a rotating body in terms of its angular momentum.
Answer:
The kinetic energy of a body of moment of inertia I and rotating with a constant angular velocity ω is
E = \(\frac{1}{2} I \omega^{2}\)
The angular momentum of the body, L = Iω.
∴E = \(\frac{1}{2}(I \omega) \omega=\frac{1}{2} L \omega\)
This is the required relation.

Question 100.
Why do grinding wheels have large mass and moderate diameter?
Answer:
A grinding wheel, used for abrasive machining operations (e.g., sharpening), is typically in the form of a heavy disc of moderate diameter. A grinding machine needs to have a high frequency of revolution but the machining operations exert braking torques on its wheel.

Angular momentum is directly proportional to mass. Hence, heavier the wheel, the greater is its angular momentum and lesser is the decelerating effect of the braking torques. Also, angular acceleration is inversely proportional to the moment of inertia. Since the wheel is made heavy, its diameter is kept moderate so that a large angular acceleration and high angular velocity can be achieved with a motor of given power.

Question 101.
Solve the following :

Question 1.
The angular momentum of a body changes by 80 kg.m²/s when its angular velocity changes from 20 rad/s to 40 rad/s. Find the change in its kinetic energy of rotation.
Solution :
Data : ω₁ = 20 rad/s, ω₂ = 40 rad/s
If I is the MI of the body, its initial angular momentum is Iω₁, and final angular momentum is Iω₂.
Change in angular momentum
= Iω₂ – Iω₁(ω₂ – ω₁)
∴ 80 = I(40 – 20)
∴ I = 4 kg.m²

Question 2.
A wheel of moment of inertia 1 kg.m² is rotating at a speed of 40 rad/s. Due to the friction on the axis, the wheel comes to rest in 10 minutes. Calculate the angular momentum of the wheel, two minutes before it comes to rest.
Solution :
Data : I = 1 kg.m², ω₁ = 40 rad/s, ω₂ = 0 at
t = 10 minutes = 60 × 10 s = 600 s,
t’ = 8 minutes = 60 × 8 s = 480 s

This is the required angular momentum of the wheel.

Question 3.
A flywheel rotating about an axis through its centre and perpendicular to its plane loses 100 J of energy on slowing down from 60 rpm to 30 rpm. Find its moment of inertia about the given axis and the change in its angular momentum.
Solution :
Data : f₁ = 60 rpm = 60/60 rot/s = 1 rot/s, f₂ = 30 rpm = 30/60 rot/s = \(\frac{1}{2}\) rot/s, ∆E = – 100 J

This gives the MI of the flywheel about the given axis.

(ii) Angular momentum, L = Iω = I(2πf) 2πIf
The change in angular momentum, ∆L
= L₂ – L₁ = 2πI(f₂ – f₁)
= 2 × 3.142 × 6.753\(\left(\frac{1}{2}-1\right)\)
= -3.142 × 6.753= -21.22 kg.m²/s

Question 102.
A torque of 4 N-m acting on a body of mass 1 kg produces an angular acceleration of 2 rad/s². What is the moment of inertia of the body?
Answer:
The moment of inertia of the body.

Question 103.
Two identical rings are to be rotated about different axes of rotation as shown by applying torques so as to produce the same angular acceleration in both. How is it possible ?

Answer:
The MI of ring 1 about a transverse tangent is I₁ = 2MR²
The MI of ring 2 about its diameter is
I₂ = \(\frac{1}{2}\)MR²
Since, torque T = \(\tau=I \alpha\), to produce the same angular acceleration in both,

∴ It will be possible to produce the same angular acceleration in both the rings only if \(\tau_{1}=4 \tau_{2}\).

Question 104.
Two wheels have the same mass. First wheel is in the form of a solid disc of radius R while the second is a disc with inner radius r and outer radius R. Both are rotating with same angular velocity ω₀ about transverse axes through their centres. If the first wheel comes to rest in time t₁ while the second comes to rest in time t₂, are t₁ and t₂ different? Why?
Answer:
The moments of inertia of the two wheels about transverse axes through their centres are

Question 105.
Solve the following :

Question 1.
A torque of magnitude 400 N-m, acting on a body of mass 40 kg, produces an angular acceleration of 20 rad/s². Calculate the moment of inertia and radius of gyration of the body.
Solution :
Data : T = 400 N.m, M = 40 kg, α = 20 rad/s²

Question 2.
A body starts rotating from rest. Due to a couple of 20 N.m, it completes 60 revolutions in one minute. Find the moment of inertia of the body.
Solution :

Question 3.
A wheel of moment of inertia 2 kg-m2 rotates at 50 rpm about its transverse axis. Find the torque that can stop the wheel in one minute.
Solution :
Data : I = 2 kg.m², f₀ = 50 rpm = \(\frac{50}{60}\) = \(\frac{5}{6}\) rev/s, t = 60 s

Question 4.
A circular disc of moment of inertia 10 kg.m² is rotated about its transverse symmetry axis at a constant frequency of 60 rpm by an electric motor of power 31.42 watts. When the motor is switched off, how many rotations does it complete before coming to rest?
Solution :
Data : I = 10 kg.m², P = 31.42 watts,
f = 60 rpm = 60/60 Hz = 1 Hz
In rotational motion,
power = torque × angular velocity

This torque provided by the motor overcomes the torque of the frictional forces and maintains a constant frequency of rotation.

When the motor is switched off, the disc slows down due to the retarding torque of the frictional forces.

Question 5.
A flywheel of mass 4 kg and radius 10 cm, rotating with a uniform angular velocity of 5 rad/s, is subjected to a torque of 0.01 N.m for 10 seconds.
If the torque increases the speed of rotation, find
(i) the final angular velocity of the flywheel
(ii) the change in its angular velocity
(iii) the change in its angular momentum
(iv) the change in its kinetic energy.
Solution :
Data : M = 4 kg, R = 10 cm = 0.1 m, ω₁ = 5 rad/s, \(\tau\) = 0.01 N.m, t = 10 s

(i) The final angular velocity of the flywheel,
ω₂ = ω₁ + αt
= 5 + 0.5 × 10 = 10 rad/s

(ii) The change in its angular velocity
= ω₂ – ω₁ = 5 rad/s

(iii) The change in its angular momentum
= Iω₂ – Iω₁ = I (ω₂ – ω₁)
= 0.02 × 5 = 0.1 kg.m²/s

(iv) The change in its kinetic energy

Question 6.
A torque of 20 N.m sets a stationary circular disc into rotation about a transverse axis through its centre and acts for 2π seconds. If the disc has a mass 10 kg and radius 0.2 m, what is its frequency of rotation after 2π seconds ?
Solution :
Data : \(\tau\) = 20 N.m, t = 2π s, M = 10 kg, R = 0.1 m Let f₁ and f₂ be the initial and final frequencies of rotation of the disc, and ω₁ and ω₂ be its initial and final angular speeds. Since the disc was initially stationary, f₁ = ω₁, = 0 and ω₂ = 2πf₂.
The MI of the disc about the given axis is

Now, ω₂ = ω₁ + αt = 0 + α t
∴ 2πf₂ = αt
∴ f₂ = \(\frac{\alpha t}{2 \pi}\) = \(\frac{100(2 \pi)}{2 \pi}\) = 100 Hz

Question 7.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. If the rope is pulled downwards with a force of 30 N, find
(i) the angular acceleration of the cylinder
(ii) the linear acceleration of the rope.
Solution :
Data : M = 3 kg, R = 0.4 m, F = 30 N
(i) The MI of a hollow cylinder about its cylinder axis, I = MR²

(ii) The linear acceleration of the rope = the tangential acceleration at = αR = 25 × 0.4 = 10 m/s²

Question 106.
State and prove the principle (or law) of conservation of angular momentum.
Answer:
Principle (or law) of conservation of angular momentum : The angular momentum of a body is conserved if the resultant external torque on the body is zero.
Proof : Consider a moving particle of mass m whose position vector with respect to the origin at any instant is \(\vec{r}\).
Then, at this instant, the linear velocity of this particle is \(\vec{v}=\frac{\overrightarrow{d r}}{d t}\), its linear momentum is \(\vec{p}=m \vec{v}\) and its angular momentum about an axis through the origin is \(\vec{l}=\vec{r} \times \vec{p}\).

Suppose its angular momentum \(\vec{l}\) changes with time due to a torque \(\vec{\tau}\) exerted on the particle.

∴ \(\vec{l}\) = constant, i.e., \(\vec{l}\) is conserved. This proves the principle (or law) of conservation of angular momentum.

Alternate Proof : Consider a rigid body rotating with angular acceleration \(\vec{\alpha}\) about the axis of rotation. If I is the moment of inertia of the body about the axis of rotation, \(\vec{\omega}\) the angular velocity of the body at time t and \(\vec{L}\) the corresponding angular momentum of the body, then

∴ \(\vec{L}\) = constant, i.e., \(\vec{L}\) is conserved. This proves the principle (or law) of conservation of angular momentum.

Question 107.
What happens when a ballet dancer stretches her arms while taking turns?
Answer:
When a ballet dancer stretches her arms while pirouetting, her moment of inertia increases, and consequently her angular speed decreases to conserve angular momentum.

Question 108.
If the Earth suddenly shrinks so as to reduce its volume, mass remaining unchanged, what will be the effect on the duration of the day?
Answer:
If the Earth suddenly shrinks, mass remaining constant, the moment of inertia of the Earth will decrease, and consequently the angular velocity of rotation ω about its axis will increase. Since period \(T \propto \frac{1}{\omega}\), the duration of the day T will decrease.

Question 109.
Two discs of moments of inertia I₁ and I₂ about their transverse symmetry axes, respectively rotating with angular velocities to ω₁ and ω₂, are brought into contact with their rotation axes coincident. Find the angular velocity of the composite disc.
Answer:
We assume that the initial angular momenta (\(\vec{L}_{1}\) and \(\vec{L}_{2}\)) of the discs are either in the same direction or in opposite directions. Then,
the total initial angular momentum = \(\vec{L}_{1}+\vec{L}_{2}=I_{1} \overrightarrow{\omega_{1}}+I_{2} \overrightarrow{\omega_{2}}\)

After they are coupled, the total moment of inertia, i.e., the moment of inertia of the composite disc is I = I₁ + I₂ and the common angular velocity is \(\vec{\omega}\). Assuming conservation of angular momentum,

Question 110.
A boy standing at the centre of a turntable with his arms outstretched is set into rotation with angular speed ω rev/min. When the boy folds his arms back, his moment of inertia reduces to \(\frac{2}{5}\)th its initial value. Find the ratio of his final kinetic energy of rotation to his initial kinetic energy.
Answer:
Data : I₂ = \(\frac{2}{5}\)I₁
L = Iω
Assuming the angular momentum \(\vec{L}\) is conserved, in magnitude,

This gives the required ratio.

Question 111.
Name the quantity that is conserved when

1. \(\vec{F}_{\text {external }}\) is zero
2. \(\vec{\tau}_{\text {external }}\) is zero.

Answer:

1. Total linear momentum is conserved when \(\vec{F}_{\text {external }}\) is Zer0
2. Angular momentum is conserved when \(\vec{\tau}_{\text {external }}\) is zero.

Question 112.
What is the rotational analogue of the equation \(\vec{F}_{\text {external }}\) = \(\frac{d \vec{p}}{d t}\)?
Answer:
\(\vec{F}_{\text {external }}\) = \(\frac{d \vec{L}}{d t}\)

Question 113.
Fly wheels used in automobiles and steam engines producing rotational motion have discs with a large moment of inertia. Explain why?
Answer:
A flywheel is used as

(i) a mechanical energy storage, the energy being stored in the form of rotational kinetic energy

(ii) a direction and speed stabilizer. A flywheel rotor is typically in the form
of a disc. Rotational kinetic energy, \(E_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}\), where I is the moment of inertia and ω is the angular speed. That is, E_rot ∝ I. Therefore, higher the moment of inertia, the higher is the rotational kinetic energy that can be stored or recovered.

Also, angular momentum, \(\vec{L}=I \vec{\omega}\), i.e., \(|\vec{L}| \propto I\). A torque aligned with the symmetry axis of a flywheel can change its angular velocity and thereby its angular momentum. A flywheel with a large angular momentum will require a greater torque to change its angular velocity. Thus, a flywheel can be used to stabilize direction and magnitude of its angular velocity by undesired torques.

Question 114.
Solve the following :

Question 1.
A uniform horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of 180 rpm. A blob of wax of mass 1.9 g falls on it and sticks to it at 25 cm from the axis. If the frequency of rotation is reduced by 60 rpm, calculate the moment of inertia of the disc.
Solution :
Data : f₁ = 180 rpm = 180/60 rot/s = 3 rot/s, f₂ = (180 – 60) rpm = 120/60 rot/s = 2 rot/s, m = 1.9 g = 1.9 × 10^-3 kg, r = 25 cm = 0.25 m
Let I₁ be the MI of the disc. Let I₂ be the MI of the disc and the blob.

Question 2.
A horizontal disc is rotating about a transverse axis through its centre at 100 rpm. A 20 gram blob of wax falls on the disc and sticks to it at 5 cm from its axis. The moment of inertia of the disc about its axis passing through its centre is 2 × 10^-4 kg.m². Calculate the new frequency of rotation of the disc.
Solution :
Data : f₁ = 100 rpm, m = 20 g = 20 × 10^-3 kg, r = 5 cm = 5 × 10^-2 m, I₁ = I_disc = 2 × 10^-4 kg.m²
The MI of the disc and blob of wax is
I₂ = I₁ + mr²

This is the new frequency of rotation.

Question 3.
A ballet dancer spins about a vertical axis at 2.5 π rad/s with his arms outstretched. With the arms folded, the MI about the same axis of rotation changes by 25%. Calculate the new speed of rotation in rpm.
Solution:
Let I₁, ω₁, and f₁, be the moment of inertia, angular velocity and frequency of rotation of the ballet dancer with arms outstretched, and I₂, ω₂ and f₂ be the corresponding quantities with arms folded.
Data : ω₁ = 2.5 π rad /s
Since moment of inertia with arms folded is less than that with arms outstretched,

Question 4.
Two wheels, each of moment of inertia 4 kg.m², rotate side by side at the rate of 120 rpm and 240 rpm in opposite directions. If both the wheels are coupled by a weightless shaft so that they now rotate with a common angular speed, find this new rate of rotation.
Solution :
Data : I = 4 kg.m², f₁ = 120 rpm, f₂ 240 rpm
Initially, the angular velocities of the two wheels \(\overrightarrow{\omega_{1}}\), and \(\overrightarrow{\omega_{2}}\)) and, therefore, their angular momenta (\(\vec{L}_{1}\) and \(\vec{L}_{2}\)) are in opposite directions.

The magnitude of the total initial angular momentum
= – L₁ + L₂ = -Iω₁ + Iω₂ (∵ I₁ = I₂ = I)
= 2πl(f₂ – f₁) … (1)

After coupling onto the same shaft, the total moment of inertia is 21. Let ω = 2πf be the common angular speed.

The magnitude of the total final angular momentum = 2I.ω = 4πl.f … (2)

From Eqs. (1) and (2), by the principle of conservation of angular momentum,
4πf = 2πl(f₂ – f₁)
∴ f = \(\frac{f_{2}-f_{1}}{2}\) = \(\frac{240-120}{2}\) = 60 rpm
This gives their new rate of rotation.

Question 5.
A homogeneous (uniform) rod XY of length L and mass M is pivoted at the centre C such that it can rotate freely in a vertical plane. Initially, the rod is horizontal. A blob of wax of the same mass M as that of the rod falls vertically with speed V and sticks to the rod midway between points C and Y. As a result, the rod rotates with angular speed ω. What will be the angular speed in terms of V and L?
Solution :
The initial angular momentum of the rod is zero.
The initial angular momentum of the falling blob of wax about the point C is (in magnitude)
= mass × speed × perpendicular distance between its direction of motion and point C
= MV.\(\frac{L}{4}\)
The total initial angular momentum of the rod and blob of wax = \(\frac{M V L}{4}\) … (1)

After the blob of wax sticks to the rod, and the system rotates with an angular speed ω about the horizontal axis through point C perpendicular to the plane of the figure, the total final angular momentum of the system about this axis

This gives the required angular speed.

Question 6.
A satellite moves around the Earth in an elliptical orbit such that at perigee (closest approach) it is two Earth radii above the Earth’s surface. At apogee (farthest position), it travels with one-fourth the speed it has at perigee. In terms of the Earth’s radius R, what is the maximum distance of the satellite from the Earth’s surface ?
Solution:
Let r_p and r_a be the distances of the satellite from the centre of the Earth at perigee and apogee, respectively. Let v_p and v_a be its linear (tangential) velocities at perigee and apogee.
Data : r_p = 2R + R = 3R, v_a = \(\frac{1}{4}\)v_p

Let L_p and L_a be the angular momenta of the satellite about the Earth’s centre. Because the gravitational force (\(\vec{F}\)) on the satellite due to the Earth is always radially towards the centre of the Earth, its direction is opposite to that of the position vector (\(\vec{r}\)) of the satellite relative to the centre of the Earth, so that the torque \(\vec{\tau}=\vec{r} \times \vec{F}=0\). Hence, the angular momentum of the satellite about the Earth’s centre is constant in time.

At apogee, the distance of the satellite from the Earth’s surface is 12R – R = 11R.

Question 7.
A torque of 100 N.m is applied to a body capable of rotating about a given axis. If the body starts from rest and acquires kinetic energy of 10000 J in 10 seconds, find
(i) its moment of inertia about the given axis
(ii) its angular momentum at the end of 10 seconds.
Solution :
Data : \(\tau\) = 100 N.m, ω_i = 0, E_i = 0, E_f = 10⁴J, t = 10 s

Since the body starts from rest, its initial angular momentum, L_i = 0.
The final angular momentum,
L_f = τ∆t = (100)(10) = 10³ kg.m²/s
The final rotational kinetic energy, E_f = \(\frac{1}{2} L_{\mathrm{f}} \omega_{\mathrm{f}}\)

Question 8.
Two identical metal beads, each of mass M but negligible width, can slide along a thin smooth uniform horizontal rod of mass M and length L. The rod is capable of rotating about a vertical axis passing through its centre. Initially, the beads are almost touching the axis of rotation and the rod is rotating at speed of 14 rad/s. Find the angular speed of the system when the beads have moved up to the ends of the rod. (Assume that no external torque acts on the system.)
Solution :
Data : ω₁ = 14 rad/s
The MI of the rod about a transverse axis through its CM,
I_rod = \(\frac{M L^{2}}{12}\)
Since the beads are almost particle-like, and initially touching the rotation axis, their MI about the vertical axis is taken to be zero.
When the beads move upto the ends of the rod, r = L/2, their MI about the vertical axis is

Question 115.
Discuss how pure rolling (i.e., rolling without slipping) on a plane surface is a combined translational and rotational motion.
Answer:
Rolling motion (without slipping) is an important case of combined translation and rotation. Consider a circularly symmetric rigid body, like a wheel or a disc, rolling on a plane surface with friction along a straight path.

The centre of mass of the wheel is at its geometric centre O. For purely translational motion (the wheel sliding smoothly along the surface without rotating at all), every point on the wheel has the same linear velocity \(\vec{v}_{\mathrm{CM}}\) = \(\vec{v}_{\mathrm{O}}\) as the centre O. For purely rotational motion (as if the horizontal rotation axis through O were stationary), every point on the wheel rotates about the axis with angular velocity \(\vec{\omega}\); in this case, every point on the rim has the same linear speed ωR.

We view the combined motion in the inertial frame of reference in which the surface is at rest. In this frame, since there is no slipping, the point of contact of the wheel with the surface is instantaneously stationary, v_A = 0, so that the wheel is turning about an instantaneous axis through the point of contact A. The instantaneous linear speed of point C (at the top) is V_C = ω(2R) – faster than any other point of the wheel.

Question 116.
Deduce an expression for the kinetic energy of a body rolling on a plane surface without slipping.
OR
Obtain an expression for the total kinetic energy of a rolling body in the form \(\frac{1}{2} M v^{2}\left[1+\frac{k^{2}}{R^{2}}\right]\)
OR
Derive an expression for the kinetic energy when a rigid body is rolling on a horizontal surface without slipping. Hence, find the kinetic energy of a solid sphere.
Answer:
Consider a symmetric rigid body, like a sphere or a wheel or a disc, rolling on a plane surface with friction along a straight path. Its centre of mass (CM) moves in a straight line and, if the frictional force on the body is large enough, the body rolls without slipping. Thus, the rolling motion of the body can be treated as translation of the CM and rotation about an axis through the CM. Hence, the kinetic energy of a rolling body is
E = E_tran + E_rot ….. (1)
where E_tran and E_rot are the kinetic energies associated with translation of the CM and rotation about an axis through the CM, respectively.

Let M and R be the mass and radius of the body. Let ω, k and I be the angular speed, radius of gyration and moment of inertia for rotation about an axis through its centre, and v be the translational speed of the centre of mass.

Equation (4) or (5) or (6) gives the required expression.

Question 117.
A uniform solid sphere of mass 10 kg rolls on a horizontal surface. If its linear speed is 2 m/s, what is its total kinetic energy?
Answer:
Total kinetic energy of the sphere
= \(\frac{7}{10}\)Mv² = \(\frac{7}{10}\) × 10 × (2)² = 28 J

Question 118.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/s, what is its total kinetic energy?
Answer:
Total kinetic energy of the disc
= \(\frac{3}{4}\)Mv² = \(\frac{3}{4}\) × 4 × (3)² = 27 J

Question 119.
Assuming the expression for the kinetic energy of a body rolling on a plane surface without slipping, deduce the expression for the total kinetic energy of rolling motion for
(i) a ring
(ii) a disk
(iii) a hollow sphere. Also, find the ratio of rotational kinetic energy to total kinetic energy for each body.
Answer:
For a body of mass M and radius of gyration k, rolling on a plane surface without slipping with speed v, its total KE and rotational KE are respectively

[Note : The moment of inertia of all the round bodies above can be expressed as I = βMR², where β is a pure number less than or equal to 1. β is equal to 1 for a ring or a thin-walled hollow cylinder, \(\frac{1}{2}\) for a disc or solid cylinder, \(\frac{2}{3}\) for a hollow sphere and \(\frac{2}{5}\) for a solid sphere.
All uniform rings or hollow cylinders of the same mass and moving with the same speed have the same total kinetic energy, even if their radii are different. All discs or solid cylinders of the same mass and moving with the same speed have the same total kinetic energy; all solid spheres of the same mass and moving with the same speed have the same total kinetic energy. Also, for the same mass and speed, bodies with small c have less total kinetic energy.

Question 120.
State the expression for the speed of a circularly symmetric body rolling without slipping down an inclined plane. Hence deduce the expressions for the speed of
(i) a ring
(ii) a solid cylinder
(iii) a hollow sphere
(iv) a solid sphere, having the same radii.
Answer:
Consider a circularly symmetric body, of mass M and radius of gyration k, starting from rest on an inclined plane and rolling down without slipping. Its speed after rolling down through a height h is

[Note : If the inclined plane is ‘smooth’, i.e., there is no friction, the bodies will slide along the plane without any rotation. They will then have only translational kinetic energy, undergo equal acceleration and all three would arrive at the bottom at the same time with the same speed.]

Question 121.
State with reason if the statement is true or false : A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
Answer:
The statement is true.
Explanation : Rolling on a surface (horizontal or inclined) without slipping may be viewed as pure rotation about an horizontal axis through the point of contact, when viewed in the inertial frame of reference in which the surface is at rest. The point of contact of the wheel with the surface will be instantaneously at rest, resulting in a rolling motion, provided the wheel is able to ‘grip’ the surface, i.e., friction is necessary. With little or no friction, the wheel will slip at the point of contact. On an inclined plane, this will result in pure translation along the plane. On a horizontal surface, the wheel will simply rotate about its axis through the centre without translation.

Question 122.
A ring and a disc roll down an inclined plane through the same height. Compare their speeds at the bottom of the plane.
Answer:

Question 123.
State the expression for the acceleration of a circularly symmetric rigid body rolling without slipping down an inclined plane. Hence, deduce the acceleration of
(i) a ring
(ii) a solid cylinder
(iii) a hollow cylinder
(iv) a solid sphere, rolling without slipping down an inclined plane.
Answer:
A circularly symmetric rigid body, of radius R and radius of gyration k, on rolling down an inclined plane of inclination θ has an acceleration

Question 124.
A spherical shell rolls down a plane inclined at 30° to the horizontal. What is its acceleration ?
Answer:
The acceleration of the spherical shell,
a = \(\frac{3}{5} g \sin \theta\) = 0.6g sin 30° = 0.6g × \(\frac{1}{2}\) = 0.3g m

Question 125.
A spherical shell and a uniform solid sphere roll down the same inclined plane. Compare their accelerations.
Answer:
The ratio of the accelerations, in the usual notation,

Question 126.
A solid sphere, starting from rest, rolls down two different inclined planes from the same height but with different angles of inclination θ₁ > θ₂. On which plane will the sphere take longer time to roll down?
Answer:
Let L₁ and L₂ be the distances rolled down by the sphere along the corresponding inclines from the same height h.
∴ L₁ sin θ₁ = L₂ sin θ₂ = h

The sphere will take longer time to roll down from the same height on the plane with smaller inclination.

Question 127.
Two circular discs A and B, having the same mass, have four identical small circular discs placed on them, as shown in the diagram. They are simultaneously released from rest at the top of an inclined plane. If the discs roll down without slipping, which disc will reach the bottom first?

Answer:
The disc A has the smaller discs closer to the centre than disc B. Hence, the moment of inertia of disc A (I_A) is less than that of disc B (I_B).

[Suppose the larger discs have radius R, the smaller discs have mass m and radius r, and the centre of each smaller disc on disc A is at a distance x from the centre. Then, x = \(\sqrt{2} r\)r and, it can be shown that, I_B – I_A = 4m[R² – (x – r)²] > 0.]

Each composite disc is equivalent to a disc of the same radius R and mass M’ = M + 4m, where m is the mass of each smaller disc, but of different thicknesses.

Suppose, starting from rest, the composite discs roll down the same distance L along a plane inclined at an angle θ, their respective accelerations will be

i.e., the disc A will reach the bottom first.

Question 128.
Solve the following :

Question 1.
A lawn roller of mass 80 kg, radius 0.3 m and moment of inertia 3.6 kg.m², is drawn along a level surface at a constant speed of 1.8 m/s. Find
(i) the translational kinetic energy
(ii) the rotational kinetic energy
(iii) the total kinetic energy of the roller.
Answer:
Data : M = 80 kg, R = 0.3 m, I = 3.6 kg.m², v = 1.8 m/s
(i) The translational kinetic energy of the centre of mass of the roller,

Question 2.
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
Solution :
Data : M = 1 kg, v = 2 m/s
The total kinetic energy of a rolling body,

Question 3.
A ring and a disc having the same mass roll on a horizontal surface without slipping with the same linear velocity. If the total KE of the ring is 8 J, what is the total KE of the disc?
Solution :
Data : M_ring = M_disc = M, v_ring = v_disc = v, E_ring = 8J
The total kinetic energies of rolling without slipping on a horizontal surface,
E_ring = Mv² and E_disc = \(\frac{3}{4} M v^{2}\)
since they have the same mass and linear velocity.
∴ E_disc = \(\frac{3}{4}\)E_ring = \(\frac{3}{4}\) × 8 = 6J

Question 4.
A solid cylinder, of mass 2 kg and radius 0.1 m, rolls down an inclined plane of height 3 m. Calculate its rotational energy when it reaches the foot of the plane.
Solution :
Data : M = 2 kg, R = 0.1 m, h = 3 m, g = 10 m/s²

Question 5.
A solid sphere rolls up a plane inclined at 45° to the horizontal. If the speed of its centre of mass at the bottom of the plane is 5 m/s, find how far the sphere travels up the plane.
Solution :
Data : v = 5 m/s, θ = 45°, g = 9.8 m/s²
The total energy of the sphere at the bottom of the plane is
E = \(\frac{7}{10} M v^{2}\)
where M is the mass of the sphere.
In rolling up the incline through a vertical height h, it travels a distance L along the plane. Then,

The sphere travels 2.526 m up the plane.

Question 129.
Choose the correct option:

Question 1.
The bulging of the Earth at the equator and flattening at the poles is due to
(A) centripetal force
(B) centrifugal force
(C) gravitational force
(D) electrostatic force.
Answer:
(B) centrifugal force

Question 2.
A body of mass 0.4 kg is revolved in a horizontal circle of radius 5 m. If it performs 120 rpm, the centripetal force acting on it is
(A) 4π² N
(B) 8π² N
(C) 16π² N
(D) 32π² N.
Answer:
(D) 32π² N.

Question 3.
Two particles with their masses in the ratio 2 : 3 perform uniform circular motion with orbital radii in the ratio 3 : 2. If the centripetal force acting on them is the same, the ratio of their speeds is
(A) 4 : 9
(B) 1 : 1
(C) 3 : 2
(D) 9 : 4.
Answer:
(C) 3 : 2

Question 4.
When a motorcyclist takes a circular turn on a level race track, the centripetal force is
(A) the resultant of the normal reaction and frictional force
(B) the horizontal component of the normal reaction
(C) the frictional force between the tyres and road
(D) the vertical component of the normal reaction.
Answer:
(C) the frictional force between the tyres and road

Question 5.
The maximum speed with which a car can be driven safely along a curved road of radius 17.32 m and banked at 30° with the horizontal is [g = 10 m/s²]
(A) 5 m/s
(B) 10 m/s
(C) 15 m/s
(D) 20 m/s.
Answer:
(B) 10 m/s

Question 6.
A track for a certain motor sport event is in the form of a circle and banked at an angle 6. For a car driven in a circle of radius r along the track at the optimum speed, the periodic time is

Answer:
(C) \(2 \pi \sqrt{\frac{r}{g \tan \theta}}\)

Question 7.
The period of a conical pendulum in terms of its length (l), semivertical angle (θ) and acceleration due to gravity (g), is

Answer:
(C) \(4 \pi \sqrt{\frac{l \cos \theta}{4 g}}\)

Question 8.
A conical pendulum of string length L and bob of mass m performs UCM along a circular path of radius r. The tension in the string is

Answer:
(A) \(\frac{m g L}{\sqrt{L^{2}-r^{2}}}\)

Question 9.
The centripetal acceleration of the bob of a conical pendulum is

Answer:
(D) \(\frac{r g}{L \cos \theta}\)

Question 10.
A small object tied at the end of a string is to be whirled in a vertical circle of radius r. If its speed at the lowest point is \(2 \sqrt{g r}\), then
(A) the string will be slack at the lowest point
(B) it will not reach the midway point
(C) its speed at the highest point will be \(\sqrt{g r}\)
(D) it will just reach the highest point with zero speed.
Answer:
(D) it will just reach the highest point with zero speed.

Question 11.
A small bob of mass m is tied to a string and revolved in a vertical circle of radius r. If its speed at the highest point is \(\sqrt{3 r g}\), the tension in the string at the lowest point is
(A) 5 mg
(B) 6 mg
(C) 7 mg
(D) 8 mg.
Answer:
(D) 8 mg.

Question 12.
A small object, tied at the end of a string of length r, is launched into a vertical circle with a speed \(2 \sqrt{g r}\) at the lowest point. Its speed when the string is horizontal is
(A) > \(3 \sqrt{g r}\)
(B) = \(3 \sqrt{g r}\)
(C) = \(2 \sqrt{g r}\)
(D) 0.
Answer:
(C) = \(2 \sqrt{g r}\)

Question 13.
Two bodies with moments of inertia I₁ and I₂ (I₁ > I₂) rotate with the same angular momentum. If E₁ and E₂ are their rotational kinetic energies, then
(A) E₂ > E₁
(B) E₂ = E₁
(C) E₂ < E₁
(D) E₂ ≤ E₁
Answer:
(A) E₂ > E₁

Question 14.
The radius of gyration k for a rigid body about a given rotation axis is given by

Answer:
(B) \(k^{2}=\frac{1}{M} \int r^{2} d m\)

Question 15.
Three point masses m, 2m and 3m are located at the three vertices of an equilateral triangle of side l. The moment of inertia of the system of particles about an axis perpendicular to their plane and equidistant from the vertices is
(A) 2ml²
(B) 3ml²
(C) \(2 \sqrt{3}\) ml²
(D) 6ml²
Answer:
(A) 2ml²

Question 16.
The moment of inertia of a thin uniform rod of mass M and length L, about an axis passing through a point midway between the centre and one end, and perpendicular to its length, is
(A) \(\frac{48}{7}\)ML²
(B) \(\frac{7}{48}\)ML²
(C) \(\frac{1}{48}\)ML²
(D) \(\frac{1}{16}\)ML²
Answer:
(B) \(\frac{7}{48}\)ML²

Question 17.
A thin uniform rod of mass M and length L has a small block of mass M attached at one end. The moment of inertia of the system about an axis through its CM and perpendicular to the length of the rod is
(A) \(\frac{13}{12}\) ML²
(B) \(\frac{1}{3}\) ML²
(C) \(\frac{5}{24}\) ML²
(D) \(\frac{7}{48}\) ML²
Answer:
(C) \(\frac{5}{24}\) ML²

Question 18.
A thin wire of length L and uniform linear mass density λ is bent into a circular ring. The MI of the ring about a tangential axis in its plane is

Answer:
(C) \(\frac{3 \lambda L^{3}}{8 \pi^{2}}\)

Question 19.
When a planet in its orbit changes its distance from the Sun, which of the following remains constant ?
(A) The moment of inertia of the planet about the Sun
(B) The gravitational force exerted by the Sun on the planet
(C) The planet’s speed
(D) The planet’s angular momentum about the Sun
Answer:
(D) The planet’s angular momentum about the Sun

Question 20.
If L is the angular momentum and I is the moment of inertia of a rotating body, then \(\frac{L^{2}}{2 I}\) represents its
(A) rotational PE
(B) total energy
(C) rotational KE
(D) translational KE.
Answer:
(C) rotational KE

Question 21.
A thin uniform rod of mass 3 kg and length 2 m rotates about an axis through its CM and perpendicular to its length. An external torque changes its frequency by 15 Hz in 10 s. The magnitude of the torque is
(A) 3.14 N.m
(B) 6.28 N.m
(C) 9.42 N.m
(D) 12.56 N.m.
Answer:
(C) 9.42 N.m

Question 22.
The flywheel of a motor has mass 300 kg and radius of gyration 1.5 m. The motor develops a constant torque of 2000 N.m and the flywheel starts from rest. The work done by the motor during the first 4 revolutions is
(A) 2 kJ
(B) 8 kJ
(C) 8n kJ
(D) 16π kJ.
Answer:
(D) 16π kJ.

Question 23.
Two uniform solid spheres, of the same mass but radii in the ratio R₁ : R₂ = 1 : 2, roll without slipping on a plane surface with the same total kinetic energy. The ratio ω₁ : ω₂ of their angular speed is
(A) 2 : 1
(B) \(\sqrt{2}\) : 1
(C) 1 : 1
(D) 1 : 2.
Answer:
(A) 2 : 1

Question 24.
A circularly symmetric body of radius R and radius of gyration k rolls without slipping along a flat surface. Then, the fraction of its total energy associated with rotation is [c = k²/R²]
(A) c
(B) \(\frac{c}{1+c}\)
(C) \(\frac{1}{c}\)
(D) \(\frac{1}{1+c}\)
Answer:
(B) \(\frac{c}{1+c}\)

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 8 Memory Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 8 Memory

1A. Complete the following statements.

Question 1.
__________ is the retention of information over time for the purpose of future action.
(A) Learning
(B) Memory
(C) Attention
Answer:
(B) Memory

Question 2.
__________ plays an important role in storage of memory.
(A) Hippocampus
(B) Amygdala
(C) Nervous system
Answer:
(A) Hippocampus

Question 3.
The term __________ memory was coined by Miller, Galanter, and Pribram around 1960.
(A) sensory
(B) working
(C) long-term
Answer:
(B) working

Question 4.
Visuo-spatial sketch pad (VSSP) is a/an __________ system.
(A) passive
(B) active
(C) non-functional
Answer:
(A) passive

Question 5.
Autobiographical memory is a type of __________ memory.
(A) implicit
(B) procedural
(C) declarative
Answer:
(C) declarative

Question 6.
In __________ recall, the material is recalled in the exact order in which it was presented.
(A) serial
(B) free
(C) definite
Answer:
(A) serial

Question 7.
__________ is one of the major ways of measuring memory.
(A) Rote learning
(B) Perception
(C) Relearning
Answer:
(C) Relearning

Question 8.
__________ is the evidence for the organisation of long-term memory.
(A) Serial recall
(B) Tip of the tongue phenomenon
(C) Recognition
Answer:
(B) Tip of the tongue phenomenon

Question 9.
The pioneer of experiments on forgetting was __________
(A) Murdock
(B) Hermann Ebbinghaus
(C) Baddeley
Answer:
(B) Hermann Ebbinghaus

Question 10.
__________ interference means backward interference.
(A) Retroactive
(B) Proactive
(C) Passive
Answer:
(A) Retroactive

Question 11.
__________ is a Greek word meaning ‘of memory or related to memory.’
(A) Mnemonic
(B) Syllable
(C) LTM
Answer:
(A) Mnemonic

Question 12.
The final stage in POWER method is __________
(A) evaluate
(B) rethink
(C) relearn
Answer:
(B) rethink

1B. Match the following pairs.

Question 1.

A	B
i. LTM	a. Conscious
ii. Explicit memory	b. Less than one second
iii. Sensory memory	c. Life-time memory
iv. Procedural memory	d. Autobiographical events
	e. Unconscious

Answer:

A	B
i. LTM	c. Life-time memory
ii. Explicit memory	a. Conscious
iii. Sensory memory	b. Less than one second
iv. Procedural memory	e. Unconscious

1C. State whether the following statements are true or false. If false, correct them. If true, explain why.

Question 1.
There are four basic processes of memory.
Answer:
False
Reason: There are three basic processes of memory, viz. encoding/acquisition, storage, and retrieval.

Question 2.
Short-term memory is known by many other terms.
Answer:
True
Explanation: Short-term or working memory was formerly known as ‘short term store’. It is also known as primary memory, immediate memory, operant memory, and provisional memory.

Question 3.
Baddeley called LTM the working bench of memory.
Answer:
False
Reason: Baddeley called STM the working bench of memory because STM is the most important stage of memory which is used most of the time for problem-solving.

Question 4.
Very often forgetting is due to unconscious processes like repression.
Answer:
True
Explanation: We subconsciously push unwanted thoughts and memories into our unconsciousness. It is one of the causes of forgetting.

Question 5.
In recognition, a person has to retrieve information from LTM with no cues.
Answer:
False
Reason: In recognition, a person has to point out or recognize previously learned material that is presented to him in a different context.

Question 6.
There are five levels of motivated forgetting.
Answer:
False
Reason: There are two levels of motivated forgetting, viz. Repression and Thought suppression.

Question 7.
The Method of Loci provides information about how context can affect memory.
Answer:
False
Reason: ‘The encoding specificity of memory’ provides information about how context can affect memory.

Question 8.
There are many techniques for improving memory.
Answer:
True
Explanation: Some of the techniques of improving memory are keyword method, encoding specificity, method of loci, mnemonic devices, practice, and rehearsal, minimizing interference, and POWER method.

1D. Identify the odd item from the following.

Question 1.
Episodic memory, Semantic memory, Autobiographical memory, Implicit memory
Answer:
Implicit memory

2A. Explain the following concepts

Question 1.
Memory
Answer:
According to Tulving, ‘Memory is the means by which we draw on our past experiences in order to use that information in the present. Memory is the term given to the structure and processes involved in the storage and subsequent retrieval of information.

Question 2.
Central executive
Answer:
The central executive is a supervisor responsible for the coordination of the subsystems and the selection of reasoning and storage strategies in the working memory model given by Baddeley.

Question 3.
Episodic buffer
Answer:
The episodic buffer holds information that is not covered by all other slave systems in the working memory model given by Baddeley. It is a link between working memory and long-term memory.

Question 4.
Autobiographical memory
Answer:
Autobiographical memory refers to episodes recollected from an individual’s own life. It is a type of declarative memory.

Question 5.
Flashbulb memory
Answer:
Flashbulb memory is a highly detailed and exceptionally clear ‘snapshot’ of mostly a traumatic moment. It is a type of autobiographical memory. Flashbulb memories illustrate that exceptional memories are easily retrieved.

Question 6.
Relearning
Answer:
Relearning measures retention by measuring how much faster one learns a previously learned material after an interval of time, i.e. the same material is learned by the same subject based on the same learning criterion at two different occasions separated by time interval.

Question 7.
Forgetting
Answer:
Forgetting is the inability to remember the things which we want to remember at that moment. In other words, it is the failure to retrieve the material from our long-term memory which we have already stored.

2B. Compare and contrast.

Question 1.
Primacy effect and Recency effect
Answer:

• The primacy effect occurs when the subject is able to recall items that are presented at the starting point of the list while the recency effect occurs when the subject is able to recall the items which are presented at the end. Free recall is effective in studying both these effects.
• Both primary and recency effect was witnessed in Murdock’s experiment where subjects could prominently recall the first few and last few words from the list.
• The primacy effect is the tendency to remember the first piece of information that we encounter in a better manner than the information presented later on. Conversely, the recency effect is the tendency to remember the most recent information in a better way.

Question 2.
Retroactive interference and Proactive interference
Answer:

• Retroactive interference is the partial or complete forgetfulness of the previously learned material due to new memories that get mixed up with the older ones. On the other hand, proactive interference is the partial or complete forgetfulness of newly learned material due to the old material.
• e.g. You studied Psychology yesterday and you studied Sociology today. If you forget Psychology due to the study of Sociology, it is due to retroactive interference while if you forget Sociology due to the study of Psychology, it is due to proactive interference.

3. Answer the following questions in around 35-40 words each.

Question 1.
State the types of human memory.
Answer:
The following flow chart explains types of human memory:

Question 2.
Explain the stages of memory.
Answer:

• Environmental stimulus is received with the help of sense organs (sensory information store). This is where the memory is stored.
• When we pay attention to the sensations, they are transferred to STM.
• If information is rehearsed or appears frequently, then it is transferred to the LTM.
  
• After encountering any problem, we bring the information from LTM to STM so that it’s available for solving the problem.

Question 3.
What do you mean by magical number 7?
Answer:

• The magical number 7+/-2 provides evidence for a limited capacity of the STM.
• Most adults can store between five and nine items in the STM.
• This idea was put forward by George Miller in 1956 and hence called 7 as a magical number.

Question 4.
What is the Phonological Loop (PL)?
Answer:

• The Phonological loop is responsible for verbal information.
• It has two subsystems as follows:
  • The phonological/acoustic store is a passive component of the phonological loop. It holds on verbal information. If not rehearsed, this information is forgotten.
  • The articulatory loop involves rehearsing and refreshing the information, just like our inner voice.

Question 5.
Explain Murdock’s experiment.
Answer:

• Murdock performed experiments to check the recall.
• He asked his subjects to learn a list of words. Later, their recall was tested by a free recall method.
• Murdock found that the subjects could recall the first few (primacy effect) and the last few (recency effect) words prominently. But they got confused with the words in the middle part (serial position effect).

4. Short Notes.

Question 1.
visuospatial Sketch Pad (VSSP)
Answer:

• VSSP handles visual and spatial information. It is responsible for storing speech-based information.
• It has two components, viz. Phonological memory store and Articulatory Subvocal Rehearsal.
• Phonological memory stores can hold traces of acoustic or speech-based information.
• Articulatory Subvocal Rehearsal maintains material in short-term store. Prevention of articulatory rehearsal leads to rapid forgetting.

Question 2.
Recall
Answer:

• The recall is the retrieval of information from LTM with few or no cues. Recall can be in the written form or it can be oral.
• The recall involves remembering a fact, event, or object that is not currently physically present and requires the direct uncovering of information from memory.
• The recall is of two types, viz. free recall and serial recall.
• Free recall is a recollection of the items in the list without their serial order, e.g. we may listen to a lecture and later recall few important points irrespective of the order in which they were presented.
• In serial recall, the material is recalled in the exact order in which it was presented, e.g. when you solve a mathematical problem, you are doing steps one after the other; so, it is serial recall.
• The recall is greatly affected by emotions and motivation at the time of learning and retrieval.
• Also, memory for the free recall is always better than if the subjects are asked to recall in a serial order.

Question 3.
Hermann Ebbinghaus’s experiment
Answer:

• The pioneer of experiments on forgetting was Hermann Ebbinghaus.
• He created several lists of nonsense syllables and learned them. A nonsense syllable is a set of three alphabets where two on both the sides are consonants and the middle one is a vowel, e.g. NOM, GEX.
• He checked his own recall at various periods of time.
• He found out that he forgot 40% of whatever he had learned in the first 20 minutes.
• After one hour, he forgot 60% while after nine hours he forgot a total of 70% of what he had learned.
• After one day, he could recall only around 30% of the material he learned. After that, his recall was steady for a long period of time.
• This experiment proved that we forget most of the things we learn in a short span.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 7 Nervous System Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 7 Nervous System

1A. Complete the following statements with appropriate options.

Question 1.
__________ of the neuron absorbs the food and keeps the cell alive.
(A) Nucleus
(B) Axon
(C) Cell body
Answer:
(A) Nucleus

Question 2.
__________ plays a role mainly in cognition, reward, learning and memory.
(A) Acetylcholine
(B) Dopamine
(C) Serotonin
Answer:
(C) Serotonin

Question 3.
The brain plays an important role in __________ mental processes like thinking, reasoning, and emotions.
(A) higher-order
(B) lower order
(C) neutral
Answer:
(A) higher-order

Question 4.
Cerebellum consists of __________ parts.
(A) two
(B) three
(C) four
Answer:
(A) two

Question 5.
__________ is a vital centre of the brain.
(A) Medulla oblongata
(B) Pons
(C) Forebrain
Answer:
(A) Medulla oblongata

Question 6.
__________ is a bridge between forebrain and hindbrain.
(A) Pons
(B) Midbrain
(C) Cerebrum
Answer:
(B) Midbrain

Question 7.
Cerebrum is the __________ part of the brain.
(A) largest
(B) smallest
(C) insignificant
Answer:
(A) largest

Question 8.
Each hemisphere of the brain is divided into __________ lobes.
(A) four
(B) six
(C) two
Answer:
(A) four

Question 9.
__________ is called as relay station of the brain.
(A) Hippocampus
(B) Thalamus
(C) Amygdala
Answer:
(B) Thalamus

Question 10.
__________ is called as the pleasure centre of our body.
(A) Hypothalamus
(B) Occipital lobe
(C) Spinal cord
Answer:
(A) Hypothalamus

Question 11.
A protein in the brain called __________ is related to Alzheimer’s disease.
(A) beta-amyloid plaque
(B) thyroxin
(C) gonad
Answer:
(A) beta-amyloid plaque

Question 12.
The spinal cord is connected to the periphery through __________ pairs of spinal nerves.
(A) 25
(B) 13
(C) 31
Answer:
(C) 31

Question 13.
The chemical substances secreted by endocrine glands are called __________
(A) hormones
(B) neurons
(C) axons
Answer:
(A) hormones

Question 14.
Hyposecretion of thyroxin leads to cretinism among __________
(A) old people
(B) children
(C) adults
Answer:
(B) children

Question 15.
In the case of __________, a person loses his weight and experiences irritated mood, sleeplessness as well as sweaty palms.
(A) Myxedema
(B) Acromegaly
(C) Grave’s disease
Answer:
(C) Grave’s disease

Question 16.
__________ is secreted by the pancreas.
(A) Glycogen
(B) Cortisone
(C) Progesterone
Answers:
(A) Glycogen

1B. Match the following pairs.

Question 1.

A	B
i. Spinal cord	a. PNS
ii. Autonomic Nervous system	b. Telodendria
iii. Terminal Button	c. Cerebrum
iv. Reticular Formation	d. CNS
	e. The Alarm clock of the body

Answer:

A	B
i. Spinal cord	d. CNS
ii. Autonomic Nervous system	a. PNS
iii. Terminal Button	b. Telodendria
iv. Reticular Formation	e. The alarm clock of the body

1C. State whether the following statements are true or false.

Question 1.
The human nervous system is amongst all living creatures.
Answer:
True

Question 2.
The autonomic nervous system internal activity of the human body.
Answer:
True

Question 3.
Dendrite is a gap between two neurons.
Answer:
False

Question 4.
Glutamate is the chief inhibitory neurotransmitter.
Answer:
False

Question 5.
The brain consists of five major parts.
Answer:
False

Question 6.
The brain stem is divided into medulla oblongata and pons.
Answer:
True

Question 7.
Medulla oblongata receives messages from higher centers of the brain.
Answer:
True

Question 8.
The reticular activation system is a bridge between two hemispheres.
Answer:
False

Question 9.
Midbrain consists of the superior and inferior colliculus.
Answer:
True

Question 10.
Two hemispheres of the brain are connected by a bundle of fibers called the corpus callosum.
Answer:
True

Question 11.
If a person’s left side of the body is paralyzed, neurons from the left side of his body stop functioning.
Answer:
False

Question 12.
The temporal lobe is in the cortex, just above the ears.
Answer:
True

Question 13.
People who exercise regularly have a higher risk of developing Alzheimer’s disease.
Answer:
False

Question 14.
The human brain consumes 40% of the body’s total energy.
Answer:
False

Question 15.
The spinal cord extends from neck to waist.
Answer:
True

Question 16.
Exocrine glands are also called ductless glands.
Answer:
False

Question 17.
In myxedema, a person becomes very huge, lacks motivation, and complains about weakness.
Answer:
True

Question 18.
The adrenal gland is also known as the sex gland.
Answer:
False

1D. Identify which hormones with hyposecretion or hypersecretion would lead to the following conditions.

Question 1.
Grave’s disease
Answer:
Hypersecretion – Thyroxin

2A. Explain the following concepts.

Question 1.
Nervous system
Answer:
The nervous system is the complex network of neurons that carry signals from brain to body and body to brain. Our nervous system consists of two major parts, viz, the central nervous system and the peripheral nervous system.

Question 2.
Cerebral cortex
Answer:
The cerebral cortex is the grey coloured outside cover of the cerebrum. It controls higher-order mental processes such as attention, perception, learning, and memory.

Question 3.
Reflex action
Answer:
Reflex action is an involuntary and nearly instantaneous movement in response to stimulus, e.g. salivation, sneezing, knee jerk, blinking of eyes. These are quick and simple patterns of behaviour without the involvement of the brain.

Question 4.
Glands
Answer:
Glands are specialized groups of cells or organs that secrete chemical substances. There are many glands. All glands fall into two categories, viz. endocrine and exocrine.

3. Answer the following questions in 35-40 words.

Question 1.
Explain the classification of the somatic nervous system.
Answer:

• The somatic nervous system is divided into sensory and motor systems of the body.
• It consists of sensory nerves (afferent nerves) and motor nerves (efferent nerves). Sensory nerves send messages from the body to the brain and motor nerves send messages from the brain to the body.

Question 2.
Why do we get different reactions to every situation?
Answer:

• When a neural message passes from end buttons to the dendrite of another neuron, it has to cross the chemical gap between two neurons (synapse).
• As neurons are not directly connected to each other, we don’t have fixed reactions to every situation.

Question 3.
State any two functions of the brain.
Answer:

• The brain helps to adapt to the environment and tries to analyze, store and synthesize the information it receives.
• The brain plays a crucial role in every aspect of our lives like decision making, emotional experience, and social interactions.

Question 4.
Why are we supposed to wear helmets while riding a bike?
Answer:

• If someone meets with an accident while riding a bike, the person falls back on his head.
• Most of the time, his Medulla oblongata is damaged which will lead to instant death.
• Hence, we are supposed to wear helmets while riding a bike.

Question 5.
Explain the impact of hypersecretion of any four hormones.
Answer:

• Parathyroxin: An individual experiences a feeling of nausea, vomiting sensation. He also feels sleepy and relaxed.
• Cortin or cortisone: An individual experiences increased sexual drive. Females start looking like males.
• Adrenalin and noradrenaline: An individual experiences increased heartbeat, blood pressure, and breathing rate.
• Androgen and testosterone: An individual shows a tendency towards sexual behaviour. He feels very energetic and engages in aggressive behaviour.

Question 6.
Explain the impact of the hyposecretion of any three hormones.
Answer:

• Parathyroxin: An individual lacks motivation and energy. He experiences weakness, muscle cramps, and spasms.
• Cortin or cortisone: An individual feels very lazy, lacks sexual drive, and experiences loss of hunger and weight.
• Androgen and testosterone: Males do not have a desire for sex and their voice remains childlike.

4. Write short notes.

Question 1.
Nervous system
Answer:

• The nervous system is the complex network of neurons that carry signals from brain to body and body to brain.
• The human nervous system is the most complicated yet highly developed among all living creatures.
• Our nervous system consists of two major parts, viz, the central nervous system and the peripheral nervous system.
• The central nervous system consists of the brain and spinal cord while the peripheral nervous system consists of the somatic and autonomic nervous systems.

Question 2.
Brain and nutrition
Answer:

• Nutrition plays an important role in brain functioning. Nutritional deficiency may lead to neurological problems.
• Despite representing only 2% of the body’s total mass, the human brain consumes 20% of the body’s total energy due. to the increased metabolic needs of human beings.
• Nutrition plays a crucial role during developing years so to optimize the functions of the brain. It is also essential during old age to avoid the degeneration of cells.
• Nutrition enhances brain functioning. It prevents as well as helps in treating neurological disorders.
• As evolution took place, human life became more complicated and demanding. As a result, the need for nutrition by the brain kept on increasing.
• Today human brain is exposed to a high level of stress which results in oxidation, Any food which is high in antioxidants (almonds, dark chocolate, onions, berries, mangoes, seafood) helps to control the ill effects of oxidation.

Question 3.
Spinal Cord
Answer:

• The spinal cord is an important part of the central nervous system. It extends from neck to waist.
• Its main function is to send information from the brain to the body and from to the body to the brain.
• It controls reflex actions like salivation, knee jerk, blinking of eyes.
• The spinal cord is connected to the periphery through 31 pairs of spinal nerves.
• Each spinal nerve is joined to the spinal cord through two routes: the dorsal and ventral routes.
• If dorsal routes are injured, we will not have sensations while if ventral routes are injured, we will not be able to move our body and control reflex actions.

5. Answer in 150-200 words.

Question 1.
Write a note on neurons.
Answer:

• Neurons are specialized networks of cells that transmit messages from the brain to the body and from the body to the brain. They are the basic units of the nervous system.
• A neuron consists of dendrites, axon, cell body, and terminal button or telocentric.
• The cell body is the body of neurons. The nucleus of the neuron absorbs the food and keeps the cell alive.
• The neural message comes in through the dendrites. These are branch-like structures.
• The neural message goes out from the axon of the neuron.
• At the end of the axon, there are end buttons. It is a bulb-like structure containing chemicals known as neurotransmitters.
• Neurotransmitters are chemical messengers. The neural message jumps across the synapse in order to reach the dendrite of another neuron.
• When the neural message is passing through, it excites or inhibits the neurotransmitter in it. This chemical reaction decides our reaction to various situations in life.

Question 2.
Explain any five pillars of better brain functioning.
Answer:

• Physical and mental exercise: Exercise improves blood flow and memory. It also stimulates chemical changes in the brain that improve learning, mood, and thinking.
• Tackling medical problems: Hypertension, diabetes, obesity, depression, head trauma, higher cholesterol, and smoking increase the risk of dementia. One can control and reduce this risk by going for regular health check-ups and taking medication if required.
• Sleep and relaxation: Sleep energizes the brain, improves mood and immune system by clearing wastage and toxins from the body. Practicing meditation and managing stress will help to control the age-related decline in brain health.
• Mental fitness: It improves the brain’s functioning and promotes new brain cell growth. This helps to decrease the chances of developing dementia. A person can keep his brain stimulated by solving puzzles, watching stimulating movies, or learning something new.
• Social interaction: It is good for brain health to spend time with others, participate in stimulating conversation, and stay connected with family and friends. Studies have shown that those who interact more show less decline in their memory.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 6 Stress Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 6 Stress

1A. Complete the following statements.

Question 1.
_____________ stress is referred to as a physical or psychological reaction that may lead to illness.
(A) Medical
(B) Emotional
(C) Psychological
Answer:
(A) Medical

Question 2.
_____________ is the base of four Kleshas.
(A) Avidya
(B) Dvesha
(C) Abhinivesha
Answer:
(A) Avidya

Question 3.
In Sanskrit, mental health is explained as _____________
(A) swasthya
(B) avidya
(C) arogya
Answer:
(A) swasthya

Question 4.
According to the _____________ prefix, ‘EU’ means good.
(A) Greek
(B) Latin
(C) Italian
Answer:
(A) Greek

Question 5.
_____________ is known as good stress.
(A) Hypo stress
(B) Distress
(C) Eustress
Answer:
(C) Eustress

Question 6.
_____________ increases the heart rate, elevates blood pressure and boosts energy supplies.
(A) Adrenaline
(B) Dopamine
(C) Cortisol
Answer:
(A) Adrenaline

Question 7.
Hans Selye’s General Adaptation Syndrome Model consists of _____________ stages.
(A) four
(B) five
(C) three
Answer:
(C) three

Question 8.
Conflict is a _____________ word which means ‘striking two things at the same time’.
(A) Latin
(B) Greek
(C) French
Answer:
(A) Latin

Question 9.
Lewin talked about _____________
(A) valance
(B) psychoanalysis
(C) conflicts
Answer:
(A) valance

Question 10.
In _____________ focused coping strategy, stress is reduced by resolving the conflict through work on the task at hand.
(A) emotion
(B) problem
(C) thought
Answer:
(B) problem

Question 11.
At times, a lack of capacity to achieve the goal urges individuals to readjust their goals. This is known as _____________
(A) withdrawal
(B) compromise
(C) attack
Answer:
(B) compromise

Question 12.
_____________ theory of Psychoanalysis is the base of defence mechanisms.
(A) Freud’s
(B) Selye’s
(C) Webster’s
Answer:
(A) Freud’s

Question 13.
_____________ operates on two energies.
(A) Ego
(B) ID
(C) Superego
Answer:
(B) ID

Question 14.
_____________ is an indirect way to deal with stress.
(A) Psychoanalysis
(B) Problem-focused coping
(C) Defence mechanism
Answer:
(C) Defence mechanism

Question 15.
In _____________, the material can be recalled up to a certain extent.
(A) suppression
(B) repression
(C) sublimation
Answer:
(A) suppression

1B. Match the following pairs.

Question 1.

A	B
i. Avidya	a. Ego
ii. Asmita	b. Repulsion
iii. Raga	c. Ignorance
iv. Dvesha	d. Lust for life
v. Abhinivesha	e. Attraction

Answer:

A	B
i. Avidya	c. Ignorance
ii. Asmita	a. Ego
iii. Raga	e. Attraction
iv. Dvesha	b. Repulsion
v. Abhinivesha	d. Lust for life

1C. State whether the following statements are true or false. If false, correct them. If true, explain why?

Question 1.
Different people deal with stress in different ways.
Answer:
True
Explanation: Different people deal with stress in different ways depending upon their genetic predisposition and environmental conditions.

Question 2.
Dopamine and oxytocin hormones are associated with negative feelings.
Answer:
False
Reason: Dopamine and oxytocin hormones are associated with positive feelings.

Question 3.
Depression is an example of chronic distress.
Answer:
True
Explanation: Depression is an example of chronic distress as it causes constant changes in moods for a long period of time. A depressed person experiences recurrent negative stress.

Question 4.
Hans Selye asserted that stress is always harmful.
Answer:
False
Reason: Hans Selye asserted that the stress of creative and successful work is beneficial whereas that of failure and humiliation is harmful.

Question 5.
External stressors result in peace of mind.
Answer:
False
Reason: External stressors result in frustration, anger, and disappointment.

Question 6.
The value of the goal differs from person to person.
Answer:
True
Explanation: The value of the goal is subjective. A goal may be attractive or unattractive based on whether an individual wants to achieve it or avoid it.

Question 7.
In avoidance-avoidance conflict, an individual is repelled by both goals.
Answer:
True
Explanation: Avoidance-Avoidance conflict involves two unattractive goals with negative values.

1D. Identify the odd item from the following.

Question 1.
Avidya, Arogya, Asmita, Abhinivesha
Answer:
Arogya

Question 2.
Fatigue, Burn out, Depression, Irritability, Anxiety
Answer:
Irritability

Question 3.
Noise, crowding, Strict parents, Weak economic condition, Hunger
Answer:
Hunger

1E. Identify the conflict of motive that is experienced by the person in the following situation.

Question 1.
Ajit likes two cars but he has enough money to buy only one of them.
Answer:
Approach – Approach conflict

Question 2.
Nishant must do his mathematics homework which he dislikes or get a beating from his parents.
Answer:
Avoidance – Avoidance conflict

Question 3.
Sartaj has to choose between two girls for marriage. One is good-looking but boring. The other one is fun but short.
Answer:
Double Approach – Avoidance conflict

Question 4.
Ami would love to buy a new house but it will create a burden on the family’s financial budget.
Answer:
Approach – Avoidance conflict

Question 5.
Shreya has to decide between two appealing destinations for her vacation.
Answer:
Approach – Approach conflict

Question 6.
Rita either has to be late for work or break traffic rules by driving during the red light.
Answer:
Avoidance – Avoidance conflict

Question 7.
Nisha has a choice between two jobs. One is far away but pays well. The other one is close to her house but has no room for advancement.
Answer:
Double Approach – Avoidance conflict

1F. Identify the defense mechanism used in each of the following examples.

Question 1.
Alisha, who was sexually abused as a child, cannot remember the abuse at all.
Answer:
Repression

Question 2.
Ritesh dresses and acts like Spiderman, his favourite superhero.
Answer:
Identification

Question 3.
Suresh hates his neighbour but believes that his neighbour hates him.
Answer:
Projection

Question 4.
Rajesh, who is very aggressive, becomes a football player.
Answer:
Sublimation

Question 5.
Sanjana gets reprimanded by her boss and goes home and fights with her husband.
Answer:
Displacement

Question 6.
Sanket who is cut off from a sports team fantasizes about winning the Olympics.
Answer:
Daydreaming

Question 7.
Shruti is attracted to her sister’s husband but denies this and believes that her sister’s husband is attracted to her.
Answer:
Projection

Question 8.
After being rejected by a prestigious university, Harshil explains that he is glad because he would be happier at a smaller, less competitive college.
Answer:
Rationalization

Question 9.
Neha really admires Priya, the most popular girl in school and tries to copy her behaviour and dressing style.
Answer:
Identification

Question 10.
Three years after being hospitalized, Sonali can remember only vague details about the event.
Answer:
Repression

Question 11.
Angered by her neighbour’s hateful comment, Ekta spanks her daughter for accidentally spilling milk.
Answer:
Displacement

2A. Explain the following concepts.

Question 1.
Stress
Answer:
The word stress is derived from the Latin word ‘stringi’ which means ‘to be drawn tight’. Stress refers to the discomfort experienced by an individual in demanding situations. It arises when an individual is able to mobilize lesser resources than the situation demands.

Question 2.
Leisure
Answer:
Leisure is quality time spent away from work, domestic duties, studies, after a heavily exhausting period. It has relaxing and recreational qualities. We have choice and freedom in our leisure time.

Question 3.
Cortisol
Answer:
Cortisol is the primary stress hormone. It increases sugar (glucose) in the bloodstream, enhancing the brain’s use of glucose and increases the availability of substances that repair tissues.

Question 4.
Stressors
Answer:
Stressors are environmental conditions, external stimuli, or events that cause stress to an organism. There are two types of stressors, viz. internal stressors and external stressors.

Question 5.
Frustration
Answer:
Frustration is a common emotional response related to anger and disappointment. When an individual is highly motivated to achieve something and when his goal-directed behaviour is blocked by an obstacle, it results in frustration.

Question 6.
Id
Answer:
Id is the most primitive storehouse of our biological energy. Id has psychic energy. It operates on the pleasure principle and demands immediate gratification of desires.

Question 7.
Defense mechanisms
Answer:
Defense mechanisms are an indirect way to combat stress. These are the unconscious strategies used to protect the ego from shattering due to unacceptable and harsh reality. It is a stop-gap arrangement that provides some time for the person to come to terms with reality. It is a face-saving device.

2B. Compare and contrast with examples.

Question 1.
Acute distress and Chronic distress
Answer:

• Acute distress is an intense, short-term negative stress while chronic distress is a long-lasting, recurrent negative distress.
• Acute distress occurs when there is a sudden change in routine or when we experience panic or threat, e.g. traffic jam, accident. Chronic distress is the worst type of stress-causing constant changes in routine for a long period of time. e.g. illness of a family member, death of a spouse.

3. Answer the following questions in around 35-40 words each.

Question 1.
What are the effects of hypo stress?
Answer:
Hypo stress is an insufficient amount of stress which is caused when a person has nothing to do at all. Its effects are as follows:

• It leads to boredom.
• It causes feelings of restlessness.
• People become demotivated and unenthusiastic.

Question 2.
What are the ill effects of distress?
Answer:
Distress is a negative type of stress. Its ill effects are as follows:

• Our body is flooded with emergency response hormones such as adrenaline and cortisol.
• It can cause physical conditions like headaches, digestive issues, and sleep disturbances.

Question 3.
Identify the possible reactions to Approach-Avoidance conflict.
Answer:
The three possible reactions to Approach-Avoidance conflict are:

• One may give importance to the positive value.
• One may be very cautious about the negative value.
• One may leave the goal altogether to avoid the situation.

Question 4.
Explain the impact of excessive use of defense mechanisms.
Answer:

• Excessive use of defense mechanisms leads to a habit of escaping from reality and indulgence in falsehood about one’s own self.
• However, reality chases, and sooner or later one has to face it.
• At such a point, the ego is no longer protected and it may lead to symptoms of mental disorders.

4. Write short notes in 35-40 words each.

Question 1.
Anxiety
Answer:

• Anxiety is a state where a person may feel that something is wrong and will experience symptoms like palpitation, rapid heart rate, sweaty palms, and dry throat.
• Two types of anxiety in Freud’s theory are:
  • Neurotic anxiety: Here, id and ego are in conflict with each other
  • Moral anxiety: Here, the superego and ego are in conflict with each other

For your understanding

• Neurotic anxiety comes from the unconscious fear that the basic impulses of the id will take control of the person, leading to eventual punishment from expressing the id’s desires.
• Moral anxiety comes from the superego. It appears in the form of fear of violating moral codes or values, leading to feelings of guilt and shame.

Question 2.
Defense mechanisms
Answer:

• Defense mechanisms are an indirect way to combat stress.
• They are unconscious strategies used to protect the ego from breaking due to unacceptable/harsh reality. It functions as a shock absorber.
• It should be used moderately as its excessive use leads to a habit of escaping from reality.
• Some commonly used defense mechanisms are projection, displacement, and daydreaming.

6. Answer the following questions in 150-200 words each.

Question 1.
Elaborate on the General Adaptation Syndrome model proposed by Hans Selye.
Answer:

• Hans Selye, the father of stress research, introduced the General Adaptation Syndrome (GAS) model in 1936 showing the effects of stress on the human body.
• He asserted that stress is a major cause of disease since chronic distress causes long term chemical changes.
• The GAS model may be defined as the manifestation of stress in the whole body. It consists of three stages:

a. Alarm stage: It is the first reaction to stress. The organism recognizes that there is a danger and prepares to deal with the threat by a ‘fight or flight response. This natural reaction provides energy to the body to deal with stressful situations.

b. Resistance stage: After the initial shock, the body begins to repair itself. In this phase, it remains on high alert for a while. If one overcomes the stress, the body continues to repair itself until the hormone level, heart rate, and blood pressure come to normal. Signs of this stage include irritability, frustration, poor concentration.

c. Exhaustion stage: If stress is not resolved in the resistance stage, a person enters the exhaustion stage. Here, the body’s ability to cope up becomes less. The individual may collapse quickly and the body’s immune system, as well as the ability to resist stress, diminishes. Signs of the exhaustion stage include fatigue, burnout, depression, and anxiety.

Question 2.
Explain aspects of Freud’s psychoanalysis theory.
Answer:
According to Freud’s theory of psychoanalysis, our personality is controlled by three aspects. They are:

• Id: It operates on the pleasure principle and demands immediate gratification of desires. It operates on primary process thinking where logical rules are not applied. It operates on two energies: Libido (sexual energy) and Thanatos (destructive energy).
• Ego: It operates on the reality principle and has better problem-solving abilities as compared to Id. Ego indulges in secondary process thinking and it knows how and when to satisfy desires.
• Superego: It internalizes the moral values of society (do’s and don’ts) and also includes the ‘rights’ and ‘wrongs’ we unknowingly learn from our role models. It helps us to control impulses coming from the Id and makes our behaviour less selfish and more virtuous. According to this theory, our reactions to situations depend upon the interaction of these three systems.

Question 3.
Explain the different types of defense mechanisms.
Answer:
Some of the defense mechanisms described by Dr. Sigmund Freud are as follows:

• Repression: It is an unconscious mechanism employed by the ego to keep disturbing or threatening thoughts outside our conscious awareness. These are the thoughts that would result in feelings of guilt from the superego.
• Displacement: It is the redirection of an impulse onto a less powerful target. A person cannot retaliate against the actual source of anger and so, redirects his anger on a less threatening object.
• Projection: It involves the individual attributing his own thoughts, feelings, and motives to another person.
• Sublimation: It is one of the most adaptive defense mechanisms as it can transform negative anxiety into positive energy. A person uses sublimation to redirect his motivation into more acceptable and productive tasks.
• Identification: Flere, by adopting another person’s mannerisms, language, patterns, etc., a person tries to imitate his character traits and starts behaving like another person.
• Daydreaming: When life appears to be distressing, people often use fantasy as a way of escaping reality. This is called daydreaming.
• Rationalization: It occurs when a person attempts to explain or create excuses for his failure. In doing so, an individual is able to avoid accepting the true cause or reason for his failure.

Some other important defense mechanisms are:

• Denial: It is an outright refusal to admit or recognize that something has occurred or is currently occurring. e.g. alcoholics often deny that their behaviour is problematic.
• Compensation: It means people overachieve in one area to compensate for failures in another. e.g. a student who fails in studies may compensate by becoming a champion in athletics.
• Intellectualization: It works to reduce anxiety by thinking about events in a cold and clinical way. e.g. a person diagnosed with a terminal illness might focus on learning everything about the disease in order to avoid distress and remain distant from the reality of the situation.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 5 Healthy Me – Normal Me Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 5 Healthy Me – Normal Me

1A. Complete the following statements.

Question 1.
A ‘well-adjusted individual’ would indicate a __________ person.
(A) normal
(B) thoughtful
(C) healthy
(D) obedient
Answer:
(A) normal

Question 2.
Getting betrayed but not allowing it to hurt you for long time shows __________
(A) realistic perception of the world
(B) openness to new experiences
(C) high intellectual ability
(D) high self-esteem
Answer:
(A) realistic perception of the world

Question 3.
__________ intelligence is the ability to understand one’s own and others’ emotions.
(A) Emotional
(B) Social
(C) Cultural
(D) Intellectual
Answer:
(A) Emotional

Question 4.
There are __________ components of EI.
(A) 3
(B) 4
(C) 5
(D) 6
Answer:
(C) 5

Question 5.
__________ is your attitude towards yourself.
(A) Self-esteem
(B) Humanistic perspective
(C) Self-awareness
(D) Emotional intelligence
Answer:
(A) Self-esteem

Question 6.
A scale to measure self-esteem was developed by __________
(A) John Mayer
(B) Peter Salovey
(C) Morris Rosenberg
(D) Daniel Goleman
Answer:
(C) Morris Rosenberg

Question 7.
Sometimes traumatic effects continue for a longer period and a person can get __________
(A) burn out
(B) churn out
(C) fag out
(D) dire out
Answer:
(A) burn out

Question 8.
Pinky is 32 years old and still needs her mother to make her hair plaits every day. This is __________ behaviour.
(A) abnormal
(B) normal
(C) well-adjusted
(D) healthy
Answer:
(A) abnormal

Question 9.
Having poor energy levels and thus not being able to perform expected responsibilities on any given day is a sign of __________
(A) low self-esteem
(B) impaired functioning
(C) low confidence
(D) poor emotional intelligence
Answer:
(B) impaired functioning

Question 10.
Childhood memories are linked to __________ perspective.
(A) evolutionary
(B) psychoanalytic
(C) biological
(D) cognitive
Answer:
(B) psychoanalytic

1B. State whether the following statements are true or false and justify your answer with reason.

Question 1.
Today EQ is considered equally important as IQ.
Answer:
True
Explanation: Emotional intelligence is as important as intellectual abilities since it enables a person to live a balanced and happy life.

Question 2.
Being respectful, trusting, and supporting others are components of self-esteem.
Answer:
False
Reason: All these are components of maintaining a healthy relationship with others.

Question 3.
Adolescents face many challenges.
Answer:
True
Explanation: Adolescents face many challenges such as gender identity issues, sexual orientation issues, bullying, etc.

Question 4.
Morris Rosenberg developed the EI model.
Answer:
False
Reason: John D. Mayer co-developed the model of emotional intelligence with Peter Salovey.

1C. Identify the odd item from the following.

Question 1.
Respect, Fairness, Trust, Threatening behaviour
Answer:
Threatening behaviour

Question 2.
Identity crisis, Bullying, Inferiority complex, Genetic problems
Answer:
Genetic problems

1D. Complete the following table.

Question 1.

1. Michel Beldoch	_________________
2. _______________	Self-control
3. Empathy	_________________
4. Self-esteem	_________________
5. _______________	Diathesis
6. Androgynous	_________________
7. _______________	10th October

Answer:

1. Michel Beldoch	Term ‘Emotional Intelligence’
2. Self-regulation	Self-control
3. Empathy	Putting yourself in other’s shoes
4. Self-esteem	Sense of self-worth
5. Predisposition to disorder	Diathesis
6. Androgynous	Display of masculine and feminine traits
7. World Mental Health Day	10th October

2A. Explain the following concepts.

Question 1.
Emotional intelligence
Answer:
Emotional intelligence is the ability to perceive one’s own and other’s emotions, to discriminate among them, and to use that information to guide one’s thinking and action. It includes the ability to control emotions and handle crucial situations in an appropriate way. Individuals with high emotional intelligence are well-adjusted individuals.

Question 2.
Self-regulation
Answer:
Self-regulation refers to controlling the expression of emotions. It is the ability to express oneself appropriately at the right place and the right time. Emotionally intelligent and well-adjusted individuals are able to control their emotions.

Question 3.
Social skill
Answer:
Social skill is the ability to interact well with others. Some important social skills are active listening, verbal communication skills, nonverbal communication skills, leadership, and persuasiveness. Being helpful, respecting other’s opinions, accepting criticism, being positive, etc. also demonstrate good social skills. These skills enable a person to develop healthy relations with others.

Question 4.
Self-esteem
Answer:
Self-esteem refers to the sense of self-worth and personal value. According to Rosenberg, it is your attitude towards yourself. Well-adjusted individuals have high self-esteem.

Question 5.
Cognitive Psychology
Answer:
Cognitive Psychology is an area of psychology that focuses on mental processes such as memory, thinking, problem-solving, language, and decision-making.

Question 6.
Gender identity
Answer:
Gender identity is a perception of one’s own gender which may or may not be corresponding to their birth sex.

3. Write short notes in 50-60 words each.

Question 1.
Components of emotional intelligence
Answer:

• Self-awareness: The ability to be aware of own emotions, wants, motivations, actions, strengths, and weaknesses.
• Self-regulation: Ability to control emotions and restrain inappropriate actions.
• Self-motivation: Ability to push oneself towards a goal that one has set, without any external reward or punishment.
• Social skills: Ability to comfortably and co-operatively interact and communicate with others.
• Empathy: Ability to put oneself in other’s shoes and understand their pain, loss, grief, or distress.

Question 2.
Diathesis model
Answer:

• The diathesis model explains that those who are already genetically predisposed towards a particular disorder, are more likely to show abnormal behaviour if exposed to environmental stress.
• The disorder is a result of both biological factors (nature) and life experiences (nurture).
• Stressful environmental experiences could be childhood abuse, family conflict, divorce, or death.
• The model states that the stronger the diathesis, the lesser is the less stress required to trigger abnormal behaviour.
• Hence, a similar situation leads to different reactions by different people.

Question 3.
Biopsychosocial model
Answer:

• According to this model, abnormal behaviour results from biological, psychological, and socio-cultural factors.
• Biological factors include age, genetics, physical health.
• Psychological factors include mental and emotional health, beliefs, and expectations.
• Sociocultural factors include interpersonal relations and socioeconomic factors.
• If a person who has a biological predisposition towards abnormality, gets to live in a protective and nurturing environment, there are fewer chances of developing abnormal behaviour.
• Conversely, if he is placed in an environment detrimental to his mental and social well-being, he will show abnormal behaviour.

4. Answer the following questions in 150-200 words.

Question 1.
Explain the needs of adolescents.
Answer:
The ten needs of adolescents can be explained as follows:

• I need to understand myself and be myself (self-awareness and independence)
• I need to have fun, enjoy life, and fill my mind and time with good things, (enjoyment and constructive use of resources)
• I need to know that I am important I am called to be a hero, (power and self-esteem)
• I need to love and be loved just as I am. (need to feel wanted)
• I need to have friends and be a friend, (sense of belonging)
• I need to be a part of something with my friends, (sense of belonging)
• I need to have positive role models for my life, (having someone to look up to)
• I need to understand the meaning of my sexuality. (understanding sexual orientation)
• I need to understand the world around me. (awareness of world)
• I need to have a new relationship with Almighty: deep, real, captivating, and foundation of truth. (strong relation with almighty).

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 4 Human Development Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 4 Human Development

1A. Complete the following statements.

Question 1.
The term ‘____________’ means a progressive series of changes that occur as a result of maturation and experience.
(A) Human Development
(B) Personal Growth
(C) Maturity
Answer:
(A) Human Development

Question 2.
____________ refers to the physical changes like increase in size and weight as the age advances.
(A) Maturation
(B) Growth
(C) Development
Answer:
(B) Growth

Question 3.
____________ psychologists study the characteristics and patterns of developmental stages.
(A) Clinical
(B) Developmental
(C) Industrial
Answer:
(B) Developmental

Question 4.
The duration of prenatal period is ____________ to 290 days.
(A) 251
(B) 238
(C) 283
Answer:
(B) 238

Question 5.
The last stage in prenatal period is called ____________ stage.
(A) germinal
(B) fetal
(C) embryonic
Answer:
(B) fetal

Question 6.
The ____________ sleeps for around 18 to 20 hours.
(A) neonate
(B) embryo
(C) foetus
Answer:
(A) neonate

Question 7.
____________ is also called preschool age or age of curiosity.
(A) Early childhood
(B) Infancy
(C) Late childhood
Answer:
(A) Early childhood

Question 8.
Parents call early childhood as ____________ age.
(A) toy
(B) play
(B) pre-gang
Answer:
(A) toy

Question 9.
Educators regard ____________ as a critical period in the achievement drive.
(A) late childhood
(B) early childhood
(C) adulthood
Answer:
(A) late childhood

Question 10.
The rate of adolescent suicide is higher for ____________
(A) girls
(B) boys
(C) transgenders
Answer:
(B) boys

Question 11.
World suicide prevention day is observed on ____________ every year.
(A) 10th September
(B) 8th October
(C) 11th December
Answer:
(A) 10th September

Question 12.
Late adulthood is the time of ‘____________’.
(A) Empty Nest
(B) High achievement
(C) Low curiosity
Answer:
(A) Empty Nest

Question 13.
____________ is associated with forced leisure.
(A) Late adulthood
(B) Old age
(C) Early adulthood
Answer:
(B) Old age

Question 14.
____________ life begins in old age.
(A) Retirement
(B) Relaxation
(C) Depressed
Answer:
(A) Retirement

1B. Match the following pairs.

Question 1.

A	B
1. Prenatal stage	a. Birth to two weeks
2. Neonatal stage	b. 60 years till death
3. Early childhood	c. Six years to 10-12 years
4. Late childhood	d. 40 years to 60 years
5. Adolescence	e. Conception to birth
6. Early adulthood	f. 12-14 years to 20-21 years
7. Late adulthood	g. Two years to six years
8. Old age	h. 21 years to 40 years

Answers:

A	B
1. Prenatal stage	e. Conception to birth
2. Neonatal stage	a. Birth to two weeks
3. Early childhood	g. Two years to six years
4. Late childhood	c. Six years to 10-12 years
5. Adolescence	f. 12-14 years to 20-21 years
6. Early adulthood	h. 21 years to 40 years
7. Late adulthood	d. 40 years to 60 years
8. Old age	b. 60 years till death

1C. State whether the following statements are true or false.

Question 1.
The life of an individual is real and significant just as the geographical age of the earth.
Answer:
True

Question 2.
Growth is a part of development.
Answer:
True

Question 3.
All developmental changes are genetic by nature.
Answer:
False

Question 4.
Growth, maturation, and development are parallel concepts.
Answer:
True

Question 5.
Maturation is dependent on the environment as well as training.
Answer:
False

Question 6.
Infants develop control of the head and face movements within the first two months after birth.
Answer:
True

Question 7.
By the end of the embryonic stage, the zygote gets attached to the wall of the uterus.
Answer:
False

Question 8.
During infancy, rapid physical and motor development takes place.
Answer:
True

Question 9.
Child experiences stranger anxiety in late childhood.
Answer:
False

Question 10.
James Marcia’s approach discusses identity development in adulthood.
Answer:
False

Question 11.
World suicide prevention day is observed since 2003.
Answer:
True

Question 12.
Erikson asserts that people in late adulthood get experiences and society expects them to be more constructive.
Answer:
True

Question 13.
Elderly people have a minority-group status.
Answer:
True

Question 14.
Most stereotypes about old people are favourable to them.
Answer:
False

2. Explain the following concepts.

Question 1.
Write about internal factors affecting human development.
Answer:

• Internal factors affecting human development are basically related to heredity characteristics or genes.
• Some of the internal factors are Predisposition to certain diseases, immunity, over or under secretion of hormones.
• Internal factors determine the inherent physical and mental characteristics of an individual and thereby, have a crucial impact on the development.

Question 2.
Write about external factors affecting human development.
Answer:

• External factors affecting human development are basically related to nature or the environment.
• Some of the external factors are Parental attitudes and expectations, peer group and
  interpersonal relations, mass media, and overall social environment.
• External factors shape the thoughts, attitudes, and beliefs of an individual and thereby, have a significant effect on development.

3. Answer the following questions in around 35-40 words each.

Question 1.
Explain the cephalocaudal principle of development.
Answer:

• The cephalocaudal principle describes the direction of growth and development.
• It states that the development proceeds from the head to toe.
• According to this principle, the child gains control of the head first, then the arms, and then the legs.

Question 2.
Explain the proximodistal principle of development.
Answer:

• The proximodistal principle describes the direction of development.
• It states that the development proceeds from the center of the body to outward.
• This means that the spinal cord develops before outer body parts.
• The child’s arms develop before the hands and the hands and feet develop before the fingers and toes.

Question 3.
State any four changes in infancy.
Answer:

• During infancy, rapid physical and motor development takes place.
• Within two months, the child can turn his head.
• A child can sit and walk with support by nine months.
• The child starts walking independently by around 12 months of age.

Question 4.
Explain any four changes in early childhood.
Answer:

• The child develops control over his muscles.
• The child becomes physically independent.
• The physical territory of the child increases and he automatically learns about social behaviour.
• The child asks a number of questions to others.

Question 5.
Explain any three changes in late childhood.
Answer:

• The fundamental skills of reading, writing, and calculations develop at this age.
• Hand-eye coordination develops along with micro-skills.
• Even cognitive abilities like thinking and reasoning begin to develop.

Question 6.
Explain any two characteristics of late adulthood.
Answer:

• Late adulthood is a time of achievement. Erikson says that at this age people get experiences and society expects them to be more constructive.
• Late adulthood is a time of evaluation where people evaluate themselves by their achievements and previous aspirations.

4. Write short notes.

Question 1.
Characteristics of infancy
Answer:
Infancy ranges from two weeks after birth to two years. The characteristics of infancy are as follows:

• It is a foundation age because many behavioural patterns, attitudes, and emotions develop during this age.
• There is rapid growth and many changes during this stage. These changes are qualitative as well as quantitative.
• Infancy is an age of independence due to control of body movements. It enables an infant to sit, stand and walk, and manipulate objects around him.
• Due to developed interests and abilities, infancy is the age of increased individuality.
• It is the beginning of socialization since the infant goes from being asocial to social.

Question 2.
Adolescence
Answer:

• The age between late childhood and youth is called adolescence. This age ranges between 12-13 years to 19-20 years.
• During this age, rapid physical development takes place. This stage begins with puberty.
• Height and weight of adolescent increases. Menarche in girls and nocturnal emission in boys occur due to the maturation of sex organs.
• Secondary sex characteristics develop during this stage, e.g. breast development among girls, growth of mustache, and pubic hair among boys.
• Also, the search for identity and independence develops among adolescents. Their thoughts are more logical, abstract, and idealistic.
• Adolescents like to spend more time with their friends.
• Adolescents face a number of problems like identity crisis, addiction, and depression.

Question 3.
Old age
Answer:
Old age ranges from 60 years to death. Old people have to adjust to their environment. In some cases, the death of a spouse leads to loneliness, The characteristics of old age are as follows:

• Old age is a period of decline in physical and mental capacities. Individuals in this stage also face certain health issues.
• There are individual differences in the impact of aging.
• Old age is judged by different criteria, e.g. society tends to judge age in terms of physical appearance and activities.
• There are many stereotypes about old people.
• Most stereotypes are unfavourable.
• Elderly people have a minority-group status.
• Aging requires role changes.
• Adjustment is poor during old age.
• The desire to be young is seen in old age.

5. Answer the following questions in 150-200 words.

Question 1.
Explain three prenatal stages.
Answer:
A period between conception till birth is called a prenatal period. During this period, major developmental changes take place in a very rapid manner. This development goes through three stages as follows:

1. Germinal stage: It ranges from conception to two weeks. Within few hours after conception, the zygote starts a journey down the fallopian tube to the uterus; where it begins the process of cell duplication.
In this process, the zygote divides itself into two cells and then goes on duplicating itself. By the end of this period, the zygote gets attached to the wall of the uterus.

2. Embryonic stage: It starts from the third week after conception and continues till the ninth week. It is a time when the mass of cells (embryo) becomes distinct from a human. This stage plays a crucial role in the development of the brain. Almost all internal and external organs develop by the end of this period.

3. Fetal stage: It begins during the ninth week and lasts until birth. This period is marked by more important changes in the brain. The body parts and structures established in the embryonic stage continue to develop during this stage.

Question 2.
Explain the characteristics of adolescence.
Answer:
The age between late childhood and youth is called adolescence. This age ranges between 12-13 years to 19-20 years. The characteristics of adolescence are as follows:

• Adolescence is an important period that has an immediate effect on the attitude and behavior of an adolescent.
• Adolescence is a transitional period, i.e. it is a bridge between childhood and adulthood.
• Adolescence is a period of physical changes.
• Adolescence is an age of challenges. During childhood, the majority of problems are solved by parents and teachers but an adolescent wants to be independent.
• Adolescence is a time for searching for one’s own identity.
• Adolescence is a time of unrealistic ideas. They have a tendency to look at life through rose-tinted glasses and engage in daydreaming. As a result, they face problems like lack of concentration.
• Adolescence is a threshold of adulthood.

Question 3.
Explain Marcia’s approach to identity development.
Answer:
James Marcia’s approach to identity development during adolescence is as follows:

• Identity foreclosure: Here, adolescents just accept others’ decisions about what is best for them. e.g. a doctor’s son becomes a doctor. These adolescents are happy and self-satisfied. They tend to be authoritarian and have a need for self-approval.
• Identity diffusion: Here, adolescents neither explore nor commit to the alternatives. They are socially withdrawn. These adolescents appear carefree but their lack of commitment impairs their ability to form close relationships.
• Moratorium: Here, adolescents explore some alternatives but make no commitments. They experience high anxiety and psychological conflict. They are lively and appealing and seek intimacy with others
• Identity achievement: Here, adolescents explore and search about ‘who they are and ‘what they do’. Teens who have reached this stage tend to be psychologically healthier, higher in achievement, motivation, and moral reasoning.
• Some adolescents shift among all the above-mentioned categories but for most of them identity gels in late teens and early twenties.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 3 Self Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 3 Self

1A. Complete the following statements.

Question 1.
Rentsch and Heffner found __________ categories by which the participants defined themselves.
(A) eight
(B) five
(C) three
Answer:
(A) eight

Question 2.
According to __________, self-concept is the way individual reacts to himself.
(A) Heffener
(B) Symonds
(C) Rogers
Answer:
(B) Symonds

Question 3.
The __________ determines whether the child will be a boy or a girl.
(A) nurture
(B) sex chromosome
(C) heredity
Answer:
(B) sex chromosome

Question 4.
There are __________ major aspects of self.
(A) four
(B) five
(C) nine
Answer:
(A) four

Question 5.
According to Piaget, self-consciousness starts emerging between __________ months.
(A) 15-24
(B) 17-24
(C) 15-22
Answer:
(A) 15-24

Question 6.
Self __________ is an internal dictionary that describes an individual
(A) image
(B) awareness
(C) efficacy
Answer:
(A) image

Question 7.
Maddux defined __________ as ‘what I believe I can do with my skills under certain conditions.
(A) self-efficacy
(B) self-esteem
(C) self-regulation
Answer:
(A) self-efficacy

Question 8.
People from East Asian culture tend to focus on __________ form of self-regulation.
(A) preventive
(B) promotive
(C) passive
Answer:
(A) preventive

Question 9.
__________ self is our inner personality.
(A) Real
(B) Ideal
(C) Own
Answer:
(A) Real

Question 10.
If ideal self and real self-concept is accurate self are __________, our self-concept is accurate.
(A) similar
(B) different
(C) distant
(A) similar

Question 11.
__________ means people recognise and explore their own potential.
(A) Self-actualisation
(B) Self-efficacy
(C) Self-concept
Answer:
(A) Self-actualisation

1B. State whether the following statements are true or false and give a reason for your answer.

Question 1.
Self-concept is defined as a person’s belief in his ability to accomplish some specific goal or a task.
Answer:
False
Reason: Self-concept is defined as the totality of perceptions each person has of themselves.

Question 2.
Between the age of three – twelve, self-concept is defined in terms of a child’s economic background.
Answer:
False
Reason: Between the age of three to twelve, self-concept is defined mainly in terms of sex, age, family, and what the child believes he or she can or can’t do.

Question 3.
Gender identity and gender role are two different concepts.
Answer:
True
Explanation: Gender identity is a biological aspect of self-concept while gender role is psycho-social in nature.

Question 4.
Gender role is an acquired attribute of self-concept.
Answer:
True
Explanation: Gender roles are acquired through imitation and observation of family atmosphere as well as cultural influences.

Question 5.
Body image is a part of self-awareness.
Answer:
False
Reason: Body image is a part of self-image.

Question 6.
Efficacy expectancies represent skills required to complete the goal.
Answer:
False
Reason: Outcome expectancies represent skills required to complete the goal while efficacy expectancies refer to a person’s analysis about whether he has those skills.

Question 7.
To have a healthy self-concept implies to be a highly capable person.
Answer:
True
Explanation: Self-concept is our total image of ourselves. A person who has a healthy and positive image of himself tends to be capable.

Question 8.
The real self represents our dynamic ambitions and goals.
Answer:
False
Reason: Ideal self represents our dynamic ambitions and goals.

Question 9.
A person who has high self-worth can’t tolerate failure.
Answer:
False
Reason: A person who has high self-worth can cope with challenges in life and also tolerates failure and sadness effectively.

2. Answer the following questions in around 35-40 words each.

Question 1.
What is self-concept?
Answer:

• Self-concept is defined as the totality of perceptions each person has of themselves.
• It is also defined as ‘the totality of the complex, organized and dynamic system of learned beliefs, attitudes, and opinions that each person holds to be true about his or her personal existence’.

Question 2.
Explain psychological components that help us to stay socially connected.
Answer:
Heatherton has identified the following psychological components that help us to stay socially connected:

• We must be aware of our actions and evaluate them.
• We must be able to predict other’s reactions to it.
• We must detect any kind of threat or rejection from others.
• We must do something constructive to improve the situation.

4. Write short notes in 50-60 words each.

Question 1.
Self-concept
Answer:

• Self-concept is our total image of us, i.e. it is our total picture of our abilities and traits.
• It is basically a cognitive construct that determines how we feel about ourselves and guides our actions.
• According to Symonds, self-concept is the way an individual reacts to himself.
• There are four aspects of self-concept, viz. How does a person perceive himself? What does he think about himself? How he values himself? and How he enhances or defends himself?
• Our self-concept develops rapidly during early childhood and adolescence. It continues to form and change throughout our life span as we change.

Question 2.
Rentsch and Heffener’s research
Answer:

• Rentsch and Heffner conducted research on the dimensions of self-concept.
• When they asked 20 questions to 200 university students, they found eight categories by which the participants defined themselves.
• Some of the categories were concerned with personal attributes, such as interpersonal characteristics (e.g. I am a student), interest (e.g. I like dancing), personal beliefs (e.g. I am against child abuse), and self-awareness (e.g. I don’t get angry without a valid reason).
• Others referred to the social environments such as ascribed characteristics (e.g. I am a citizen of India) or social differentiation (e.g. I am from another country).
• Although our answers to specific questions related to self-concept can be different, the overall organization of self-concept is common for all.

Question 3.
Steps to develop a positive self-image
Answer:
Self-image is a personal view or mental picture that we have of ourselves.
Some steps to develop a positive self-image are as follows:

• Making a list of one’s positive qualities
• Asking others to describe one’s positive qualities
• Defining achievable personal goals and objectives
• Trying to overcome illogical and irrational thinking
• Avoiding comparing oneself to others
• Developing one’s strengths
• Learning to love oneself
• Giving positive affirmations
• Remembering one’s own uniqueness
• Remembering how one dealt with problems

5. Answer the following questions in 150-200 words.

Question 1.
What is self-image and body image?
Answer:

• Self-image is a personal view or mental picture that we have of ourselves. It is an internal dictionary that describes an individual as being intelligent, funny, kind, etc. It is a collection of an individual’s strengths and weaknesses.
• Self-image is dynamic and changing. We can take steps to develop a healthier and accurate view of ourselves.
• A healthy self-image starts with learning to accept and love ourselves. It also includes being accepted and loved by others.
• Body image is a part of self-image. It goes beyond what we look like or how others see us. It also refers to how do we think, feel, and react to our physical attributes.
• Body image development is affected by cultural images and the influence of family, peers, and others.
• A positive body image contributes to enhanced psychological adjustment while a negative body image leads to maladjustment.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 2 Branches of Psychology Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 2 Branches of Psychology

1A. Complete the following statements.

Question 1.
Online cheating and fraud have led to the development of a branch called __________ Psychology.
(A) Cyber
(B) Social
(C) Cognitive
Answer:
(A) Cyber

Question 2.
__________ psychologists conduct research effective child-rearing practices.
(A) Social
(B) Developmental
(C) Child
Answer:
(C) Child

Question 3.
According to __________, Social Psychology is the scientific study of how an individual’s behaviour is affected by others.
(A) Myers
(B) Freud
(C) Pavlov
Answer:
(A) Myers

Question 4.
Cognitive Psychology concentrates on higher __________ processes such as reasoning and decision making.
(A) emotional
(B) behavioural
(C) mental
Answer:
(C) mental

Question 5.
The __________ psychologist tries to understand the fundamental causes of behaviour.
(A) cognitive
(B) social
(C) experimental
Answer:
(C) experimental

Question 6.
__________ Psychology is concerned with the general problems of the teaching and learning process.
(A) Educational
(B) Clinical
(C) Experimental
Answer:
(A) Educational

Question 7.
__________ Psychology is similar to Clinical Psychology.
(A) Counselling
(B) Industrial
(C) Experimental
Answer:
(A) Counselling

Question 8.
__________ psychologists generally work with the law enforcement department.
(A) Social
(B) Criminal
(C) Abnormal
Answer:
(B) Criminal

Question 9.
__________ psychologists improve preparation for a competitive event.
(A) Sports
(B) Counselling
(C) Cognitive
Answer:
(A) Sports

Question 10.
__________ Psychology is a branch of Industrial Psychology.
(A) Military
(B) Clinical
(C) Consumer
Answer:
(C) Consumer

Question 11.
Air Force Psychologist is specialised in __________ Psychology.
(A) Rehabilitation
(B) Military
(C) Organisational
Answer:
(B) Military

1B. Match the following pairs.

Question 1.

A	B
1. Clinical Psychology	a. School counsellor
2. Educational Psychology	b. Remand home superintendent
3. Industrial Psychology	c. Hypnotherapist
4. Child Psychology	d. Labour welfare officer
5. Social Psychology	e. Ergonomist

Answer:

A	B
1. Clinical Psychology	c. Hypnotherapist
2. Educational Psychology	a. School counsellor
3. Industrial Psychology	e. Ergonomist
4. Child Psychology	b. Remand home superintendent
5. Social Psychology	d. Labour welfare officer

1C. State whether the following statements are true or false.

Question 1.
Today, there are more than 50 branches of Psychology.
Answer:
True

Question 2.
The main aim of applied branches is to develop principles and establish laws for explaining human behaviour.
Answer:
False

Question 3.
Developmental Psychology examines changes across three major dimensions.
Answer:
True

Question 4.
Child Psychology is a theoretical branch of Psychology.
Answer:
True

Question 5.
Social Psychology studies the role of reinforcement in motivating children.
Answer:
False

Question 6.
Cognitive Psychology is concerned with the study of attention and perception.
Answer:
True

Question 7.
Ivan Pavlov conducted experiments on classical conditioning taking dogs as his subject.
Answer:
True

Question 8.
Abnormal Psychology is an applied branch of Psychology.
Answer:
False

Question 9.
Educational psychologists help in preparing relevant curriculum.
Answer:
True

Question 10.
Clinical Psychology is the largest subfield of Psychology.
Answer:
True

Question 11.
Counselling psychologists offer guidance about adjustment issues faced by a person.
Answer:
True

Question 12.
Criminal Psychology is. closely related to Educational Psychology.
Answer:
False

Question 13.
Industrial psychologists help players to maintain their composure.
Answer:
False

Question 14.
There are many career opportunities in Psychology.
Answer:
True

2. Answer the following questions in around 35-40 words each

Question 1.
Explain the nature of questions studied under various theoretical branches.
Answer:

Developmental Psychology	Questions related to changes that happen during the entire life span
Child Psychology	Questions focusing on children and their responses
Social Psychology	Questions focusing on individual’s response to group influence
Cognitive Psychology	Questions focusing on specific cognitive abilities
Experimental Psychology	Questions focusing on laboratory experiments to study human behaviour
Abnormal Psychology	Questions focusing on abnormal behaviour of human beings

Question 2.
State any five goals associated with Sports Psychology.
Answer:
The goals associated with Sports Psychology are as follows:

• Improve preparation for a competitive event.
• Improve focus and concentration skills of sportspersons.
• Improve teamwork and team cohesion.
• Teach relaxation skills to sportspersons.
• Develop self-awareness and increase the motivation of the team.

Balbharti Maharashtra State Board Class 11 Psychology Important Questions Chapter 1 Story of Psychology Important Questions and Answers.

Maharashtra State Board 11th Psychology Important Questions Chapter 1 Story of Psychology

1A. Complete the following statements.

Question 1.
__________ thought that knowledge is acquired through learning and experience.
(A) Plato
(B) John Locke
(C) Wilhelm Wundt
Answer:
(B) John Locke

Question 2.
Wilhelm Wundt introduced the term __________ experience.
(A) conscious
(B) innate
(C) unconscious
Answer:
(A) conscious

Question 3.
Dr. Sigmund Freud was an __________ physician and neurologist.
(A) German
(B) American
(C) Austrian
Answer:
(C) Austrian

Question 4.
__________ behaviour includes directly noticeable reactions and activities.
(A) Covert
(B) Overt
(C) Conscious
Answer:
(B) Overt

Question 5.
Watson established the school of __________
(A) behaviourism
(B) philosophy
(C) psychology
Answer:
(A) behaviourism

Question 6.
The S-O-R Model was developed by __________
(A) John Watson
(B) Sigmund Freud
(C) Plato
Answer:
(A) John Watson

Question 7.
In SOR, Model ‘R’ stands for __________
(A) reaction
(B) response
(C) rigour
Answer:
(B) response

Question 8.
The first Psychology department was established in __________ University.
(A) Mumbai
(B) Calcutta
(C) Delhi
Answer:
(B) Calcutta

Question 9.
National Institute of Mental Health and Neurosciences (NIMHANS) was established in __________
(A) Bangalore
(B) Hyderabad
(C) Chennai
Answer:
(A) Bangalore

Question 10.
Patanjali explained deep thought about Psychology in __________
(A) Yogsutra
(B) Upanishada
(C) Ayurveda
Answer:
(A) Yogsutra

Question 11.
People who have Rajasi qualities are __________
(A) aristocratic
(B) calm
(C) sluggish
Answer:
(A) aristocratic

Question 12.
__________ means understanding the causes of behaviour.
(A) Description
(B) Explanation
(C) Prediction
Answer:
(B) Explanation

Question 13.
__________ comprises of knowledge about the probable outcomes of behaviour.
(A) Explanation
(B) Prediction
(C) Control
Answer:
(B) Prediction

1B. Match the following pairs.

Question 1.

Group ‘A’	Group ‘B’
i. Indian Psychological Association (IPA)	a. 1916
ii. First Psychology department	b. 1925
iii. National Institute of Mental Health and Neurosciences (NIMHANS)	c. 1962
iv. Indian Academy of Applied Psychology (IAAP)	d. 1955
v. Indian Association of Clinical Psychologists	e. 1989
vi. National Academy of Psychology (NAOP)	f. 1968

Answer:
i – b, ii – a, iii – d, iv – c, v – f, vi – e

1C. State whether the following statements are true or false.

Question 1.
Psychology emerged as a separate branch in the 17th century.
Answer:
False

Question 2.
The symbol of Psychology is Ω.
Answer:
False

Question 3.
Logos means a branch of knowledge.
Answer:
True

Question 4.
Wilhelm Wundt was an Austrian Physician.
Answer:
False

Question 5.
Systematic study of Psychology begun in the year 1869.
Answer:
False

Question 6.
The introspection method was introduced by Wilhelm Wundt.
Answer:
True

Question 7.
John Watson conducted research on animal behaviour, child-rearing, and advertising.
Answer:
True

Question 8.
In the S-O-R model, S stands for stimulus.
Answer:
True

Question 9.
During the 1950-1960s, the focus of Psychology shifted to cognitive processes.
Answer:
True

Question 10.
The hospital for mental diseases was set up at Ranchi.
Answer:
False

Question 11.
There are only two Koshas.
Answer:
True

Question 12.
Gunas determine the characteristics of human beings.
Answer:
False

Question 13.
The goal of description relates to ‘Why’.
Answer:
False

1D. Identify the odd item from the following and give reasons for the same.

Question 1.
Stimulus, Response, Organism, Reaction
Answer:
Reaction
Reason: Rest is the symbol in the S-O-R Model.

Question 2.
Rajas, Kapha, Vata, Pitta
Answer:
Rajas
Reason: The rest are the three types of Doshas.

Question 3.
Aristocratic, Idle, Sluggish, Depressed
Answer:
Aristocratic
Reason: The rest relate to Tamasi’s qualities.

Question 4.
Tirthankar, Kabir, Freud, Vivekanand
Answer:
Freud
Reason: The rests are Indian saints and philosophers.

1E. Complete the following table

Question 1.

1. __________ – Knowledge is innate
2. Prof. Narendra Nath Sen Gupta – __________
3. _________ – Lumbini Park Mental Hospital
4. Yama, Pranayam, Samadhi – __________
5. Describe, Explain, Predict, Control – __________

Answer:

1. Plato – Knowledge is innate
2. Prof. Narendra Nath Sen Gupta – First Psychology department, Calcutta University
3. Calcutta, 1940 – Lumbini Park Mental Hospital
4. Yama, Pranayam, Samadhi – Ashtangyoga, Patanjali
5. Describe, Explain, Predict, Control – Goals of Psychology

2. Answer the following questions in 35-40 words

Question 1.
Explain the study of Sigmund Freud.
Answer:

• Dr. Sigmund Freud was the founder of psychoanalysis. He believed that most human motives are hidden.
• He stressed the importance of early childhood experiences and unconscious impulses in shaping adult personality.
• He explained that any major psychological problems in a person’s life have their roots in the early years of life.

Question 2.
Explain the study of cognition.
Answer

• During 1950s and 1960s, the concentration of Psychology shifted from behaviour to cognitive processes.
• Psychologists were interested in studying the various internal processes that trigger a particular responsibility towards the stimulus.
• These processes comprise attention, memory, reasoning, etc. and they play an active role in the cognitive processes.

For your understanding
Cognitive science is the scientific study of human thoughts. It examines mental actions of obtaining information as well as understanding through thoughts, experiences, and senses.

Question 3.
Write a note on Ashtangyoga.
Answer:

• In the fifth century B.C., sage Patanjali described deep thought about Psychology in Yogsutra.
• He developed the theory of Ashtanga yoga.
• The eight aspects of Ashtangyoga are Yama, Niyama, Aasana, Pranayam, Pratyahar, Dharana, Dhyan and Samadhi.
• It helps us to control our wishes and desires.

3. Write short notes.

Question 1.
The latest definition of Psychology
Answer:

• The latest definition of Psychology explains that it is the study of human behaviour and mental processes.
• Important terms in this definition are behaviour, mental processes, and the scientific method.
• Behaviour is the reaction of an organism to various stimuli present in the environment.
• It is either overt or covert. Overt behaviour can be seen directly and includes responses such as walking, talking, dancing while Covert behaviour cannot be seen directly and includes responses such as thinking, feeling, etc.
• The mental processes consist of thinking, memory, forgetting, emotion, motivation, attention, and perception.
• In a scientific study, experiments are conducted in a controlled environment. It enables researchers to study sample populations and generalise certain observations to the entire population.

Question 2.
Doshas
Answer:
According to Ayurveda, there are three types of Doshas; viz. Kapha, Vata, and Pitta.

• Kapha Dosha: Individuals who have Kapha as a dominant Dosha is calm, flexible, patient, and caring. They take a longer time to grasp a subject but have a strong memory.
• Vata Dosha: Individuals who have Vata as a dominant Dosha are unpredictable and moody. They get angry very quickly but they also calm down very fast. They are art lovers,
• Pitta Dosha: Individuals having Pitta as a dominant Dosha are very sharp. They are usually short-tempered.

Question 3.
Gunas
Answer:

• According to Ayurveda, a concept to understand human temperament is called Guna.
• There are three types of Gunas, viz. Sattva, Rajas and Tamas.
• The impacts of Gunas are seen in the behaviour of an individual.
• People with Sattva Guna are calm and understanding. They do their work cautiously and promptly. They are aware of reality.
• People with Rajas Guna are proud and have high self-respect. They are aggressive, (belligerent)
• People with Tamas Guna are idle, sluggish, depressed, and not hard-working.

4. Answer the following questions in detail.

Question 1.
Explain the study of Wilhelm Wundt.
Answer:

• Wilhelm Wundt was a German Physician and Philosopher.
• In the late 19th century, he established the first Psychological laboratory at Leipzig University to study human behaviour.
• He introduced the term conscious experience (i.e. awareness of the mental activities of an organism). This awareness includes the stored mental impressions of the past, present, and future.
• Wundt introduced the Introspection method.
• He also conducted experiments on reaction time, perception, and consciousness. After that, Psychology emerged as a science.

Question 2.
Explain the study of behaviour by John Watson.
Answer:

• John Watson was an American Psychologist who defined Psychology as the Science of human behaviour.
• He conducted research on animal behaviour, child-rearing, and advertising.
• He explained human behaviour through the S-O-R Model.
• Stimulus (S) refers to any physical event or condition that gives rise to a reaction. Organism (0) refers to a human being or an animal, who gives a response to the stimulus. Response (R) refers to the reaction of the organism to a given stimulus.
• Watson also established the school of behaviourism.

Question 3.
Explain Psychology from an Indian perspective.
Answer:

• From 2000 B.C. to 500 A. C., Indian philosophers studied the mind and human behaviour from different viewpoints. They also described ideas like soul, mind, intuition, and so on.
• Upanishads explain the self and personality structure with the help of a concept called Kosha. The different Koshas are Annamaya kosha, Pranmaya kosha, Manomaya kosha, Vidnyanmaya kosha, and Anandmaya kosha.
• Ayurveda explained three types of Doshas; viz. Kapha, Vata, and Pitta and three types of Gunas; viz. Sattva Guna, Rajas Guna and Tamas Guna. Doshas determine characteristics of humans while Gunas explain human temperament.
• In the fifth century B.C., sage Patanjali explained deep thought about Psychology in Yogsutra.
  His theory of Ashtangyoga consists of eight aspects; viz. Yama, Niyama, Asana, Pranayam, Pratyahara, Dharana, Dhyan, and Samadhi. He also studied levels of human consciousness and elaborated on how one can evolve spiritually.
• Many other Indian philosophers and saints also studied the mind and human behaviour.

Balbharti Maharashtra State Board Class 11 Sociology Important Questions Chapter 8 Social Change Important Questions and Answers.

Maharashtra State Board 11th Sociology Important Questions Chapter 8 Social Change

Choose the correct alternative and complete the statements.

Question 1.
Changes in the ………………… of society have an impact on social relationships.
(direction / structure / nature)
Answer:
structure

Question 2.
Changes that take place in several directions at the same time is known as …………………
(linear / multi-linear / cyclical)
Answer:
multi-linear

Question 3.
Styles of dressing which was popular few generations ago have become popular today is an example of ………………… change.
(linear / cyclical / multi-linear)
Answer:
cyclical

Question 4.
………………… compares society to a biological organism.
(Auguste Comte / Herbert Spencer / Max Weber)
Answer:
Herbert Spencer

Question 5.
Social change is …………………, as it denotes a time sequence.
(temporal / complex / immoral)
Answer:
temporal

Question 6.
Giving up social evils like dowry or early marriage is an example of ………………… change.
(long-term / short-term / neutral)
Answer:
long-term

Question 7.
………………… change happens suddenly.
(Planned / Unplanned / Temporal)
Answer:
Unplanned

Question 8.
………………… factor is also known as geographical or natural factor.
(Cultural / Economic / Physical)
Answer:
Physical

Question 9.
The physical environment has also been adversely affected by human behaviour in the name of …………………
(displacement / conditions / development)
Answer:
development

Question 10.
…………….. factor is also known as demographic factor.
(Biological / Physical / Social)
Answer:
Biological

Question 11.
……………….. is defined as the number of females per thousand males in any given population.
(Demography / Sex ratio / Fertility)
Answer:
Sex ratio

Question 12.
………………… development is affected by size of population.
(Socio-psychological / Socio-economic / Socio-cultural)
Answer:
Socio-economic

Question 13.
………………… showed an interrelation between the teachings of Protestant religion and spread of capitalism in Europe.
(Karl Marx / Auguste Comte / Max Weber)
Answer:
Max Weber

Question 14.
……………….. conflict has resulted in class-conflict.
(Social / Economic / Cultural)
Answer:
Economic

Question 15.
The LPG Policy was adopted by the government in …………………
(1971 / 1991 / 1994)
Answer:
1991

Question 16.
………………… development is an index of the overall progress of society.
(Cultural / Technological / Physical)
Answer:
Technological

Question 17.
………………… is a means to help develop ideas, skills, solve problems and transform people.
(Technology / Knowledge / Education)
Answer:
Education

Question 18.
………………… is a statistical study of human population.
(Migration / Demography / Composition)
Answer:
Demography

Correct the incorrect pair.

Question 1.
(a) Herbert Spencer – Functionalism
(b) Emile Durkheim – Theory of Three Stages
(c) Auguste Comte – Protestant Ethic
(d) Max Weber – Organic Analogy
Answer:
(b) Emile Durkheim – Anomic suicide

Question 2.
(a) YCMOU – University Grant Commission
(b) UGC – Right to Education
(c) RTE – Post Globalization
(d) LPG – Yashwant Chavan Maharashtra Open University
Answer:
(d) LPG – Liberalization, Privatization and Globalization

Question 3.
(a) Max Weber – Cultural Factor
(b) Karl Marx – Economic Factor
(c) Demographic Factor – Technological Factor
(d) The Latur Earthquake – Physical Factor
Answer:
(c) Demographic Factor – Biological Factor

Question 4.
(a) Changes takes place everywhere – Universality .
(b) An endless process – Continuous process
(c) It is amoral – Neutrality
(d) Denotes a time sequence – Chain reaction
Answer:
(d) Denotes a time sequence – Temporal.

Identify the appropriate term from the given options.

(Physical Factor, Educational Factor, Economic Factor, Technological Factor, Demography, Biological Factor, Socio-cultural Factor, Unplanned Factor, Information Age, Planned Change, Migration, Interaction Chain Reaction, Long-term Change.)
Question 1.
Consequences of overpopulation and underpopulation.
Answer:
Biological factor

Question 2.
The growth of large scale industries.
Answer:
Economic factor

Question 3.
Online examination.
Answer:
Technological factor

Question 4.
Cultural diffusion is a source of change.
Answer:
Socio-Cultural factor

Question 5.
A huge increase in school fees, will have an impact on student enrolment
Answer:
Interactional factor

Question 6.
Eradicating strongly embedded customs like dowry, sati system, etc.
Answer:
Long-term change

Question 7.
Definite spaces marked for residences, economic zones, parks etc.
Answer:
Planned change

Question 8.
A statistical study of human population.
Answer:
Demography

Correct the underlined words and complete the sentence.

Question 1.
Emile Durkheim has given us a theory of three stages of human thought.
Answer:
Auguste Comte has given us a theory of three stages of human thought.

Question 2.
Human society is a structure with various parts unrelated.
Answer:
Human society is a structure with various parts interrelated.

Question 3.
Joint families are now undergoing significant changes is an example of functional changes.
Answer:
Joint families are now undergoing significant changes is an example of structural changes.

Question 4.
Social changes take place overnight.
Answer:
Social changes take place over time.

Question 5.
Decrease in school fees may further result in higher ‘drop out’.
Answer:
Increase in school fees may further result in higher ‘drop out’.

Question 6.
Social change is immoral.
Answer:
Social change is amoral.

Question 7.
Social programmes have to be immediately designed and implemented for the natural calamities affected person.
Answer:
Rehabilitation programmes have to be immediately designed and implemented for the natural calamities affected person.

Question 8.
Some purposeful and unplanned changes are promoted by the government and other agencies.
Answer:
Some purposeful and planned changes are promoted by the government and other agencies.

Question 9.
Social change is a result of the interaction of single factors.
Answer:
Social change is a result of the interaction of multiple factors.

Question 10.
Technological factors consist of climatic conditions, bio diversity, natural resources, etc.
Answer:
Physical factors consist of climatic conditions, bio diversity, natural resources, etc.

Question 11.
Social change is to some extent conditioned by religious factors.
Answer:
Social change is to some extent conditioned by physical factors.

Question 12.
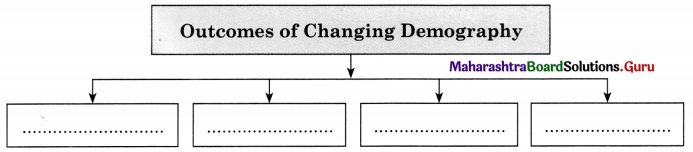
The problems of food, housing, unemployment, poverty are problems as well as direct outcomes of changing sex ratio.
Answer:
The problems of food, housing, unemployment, poverty are problems as well as direct outcomes of changing demography.

Question 13.
Economic competition has resulted in class – conflict, increase in capitalism in the society.
Answer:
Economic competition has resulted in class – conflict, increase in materialism in the society.

Question 14.
For Conflict Theorist, culture is considered a basis for change in society.
Answer:
For Conflict Theorist, conflict is considered a basis for change in society.

Question 15.
One of the benchmarks of a so-called civilized society is its extent of cultural development.
Answer:
One of the benchmarks of a so-called civilized society is its extent of technological development.

Question 16.
The government is taking huge efforts to reach to all sections of society through digitalization.
Answer:
The government is taking huge efforts to reach to all sections of society through Right to Education.

Write suitable examples of the given concepts and justify your answer.

Question 1.
Social change.
Answer:
Example : For example, in today’s ‘Information Age’, the role of a teacher in a school is radically different than it was during the early Vedic period. Structural changes always occur in society. For example, with regard to structure in terms of size of family, joint families are now undergoing significant changes. At the same time there are functional changes in the family system. Education was a function of the family previously. Today it has become a specialized function which has been passed on to schools, colleges through a formal means of education.

Social change is a change in the social structure and social relationships of the society. Society change is a continuous, ongoing process. ‘The term’ social change refers to changes that take place in the structure and functioning of social institutions; for example, government education, economy, marriage, family, religion. Social changes also refers to change in performance of social roles of individuals according to changing times.

Question 2.
Long – term change.
Answer:
Example : Giving up social evils like dowry, early marriage or domestic violence. Eradicating strongly embedded customs and practices take decades to get rid of.

Social changes that may take years or decades to produce results are long – term changes. Significant social changes having long-term effects include the industrial revolution, the abolition of slavery etc. social movements play important role in creating awareness and inspiring discontented members of a society to bring about social change.

Question 3.
Unplanned change.
Answer:
Example : Natural calamities such as famine, floods, earthquakes, tsunami, volcanic eruption, etc. are the instances of unplanned changes. Social change which occurs in the natural course is called the unplanned change. The unplanned changes are spontaneous, accidental or the product of sudden decision.

When a natural disaster takes place, there is a loss of human and animal lives as well as property. Rehabilitation programmes have to be immediately designed and implemented for the affected persons. Unplanned change by its very name suggests that it is a type of change that is not planned. It happens suddenly.

Question 4.
Demography.
Answer:
Example : The study of statistics such as births, deaths, income, or the incidence of disease, which illustrate the changing structure of human populations. The problems of food, housing, unemployment, poor health, poverty, low standard of living etc., are problems as well as direct outcomes of changing demography.

Demography is a statistical study of human population. Demography encompasses the study of the size, structure and distribution of the population. It records spatial and temporal changes in population in response to birth, migration, aging and death. The composition of a particular human population is demography.

Question 5.
Direction of social change.
Answer:
Example : Linear Change – Primitive society moving towards a state of industrialism. Multi-linear Change – Cultural diversity.
Cyclical Change – Styles of dressing or hairstyling which were popular few generations ago have become popular today.

Social change is a change in social structure and social relationship of society. Auguste Comte has given us a theory of three stages of human thought. Society change is a continuous process. Sometimes changes proceed from one stage to another in a single direction known as linear change. It may also be a multi-linear change, that is, changes can take place in several different directions at the same time. Then again, the change may be cyclical, that is, human society goes through certain cycle.

Write short notes.

Question 1.
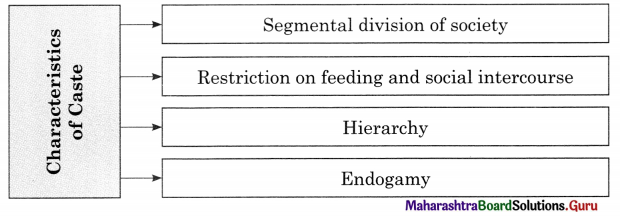
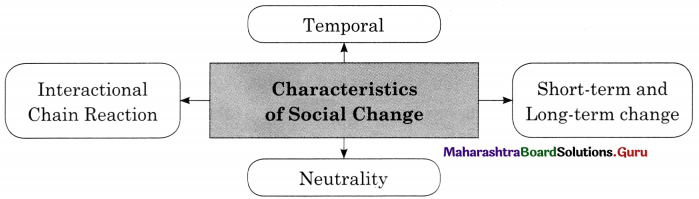
Characteristics of Social Changes.
Answer:
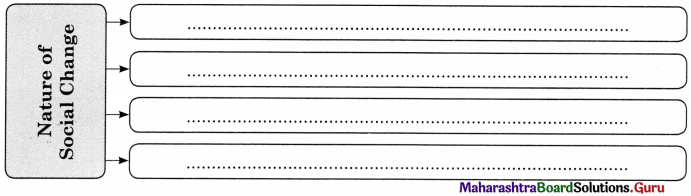
1. Universality : All human societies change. This could include changes in population, beliefs, tools, attire, customs, roles, music, art, architecture etc. Social change is universal as it takes place everywhere. This change is not uniform as it takes place at differing speeds.

2. Continuous speed : There is continuity of change in society. Right from the emergence of human society from the times of nomadic cave dwellers to the present, every aspect of human life and living has changed.

3. Temporal : Social change is temporal as it denotes a time sequence. Innovations of new things, modifications and renovation of the existing phenomena and the discarding of the old takes time.

4. Interactional chain reaction : The physical, biological, technological, cultural, social economic and other factors may together bring about social change. This is due to mutual interdependence of social phenomenon. Thus, for example, a huge increase in school fees will have an impact on student enrolment.

5. Neutrality : The term social change has no value judgment attached to it. As a phenomenon, it is neither moral nor immoral it is amoral. It is ethically neutral.

6. Short term and long-term change : Some social changes may bring about immediate results while some others may take years or decades to produce results. The purchase of new gadgets for the purpose of entertainment is faster if one has the purchasing capacity when compared to giving up social evils like dowry, early marriage or domestic violence.

7. Planned or unplanned changes : Unplanned changes happens suddenly and is not planned. For example, when a natural disaster takes place, there is a loss of human and animal lives as well as property. Rehabilitation programmes, some purposeful and planned changes promoted by the government are examples of planned change.

Question 2.
Socio cultural factor of social change.
Answer:
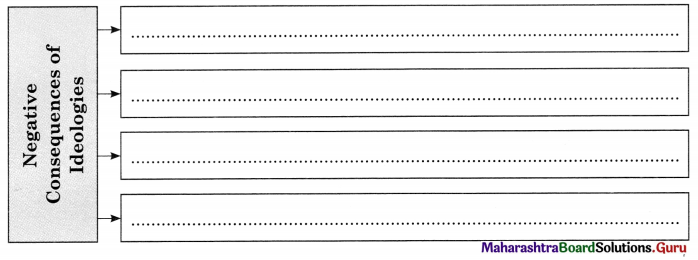
Human culture is a process of change. A change in the cultural order is accompanied by a corresponding change in the whole social order. Cultural diffusion is a source of change. Culture includes our values, beliefs, ideas and ideologies, morals, customs and traditions. These are all subject to change and they in turn, cause changes. Ideas and cultural values play a crucial role in social change.

German sociologist, Max Weber gave importance to the cultural factor of social change. He showed an interrelation between the teachings of protestant religion and spread of capitalism in Europe, in his famous book “Protestant Ethic and the spirit of Capitalism”. Also, these are negative consequences of ideologies that promote religious fundamentalism, extremist thinking, superstitious beliefs and practices, mindless values; these leads to untold hardships and human miseries. They become stumbling blocks to change.

Question 3.
Technological factor of social change.
Answer:
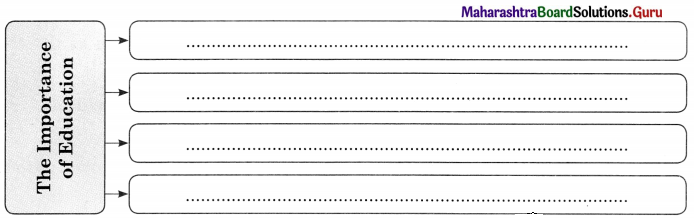
One of the benchmarks of a so called civilized society is its extent of technological development. Technological development creates new conditions of life and new conditions for adaptation. Technological development continues to be an index of the overall progress of society. Technological changes have affected social, economic, religious, cultural and political life of human beings.

Opportunities for e-learning, e-library, e-commerce, e-ticketing, online marketing, online examination is possible today, due to technological innovations. We live in digitalized age. Digitalization has helped the government to identify many beneficiaries who can be provided aid.

Question 4.
Educational factor and social changes.
Answer:
Education is a means to help develop ideas and skills, solve problems, transform people. People acquire knowledge, skills, develop, competencies and then use these to seek employment or self¬employment. The purpose of education, its content, its pedagogy is changing. Use of technology within education though e-learning, online education, smart boards, virtual classrooms, national digital library etc have brought about far reaching changes even within the field of education.

Many persons have opportunities to learn due to the efforts of the government. A special effort has been made by the University Grants Commission (UGC) to encourage education for trans¬gender persons. Educations can transform people lives.

Question 5.
Economic factor and social changes.
Answer:
This factor is of unique importance in social change. Stages of economic development in human history are not limited to economic transformation in society. They promote large scale political and social transformations. Economic development affects different institutions. The growth of large-scale industries led to employment opportunities, professionalism, exploitation, trade unionism and so forth. Economic competition has resulted in class-conflict increase in materialism in the society. The class divide continues to this day.

For example, peasant movement, women’s movements, labour movements, student movement, tribal movement etc. for conflict theorists – conflict is considered a basis for change in society. Globalization as a process continues to have a huge impact on Indian society. The LPG policy adopted by the government of India in 1991 has led to far reaching consequences on our political institutions, economy, family, education etc.

Differentiate between.

Question 1.
Physical and biological factors of social change.
Answer:

Physical factor	Biological factor
(i) Physical factor is also known as geographical or natural factor.	(i) Biological factor is also known as demographic factor.
(ii) Physical factors consists of climatic conditions, physical environment, animal life, biodiversity, mineral resources, natural resources, etc.	(ii) The biological factors lies in the biological conditions of social continuity, the perpetuation, growth or decline of a given population, migration or race.
(iii) Social change to some extent conditioned by physical factors.	(iii) Biological factors bring change in population structure.
(iv) Physical factor is modified by man, to meet his needs for example construction, of bridge, dam, highway, road, canal, irrigation etc.	(iv) Population movement from rural to urban area, and other such demographic changes significantly influence the course of social change in a society.

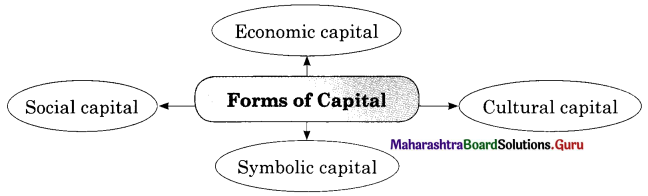
Complete the concept maps.

Identify the significant factor of change for each.
Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

State whether the following statements are true or false with reasons.

Question 1.
Social change is a complex phenomenon.
Answer:
This statement is True.

1. It includes the direction of social change, form of social change, sources of social change, causes of social change, and consequences of social change.
2. Any alternation, difference, modification that takes place in a human situation through time, can be called social change.
3. A single factor may trigger a particular change, but it is almost associated with other factors due to interdependence of several factors which makes social change a complex phenomenon.

Question 2.
Cultural diffusion is not a source of change.
Answer:
This statement is False.

1. Cultural diffusion is a source of change. Culture includes our values, beliefs, ideas and ideologies, morals, customs and traditions.
2. These are all subject to change and they in turn, cause changes.
3. Where two cultures meet or clash, social changes are inevitable.

Question 3.
The physical environment has also been adversely affected by human behaviour.
Answer:
This statement is True.

1. The physical environment has been adversely affected by human behaviour, in the name of ‘development’.
2. The effects of industrial pollution on the environment and the consequent effects such as global warming, melting of solar caps etc., are examples of the physical environment.
3. Hence, there is a need for conscious efforts to promote ‘sustainable development for all’. To solve the problem created by physical environment.

Question 4.
Both, overpopulation or under population has its share of consequences.
Answer:
This statement is True.

1. Both, overpopulation or under-population has its share of consequences.
2. It leads to regional imbalance, changes in density, skewed sex ratio.
3. Socio-economic development and access to opportunities is affected by size of population. For example, the growing population of senior citizens, or declining number of youth in some communities creates new challenges for society.

Question 5.
Economic Factor is of unique importance in social change.
Answer:
This statement is True.

1. Stages of economic development in human history are not limited to economic transformation in society.
2. They promoted large scale political and social transformations. Amidst these changes, there continues to be a need for a decent livelihood and human welfare.
3. Economic development affects different institutions like family, education etc. The growth of large-scale industries led to a spurt in cities, employment opportunities, professionalism, exploitation, trade unionism and so forth.

Question 6.
The purpose of education, its content, is changing.
Answer:
This statement is True.

1. Use of technology within education through e-learning, online education, smart boards, virtual classrooms, National Digital Library etc. have brought about far-reaching changes even within the field of education.
2. Today many persons have opportunities to learn due to the efforts of the government.
3. A special effort has been made by the(UGC) to encourage education for transgender persons.

Question 7.
There is no direction to social change.
Answer:
This statement is False.

1. Sometimes, changes proceed from one stage to another, like in a sequence, and in a single direction.
   For example, Auguste Comtes Theory of Three Stages of human thought is an example of linear change.
2. It may also be multi- linear, that is, changes can take place in several different directions at the same time.
3. Change may also be cyclical; for example, this is common in the world of fashion. Styles of dressing or which were popular few generations ago have become popular today.

Give your personal response.

Question 1.
The consequences of social change may be constructive or destructive.
Answer:
Every factor of social changes has both constructive or destructive results. Physical factors like natural calamities leads to displacement which affects human life. However, geographic condition may also be favourable for human settlements. Similarly, both over population and under population has its share of consequences. Ideas and cultural values also play a crucial role in social change but some ideologies when promote religious fundamentalism and superstitious beliefs does have negative consequences on society. The growth of large-scale industries has not only increased employment opportunities but also have given rise to exploitation.

Question 2.
The purchase of new gadgets for the purpose of entertainment is faster as compared to giving up social evils like dowry, early marriage or domestic violence.
Answer:
Invention and usage of new gadgets is change in material culture. While social evils like dowry, early marriage or domestic violence is strongly embedded customs and practices and part of non¬material culture. Material culture changes fast as compared to non-material culture which are long-term change.

Question 3.
The social system also becomes dysfunctional at times.
Answer:
Emile Durkheim makes reference to ‘anomic suicide’ where there is a state or normlessness or chaos, which can trigger off suicidal feelings which further leads to instability of society. Similarly, there are many other factors which may disturb the balance of the society. Then human beings have to make conscious efforts to help bring about stability, balance and equilibrium in society.

Answer the following question in detail (about 150 words).

Question 1.
Discuss factors responsible for social change with examples of your own
Answer:
More often than not, social change is a result of the interaction of multiple factors.
1. Physical factors : This factor is also known as geographical or natural factor. Physical factors consist of climatic conditions, physical environment, biodiversity, natural resources etc. Social change is to some extent conditioned by physical factors. Natural calamities such as famine or drought affect human lives. The Latur earthquake in 1993, in Maharashtra had long-term impact in terms of displacement. However, geographical conditions may also be favourable for human settlements. For example, people who live in areas which have plenty of rain, suitable soil conditions, rich in minerals have progressed more rapidly.

2. Biological factor : This factor is also known as demographic factor. Biological factors influence numbers i.e., population, sex composition, birth rate and death rate, fertility rate and the hereditary quality of successive generations factors like size and composition of population produce social change. Socio-economic development and access to opportunities is affected by size of population. For example, the growing population of senior citizens or declining number of youths in some communities creates new challenges for society.

3. Socio-cultural factor : Any change in cultural order is accompanied by a corresponding change in the whole social order. Cultural diffusion is a source of change. Ideas propounded by biologist Charles Darwin, psychoanalyst Sigmund Freud and thinker Karl Marx, for example, in the past century, have had significant impact across the globe. Also, there are negative consequences of ideologies that promote religious fundamentalism, extremist thinking, superstitious beliefs and practices which are stumbling blocks to change.

4. Economic factor : Economic development affects different institutions. The growth of large- scale industries led to a spurt in cities, employment opportunities, professionalism, exploitation, trade unionism and so forth. Economic competition has resulted in class-conflict increase in materialism in society. The ‘conflict approached’ as stated by Karl Marx has had a significant impact on understanding social change and also on movements against injustice in society. For example: peasant movement, labour movement, women’s movement etc. Globalization as an economic process continues to have a huge impact on Indian society.

5. Technological factor : One of the benchmarks of a so-called civilized society is its extent of technological development. Technological development continuous to be an index of the overall progress of society. Our daily life is increasingly loaded with the effects of technology from our homes to our work places, entertainment, voting, banking, e-business, e-governance, etc., opportunities for e-learning, online examination is possible today, due to technological innovations.

6. Educational factor: Education is a means to develop ideas and skills, solve problems, transform people. People do acquire knowledge, skills, develop competencies and then use these to seek employment or self-employment. Use of technology within education through e-learning, online education, smart boards, virtual classrooms, have brought about far reaching changes even within the field of education.