Balbharti Yuvakbharati English 11th Digest Chapter 3.2 Blog Writing Notes, Textbook Exercise Important Questions and Answers.
Class 11 English Chapter 3.2 Blog Writing Question Answer Maharashtra Board
11th Std English Chapter 3.2 Brainstorming Question Answer
Yuvakbharati English Navneet 11th Digest PDF Free Download Maharashtra Board
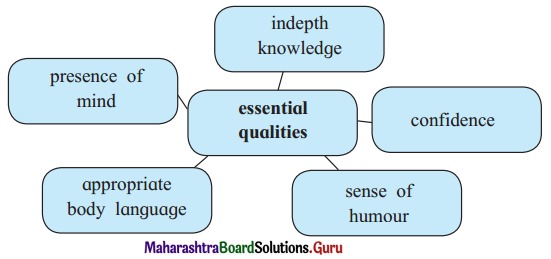
Question (i)
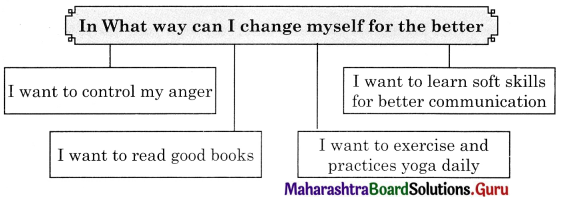
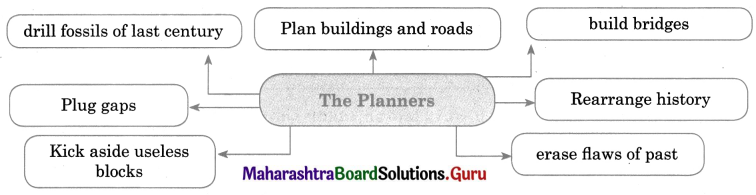
Discuss the various mass media available for people to express their views and complete the web.
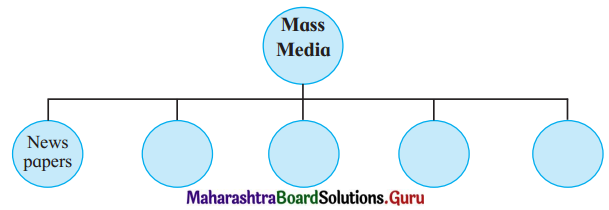
Answer:


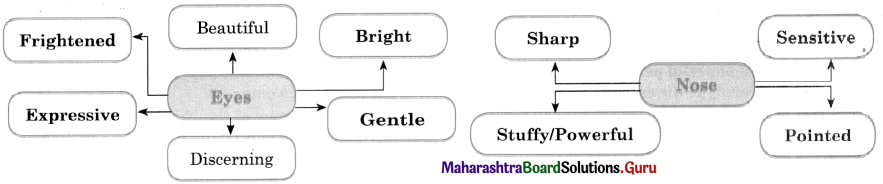
Question (ii)
Discuss the various mass media available for people to express their views and complete the web.
Answer:
|
A
Profession
|
B
Description |
C
Known as
|
| Blog Writing |
Writes/Publishes an information piece, views, opinions, etc. on (www.World Wide Web) |
Blogger |
| Story Writing |
Writes in short on one or more genres of fiction/in magazines, anthologies, etc. |
Story Writer |
| Song/Lyric Writing |
Writes lyrics/songs for films, plays, etc. on a given topic |
Song Writer/Lyricist |
| Academic Writing |
Writes in scientific journals, university magazines, etc., as a result of their Studies and Research |
Academic Writer |
| Translating |
Translates an original work from one language into another |
Translator |
| Newspaper Writing |
Writes in national, state and local newspapers as a staff member |
Journalist |
| Column Writing |
Writes on trends or comments on issues in a column everyday or weekly |
Columnist |
| Screen Writing |
Writes scripts for films/movies/T.V., etc. |
Screenplay Writer |
| Fiction/Novel Writing |
Writes long stories of fiction, non-fiction and other genres |
Novelist |
| Drama/Play Writing |
Writes for theatre on genres like fiction and non-fiction, historical, etc. |
Dramatist/Playwright |
(A1)
Question 1.
Discuss the various blogs and their features with your friends.
A blog helps us to express our –
Answer:
- feelings
- thoughts
- opinions
- views

(A2)
Question (i)
We all know that blogs can be written on any topics. Your teacher will divide the class in groups and assign a task to every group to make a list of various topics on which blogs are normally written. List a few.
Answer:
- Social Awareness
- Environmental Issue
- Health
- Personality Development
Question (ii)
Go through the blog given in the text and also refer to different blogs on the internet about various social issues and environment hazards. Write blogs on the topics given below.
Answer:
(i) Earth with no Trees
Trees are not only our best friends but our life. They are an important part of our ecology as they produce oxygen on which human beings exist. They absorb carbon dioxide and release oxygen which we human beings and wild life breath. There would be no rain if there were no trees. Trees absorb water through roots and release during transpiration. Trees keep environment moist. They help to prevent soil erosion.
Trees also conserve rainwater. Sometimes dead trees fall on the soil and gets buried. It is a scientifically proven fact that trees control sound pollution. This is the reason why trees are planted at the strategic locations like highways, near factories and near airports. Trees conserve energy, save water, shield us from dangerous UV rays.
If there were no trees, there would be no life. We would not get food, clothing, shelter and the most important, oxygen, on which survival depends. There would be no rainfall. Temperature on the earth would increase and ultimately not only human but also life of every small creature would be in danger.
(ii) Say ‘No’ to Tobacco
In India every year about 2 millions die due to tobacco and its effects. It is the biggest enemy of public health. Tobacco is one of the causes of cancer. A smokers puts not only his life but the life of others in danger. Inhaling the smoke from cigarettes, cigars or pipes we too intake tobacco which is hazardous to life. Bronchitis, liver cancer and prostrate cancer are gifts of tobacco. Around 15% of teenagers are addicted to tobacco, it is therefore necessary to create awareness. After all ‘Prevention is Better than Cure’. Creating grassroot level awareness is a must.
Everyone should make an effort to educate youngsters about the ill effects of tobacco. At the same time, there should be government control over sale of tobacco products. Strict action should be taken on companies selling tobacco illegally in remote as well as rural areas. At the same time, strict action also must be taken to reinforce the already existing ban on the sale of tobacco products near educational institutes. Health check-up camp must be organized regularly to detect oral diseases specially cancer. Mass-media should be aggressively used to campaign against tobacco.
(iii) Man vs Nature
Human beings are the creation of nature. Humans get food, clothing water, shelter, air and a ton of other things from nature. Our mother earth is a unique planet where conditions are suitable for life. Breathing is the most necessary and natural action for every moment which depends on the nature. But we are behaving carelessly on the planet. We hurt nature due to our carelessness.
We have set up millions of factories on the earth which create and increase air pollution. Smoke from vehicle is added daily. This causes pollution and affects our health too. At the same time, we go on cutting tress which actually are our best friends. Besides greed for the forest products, humans greed for encroaching forest land for his use is increasing day by day. As a result of it, wild life is also in danger. There are vast reservoirs of pure drinking water on the globe but we are using it carelessly and polluting it.
It has been noted by researches that in coming 50 years there will scarcity of oil. Global warming is hazardous for everyone. It is creating problems to Glaciers. Not only man but other animals are also creations of the nature but we have put their life too in danger. As a result we don’t find the small bird ‘sparrow’ in polluted cities. Actually by keeping this attitude towards nature, man is digging his own grave. Nature is powerful enough to correct hostile actions of human beings. If nature decides to correct human actions, flood, tsunami, famine, anything can be the result. Therefore it is the need of time that humans should live smartly in harmony with nature and respect nature too.
(iv) Child Labour: A Curse to Humanity
Child Labour is a curse to humanity. Children are supposed to go to school, enjoy and learn but are found to be working. They are the most important asset of the society but poverty, illegitimacy, problem of unemployment make them do odd jobs. We are also responsible for this problem of child labour. This problem is more common in underdeveloped nation and thus needs to be corrected.
Protecting children from being child labourers is the responsibility of not only government but of each and every citizen. Use of children as a helping hand on own farm was common but the things changed after industrialization. Various factory owners appointed children and we find many children doing dangerous tasks in industries like fire crackers, carpet industries. In such industries their life is found to be in danger. In pencil making industry they are subjected to lung diseases, In carpet making industries they can lose their eyesight and in fire crackers industry they are exposed to dangerous chemicals. All this must be avoided and banned at the earliest.
To curb this, children from poor strata of the society should be provided with education and teenagers with vocational training. Education will create awareness among them. Some arrangement of providing them nutritious food should also be made by the Government and NGOs. To eradicate the problem of child labour, meticulous planning not only by the government but also by ‘us’ is needed. This is sadly not functioning to the fullest and as a result we share the blame of child labour.

(A3)
Question 1.
Prepare a word register for writing a blog, by choosing a particular topic of your own choice. You can write on environment, pollution, education etc.
Answer:
Word Register – Pollution:
global warming, Co2, breathing, tree plantation, factories, water pollution, air, soil, oxygen, ozone layer, diseases, infection, climate, ultraviolet rays.
Word Register Education:
Knowledge, school, college, vocational, training, personality, awareness, books, internet, apps, computer.
(A4)
Question 1.
Given below are the few topics for blog writing. Discuss and write.
- Personality Development
- Health and Fitness
- Social Dynamics
- Self Defence
- Communication Skills
Answer:
(i) Personality Development:
Personality is a perfect amalgam of a person’s physical and psychological development, manners, relationship with other members of the society, optimistic attitude and many other factors. Now a days management skill including time management, soft skills, health and leadership qualities also play an important role in shaping ones personality.
Practice of Yoga, meditation and regular exercise can keep a person fit. For learning time management one can keep small goals and try to complete the same in a limited time span. We must be polite while speaking with others. Our behaviour should not be aggressive. One must be a good listener and should be proactive rather than being reactive. Creative vision, optimism arise from within. Reading, knowledge about the world matters a lot.
Possessing all these qualities, increase the confidence of the person which is ultimately reflected in his character. Our positive gestures, while speaking, our being social help us to climb the ladder of success. To learn all these qualities, one must keep aside the ego. One should avoid backbiting and should always help others whenever needed. One should be confident enough, always try to learn new things and be one’s ownself. All these qualities cannot be achieved overnight. Some of these come from within while some can be achieved. Including all these qualities in a person’s character creates a good personality.
(ii) Health and Fitness
It is said that ‘Health is wealth’. Health in medical term does not only mean free of diseases but it also means a state of being well. A healthy person should be able to do his daily chores, his occupation. A healthy or physically fit person is able to face changes in the surrounding.
Health and fitness can be achieved by various ways such as intake of nutritious diet, healthy lifestyle, maintenance of hygiene, regular exercise or yoga and meditation. Not only this but a person’s positive attitude towards life matters the most. Proper and nutritious diet can keep you physically fit but meditation and yoga along with optimistic attitude keep one mentally fit. Regular practice of yoga and mediation reduces stress, blood sugar level and various other health issues like blood pressure and hyperacidity.
Now a days almost all human beings including kids are found to be under stress. Industrialization and computerization has no doubt made human life easy but created many health and fitness issue. There is a competition in every walk of life and one must survive the same. The basic need is therefore to stay healthy and fit. One can achieve it by going to gym, practising yoga and meditation, running, walking, cycling, aerobics, dance, swimming, playing outdoor games and many others. Practising any of these is the key of maintaining health. To maintain health and fitness has now become a need of the time.
(iii) Self Defence
Self defence means defending oneself from getting harmed. Physical self defence is the use of force for self protection. One can protect himself by being armed or unarmed too. Armed self defence allows the use of weapons for self defence while in unarmed self defence person does not use any weapon. His only weapon is his stamina and physical strength. There are some restrictions on the use of weapons. The armed force is the exception to it. Not only this, but self defence can also be achieved by avoiding the problematic situation.
Self defence techniques can be learned and learning the same is an urgent need of in today’s age. Specially women must learn it. In the changing scenario of increasing terrorism in society, it becomes a necessity for everyone to learn it. Many martial arts coaches train their students various methods of self defence. Apart from learning self defence, one must be optimistic enough to handle the problems in front of him. While handling the critical situation, everyone should trust in themselves and tackle with high level of confidence.
(iv) Social Dynamics
Man is a social animal. He lives in a society and is influenced by the people around him.. Our society is built on the principles of social dynamics. In society, behaviour of every person is different. People interact with one another and this results in deciding their behaviour in a group. Thus social dynamics is actually a behaviour of group which is the result of influence created by other group members. Social dynamics involve the study of interrelationship of people with one another.
When people come together in a group,they interact, share their thoughts, their ideas and knowledge. The exchange of thoughts, knowledge and ideas bring about positive change in the group behaviour, thereby bringing change in the society.
(v) Communication Skills
The way of communicating to others is an important skill in a person which enables us to understand the things that are being said. Our brains develop at every stage of our life using different techniques to communicate a message. There are many different skills used to communicate a message in an effective manner.

The principles of effective communication are Listening, Speaking when required, Curiosity, Engaging and Body language. Using the principles of effective comm unication helps increase our ability to be understood. This boosts our confidence and self esteem to speak.
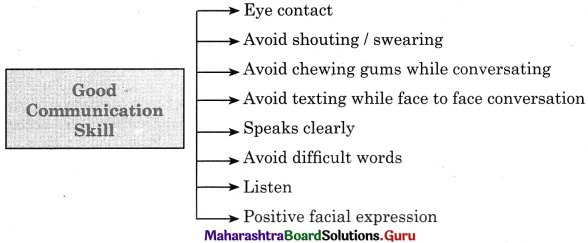

(A5)
Question 1.
There are many blog websites like www.livejournal.com, www.wordpress. com, www.blogger.com and www.blogs.myspace.com. You can develop your blog writing skills taking on the basis of this make a list of career opportunities available to you.
Yuvakbharati English 11th Digest Chapter 3.2 Blog Writing Additional Important Questions and Answers
Question 1.
What is the importance of blog writing?
Answer:
A blog is an article on a topic expressing the views, experiences or feelings of a person. Writing a blog is really a challenging thing to do.
In the changing scenario of E-age, we find that joint families are rarely seen. Even in nuclear families now a days family members hardly share their views, ideas. (The reason may be any.) People are in contact with each other but are not connected. In such situation a blog plays very important role.
A blog gives a platform to the person to share his views, opinion or even feelings. In this way he gets an opportunity to communicate with people. Secondly in spite of availability of mass media like newspaper, writing of a person cannot be published always. A blog provides a person (blogger) to share his views and make it available for the readers. One can share anything interesting in a blog.

Question 2.
What is the difference between a blog writing and newspaper write up?
Answer:
A blog is an article wherein a person (a blogger) has right to share his views feelings or opinion about anything. A newspaper article writer does not share his feelings or views always. A newspaper article is generally focused on the topics of public interest. Most of the time newspaper articles are only informative. A newspaper article can be written daily or weekly whereas a blogger can write and post a blog at any time in a day.
Question 3.
What precaution is taken while developing a blog?
Answer:
A blog is an article expressing person’s views, feelings or opinion. Utmost precautions should be taken while posting a blog on social media. There is no limitation regarding number of words and number of topics on which a blog can be written. But a blogger must make sure to avoid repetition. A reader may find it uninteresting to read lengthy description of a simple thing.
A blog posted on social media is read by many people belonging to different caste, creed and community. A blogger must not post anything in his blog which may 1 hurt feelings of people or make antisocial elements active.
Question 4.
Why is a blog developed and uploaded?
Answer:
A blog is a platform one gets to express his views, feelings or opinions. A person a blogger) can communicate with the world through his writing. Writing a blog is an opportunity given to mature writers. A blogger can refine his writing skills while expressing his views. It is uploaded so that he can communicate and share his experiences with others. It can give a chance to the blogger to be a good writer.

Question 5.
Go through the blog given in the text and also refer to different blogs on the internet about various social issues and environment hazards. Write blogs on the topics given below.
Answer:
(i) Are we Happier than our Forefathers?
There was a time centuries ago, in the stone age when man wandered about from place to place in groups. Slowly life became stable, when man decided to settle down. He learnt farming and domestication of animals like cow, sheep, goat and buffalo. These animals gave him milk and helped him to plough the field as well as carry loads. This change in man was a definite change for the better.
Of course, today the world has progressed by leaps and bounds. Quick means of communication, advancement in technology, the boon of the atomic age has made distances so small. The world today has become a smaller place, thanks to progress.
Medicines and drugs have lengthened life and given us cures for dreaded disease. Today man can do so many things that our forefathers could not even dream of achieving. Excessive use of fuels such as diesel, kerosene, petrol and other harmful chemicals have ruined the planet earth. Our atmosphere is so steeped in poisonous gases that we have no fresh air to breathe. This has resulted in the depletion of the ozone layer. Atomic weapons and bombs are a constant threat to our very existence.
Do we honestly say we are happier than our forefathers? At what cost? Yes, we are more comfortable, we have progressed, but at what cost? At the cost of our lives and happiness. Let us not forget that happiness does not depend on material comforts. It depends on the state of our mind. I can safely say that we have forfeited our mental happiness for worldly comforts.
(ii) If Trees Could Talk
Tree can speak to you and I may not understand what they are trying to tell us. It was proved by the famous scientist, Jagdish Chandra Bose, that plants can feel pain and can even reveal how they are feeling. Unfortunately, these sounds cannot be understood by man and can only be recorded on a graph. Vegetation is not deaf and dumb, though we may think so.
If trees could speak, they would have told us several things both good and bad. I am sure the bad things would be much more than about the good habits of man. I am sure the tree would grumble and cry. out in pain at man’s indecent, vulgar and rude behaviour.
All trees would complain about the brutal and barbarious behaviour of man. A tree would explain to us that it gave us shade from the hot blistering sun, plenty of wood, choicest fruit, medicinal herbs, ayurvedic pesticides and insecticides like the neem, yet man is so ungrateful and despicable, he takes the tree for granted and does not care if he chops it and hacks it painfully.
Man goes about cutting down forests and building high rise structures or big factories that give out poisonous gases. Trees, if we could only understand what they were trying to tell us, would inform us that we were murderers and butchers who took pleasure in destroying nature that God has created for man. They would have wept with grief and pain as they related the insanity and callousness of man.
(iii) Leisure – It’s Uses and Abuses
I remember W. H. Davis saying in one of his poems
‘What is this life, if full of care,
We have no time to stand and stare?!
These lines tell us that in the middle of rushing here and doing this and that and attacking this job and completing that duty, we must ,find time to relax and.cool down. Those of us living in cities spend all our free time, glued to the TV – The idiot box as our elders call it. The rich spend their time in restaurants and nightclubs. No one today spends time with Nature – especially those living in towns and cities.
The best way to spend one’s leisure moments is to come in contact with nature in a park, a zoo, a garden or an aviary. Some of us have a tendency of misusing our leisure time. Some youngsters spend their time gambling, drinking, teasing girls, stealing, getting into trouble by making fun of passers-by and by gossiping. All these activities cause terrible harm to themselves as well as to others. Those belonging to rich families have stag parties or kitty parties and drink alcohol, gamble and go about spoiling the names of their acquaintances and friends.
We can use our leisure time developing our hobbies such as photography, reading, writing, gardening, doing embroidery, painting, learning dancing, playing musical instruments and other things for which we have talents. It is better to develop our talents, for who knows when these will help us in our life. Relaxation is important, but just lying idle will cause trouble to our minds as well as to our body, hence we must do something constructive and useful in our leisure hours.
(iv) Democracy – The Best form of Government
Abraham Lincoln described democracy as the Government of the people, for the people and by the people. This system of government is the most acceptable because every single individual in the country is a part of the governing process. The legislature is elected by the people themselves, while the Executive is selected from the Legislature. A corrupt government will surely not be elected again.
Other forms of government are monarchy and dictatorship. In both monarchy and dictatorship, the ruler is the Supreme ultimate power over the people. The people themselves have absolutely no say in the matter. They have no remedy against misuse of power or against in justice. There is no individual freedom, no freedom of speech or expression. The individual is a captive in his own nation. How ironical this may seem, but it is very true.
I am not saying that democracy is the most ideal form of Government. It does not guarantee social justice and is quite often corrupt. It is slow in functioning and not very capable in emergencies, but yet we feel it is the most effective form of Government.
How can there be an effective function of governments like monarchy, dictatorship and autocracy when the individual is left out completely? Such governments profess ‘might’ is right theory and are more often than not, corrupt and evil one man shows.
The most important attribute of democracy is the fact that all are treated equally before the law, irrespective of caste, creed and sex. The dignity of man is recognised and respected. The individual takes active part in the governing of his country. He is responsible if things go wrong. We therefore feel that democracy is more advantageous than other forms of governments.
(v) Unity in Diversity
India is a land where we can clearly see Unity in Diversity. This means that there is a strand of oneness running through all of us that makes us one in mind and spirit and thought.
India is diverse in topography. We have in one country snow capped mountains as well as deserts, plains as well as plateaus, rivers as well as lakes, areas of heavy rainfall as well as very scanty rainfall. Yet India is one country to all of us. India is a land of diverse people. There are people living in different states who have different language, different mode of dressing different food habits and different traditions. Yet they are all Indians.
We have people of different religions living together as brothers. These external difference of physical features of dress, of language, of food and of festivals are superficial differences to the true Indian. What really matters in the feeling of being an Indian. The strand of Indianness, is what really matters. It is this strand that brings in all Indians the feeling of belonging, the feeling being at home with your near and dear ones.
Today sadly, there is an atmosphere of intolerance, narrow – mindedness, groupism and party spirit, but yet we can proudly say that we have not lost our basic values. The sense of national unity is a priority with most Indians. We must however strive for this unity to be strengthened. We must instill in our youth the feeling of pride for our culture and tradition and we must remember to retain our identity as Indians.
(vi) Students and Discipline
Discipline is of utmost importance in society and it is the student who needs it most if he is going to become an exemplary citizen. Today physical fitness is not all. The student must be taught values and the meaning of discipline in order to make him whole in body and mind. If he is not disciplined from the very beginning he will turn out dissatisfied with life, a failure, and a candidate for violence.
Let us not forget, that teaching discipline to the student is not solely the job of the school. Parents have to be very much involved in this. It is they who have to maintain discipline at home and in the neighbourhood.
We notice that the problem of indiscipline becomes worse as the student grows older and goes to college. This must be because he is now getting more and more exposed to media. TV soaps and other serials and the cinema are always portraying students as indisciplined. They are shown as not having any regard for their elders and betters. Our children love to ape, hence they copy all the bad habits and examples of indiscipline.
Students are becoming more and more violent today. We do not say that they have no reasons to have grievances. Of course, they are not satisfied with the syllabus. They are unhappy with the way teaching is done. They are worried about stiff competition. They are bothered about the free pattern and the partiality of the teachers. These are serious grievances, but this does not mean that students should retaliate by being indisciplined. The education system needs to be changed and our young students must be taught how to choose between right and wrong. A well-disciplined person will become a success in life.
11th Std English Questions And Answers:
![]()
![]()
![]()
![]()