Issue of Shares 12th Secretarial Practice Chapter 3 Solutions Maharashtra Board
Balbharti Maharashtra State Board Class 12 Secretarial Practice Solutions Chapter 3 Issue of Shares Textbook Exercise Questions and Answers.
Class 12 Secretarial Practice Chapter 3 Exercise Solutions
1A. Select the correct answer from the options given below and rewrite the statements.
Question 1.
___________ refers to capital made up of Equity and preference shares.
(a) Share capital
(b) Debt capital
(c) Reserve fund
Answer:
(a) Share capital
Question 2.
___________ capital refers to maximum capital a company can raise by issuing shares.
(a) Issued
(b) Authorised
(c) Paid up
Answer:
(b) Authorised

Question 3.
___________ means shares are offered to the public.
(a) Rights Issue
(b) Private Placement
(c) Public Issue
Answer:
(c) Public Issue
Question 4.
Under ___________ method, issue price of shares is based on bidding.
(a) Book Building
(b) Fixed Price
(c) Bonus Issue
Answer:
(a) Book Building
Question 5.
In ___________, shares of a company are offered to the public for the first time.
(a) Further Public Offer
(b) Initial Public Offer
(c) Public Offer
Answer:
(b) Initial Public Offer
Question 6.
___________ is offered to existing equity shareholders.
(a) IPO
(b) ESOS
(c) Rights Issue
Answer:
(c) Rights Issue

Question 7.
Bonus shares are issued free of cost to ___________
(a) existing Equity shareholders
(b) existing employees
(c) Directors
Answer:
(a) existing Equity shareholders
Question 8.
___________ are offered to permanent employees Directors and Officers of a company.
(a) Bonus Shares
(b) Rights Issue
(c) ESOS
Answer:
(c) ESOS
Question 9.
Under ___________, a company offers its securities to a select group of persons not exceeding 200.
(a) Private Placement
(b) IPO
(c) Public Offer
Answer:
(a) Private Placement
Question 10.
The ___________ have the power to allot shares.
(a) Director
(b) Board of Directors
(c) Company Secretary
Answer:
(b) Board of Directors

Question 11.
Letter of ___________ is sent to applicants who have been given shares by the company.
(a) Regret
(b) Renunciation
(c) Allotment
Answer:
(c) Allotment
Question 12.
___________ is a proof of title to Shares.
(a) Share Certificate
(b) Register of Member
(c) Letter of Allotment
Answer:
(a) Share Certificate
Question 13.
The gap between two calls should not be less than ___________
(a) 14 days
(b) One month
(c) 21 days
Answer:
(b) One month
Question 14.
Company can ___________ shares on non-payment of calls.
(a) forfeit
(b) surrender
(c) allot
Answer:
(a) forfeit
Question 15.
Voluntarily giving away one’s share to another person is called as ___________ of shares.
(a) Transfer
(b) Transmission
(c) Surrender
Answer:
(a) Transfer

Question 16.
___________ of shares takes place due to operation of law.
(a) Forfeiture
(b) Allotment
(c) Transmission
Answer:
(c) Transmission
1B. Match the Pairs.
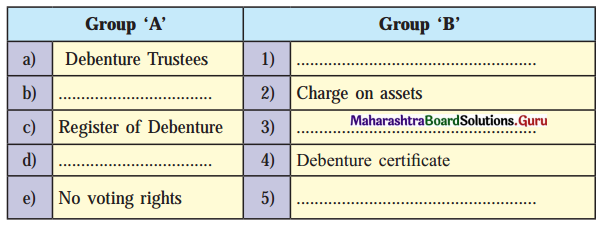
Question (I).
Answer:
| Group ‘A’ |
Group ‘B’ |
| (a) Death of member |
(5) Transmission of shares |
| (b) Voluntary return of shares to company by member |
(4) Surrender of shares |
| (c) Price of shares mentioned in prospectus |
(7) Offered to existing Equity Shareholders |
| (d) ESPS |
(3) Offered to existing employees |
| (e) Regret Letter |
(6) Non-allotment of shares |
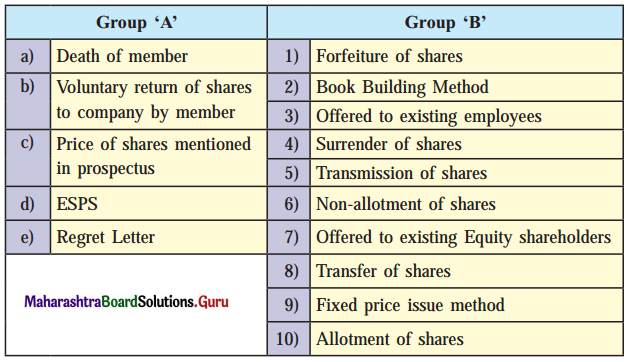
Question (II).
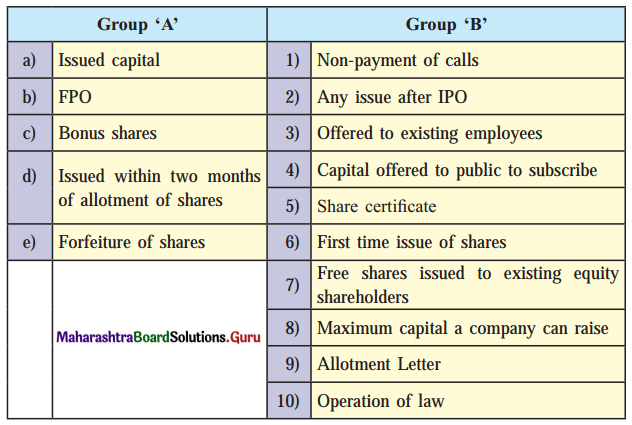
Answer:
| Group ‘A’ |
Group ‘B’ |
| (a) Issued capital |
(4) Capital offered to public to subscribe |
| (b) FPO |
(8) Maximum capital a company can raise |
| (c) Bonus shares |
(7) Free shares issued to existing equity shareholder |
| (d) Issued within two months of allotment of shares |
(5) Share Certificate |
| (e) Forfeiture of shares |
(1) Non-payment of calls |
1C. Write a word or a term or a phrase which can substitute each of the following statements.
Question 1.
Capital collected by way of issue of Equity and Preference shares.
Answer:
Share Capital
Question 2.
Part of issued capital subscribed by investors.
Answer:
Subscribed capital
Question 3.
Capital that will be collected only at the time of winding up of a company.
Answer:
Reserve capital
Question 4.
Highest bid price in Book Building method.
Answer:
Cap price

Question 5.
Offering of shares by a company to the public for the first time.
Answer:
IPO
Question 6.
Subsequent issue of shares after an IPO.
Answer:
FPO
Question 7.
Pre-emptive right given to existing Equity shareholders to subscribe to new issue of shares by company.
Answer:
Rights issue/shares
Question 8.
It is also called as ‘Capitalization of Profits’.
Answer:
Bonus shares
Question 9.
Appropriation of shares to an applicant.
Answer:
Allotment of shares
Question 10.
Committee set up to decide the formula for allotment of shares in case of over-subscription.
Answer:
Allotment committee
Question 11.
Minimum amount to be collected from subscribers within thirty days of issue of prospectus.
Answer:
Minimum subscription

Question 12.
Document which is a prima facie evidence of ownership of certain shares of a company.
Answer:
Share certificate
Question 13.
Penal action taken by company on non-payment of calls.
Answer:
Forfeiture of shares
Question 14.
Person to whom transferor is transferring the shares.
Answer:
Transferee
Question 15.
Transfer of shares due to operation of law.
Answer:
Transmission of shares
1D. State whether the following statements are true or false.
Question 1.
Only fully paid-up shares can be forfeited.
Answer:
False
Question 2.
The member transferring shares is called a transferor.
Answer:
True
Question 3.
A share certificate is issued for partly or fully paid up shares.
Answer:
True
Question 4.
Allotment of shares must be done within one month of receipt of application money.
Answer:
False

Question 5.
Sweat Equity shares are offered to Directors or employees of a company.
Answer:
True
Question 6.
Bonus Shares are issued at a discounted price to the Equity Shareholder.
Answer:
False
Question 7.
The floor price is the highest bid price under the Book Building method.
Answer:
False
Question 8.
Calls not paid by shareholders are called calls in arrears.
Answer:
True
Question 9.
Shares not offered to the public for subscription are called subscribed capital.
Answer:
False
Question 10.
Authorized capital is mentioned in the capital clause of the Memorandum of Association.
Answer:
True
1E. Find the odd one.
Question 1.
Authorized capital, Equity share capital, Issued capital, Paid-up Capital.
Answer:
Equity share capital
Question 2.
ESOS, ESPS, Rights Shares, Sweat Equity.
Answer:
Rights Shares

Question 3.
Floor Price, Cap Price, Cut-off price, Face Value.
Answer:
Face Value
Question 4.
Bonus Shares, Rights Shares, ESOS.
Answer:
ESOS
Question 5.
Allotment of Shares, Forfeiture of shares, Surrender of shares.
Answer:
Allotment of shares
1F. Complete the sentences.
Question 1.
Share Capital refers to capital made up of Equity shares and ___________
Answer:
Preference Share
Question 2.
Reserve capital is part of ___________
Answer:
Uncalled Capital
Question 3.
Transfer of shares due to death, insolvency, or insanity of the member is called ___________
Answer:
Transmission Shares

Question 4.
The two parties involved in transfer of shares are transferor and ___________
Answer:
transferee
Question 5.
Voluntarily giving up of shares by a member due to inability to pay calls is called as ___________
Answer:
surrender of shares
Question 6.
Company can forfeit only ___________ paid shares.
Answer:
partly
Question 7.
In case the original Share Certificate is torn or mutilated, company can issue ___________
Answer:
Duplicate Share Certificate
Question 8.
In case of transfer of shares, the company has to issue to the transferee a new share certificate within ___________
Answer:
one month
Question 9.
Letter sent to applicants for informing them shares are allotted is called as ___________
Answer:
Letter of Allotment

Question 10.
When applications received is more than the number of shares offered, it is called as ___________
Answer:
Over Subscription
Question 11.
In Book Building Method, the final price at which shares are offered to investors is called as ___________
Answer:
Cut-off price
Question 12.
Shares issued free of cost to existing Equity shareholders is called as ___________
Answer:
Bonus Shares
1G. Select the correct option from the bracket.
Question 1.
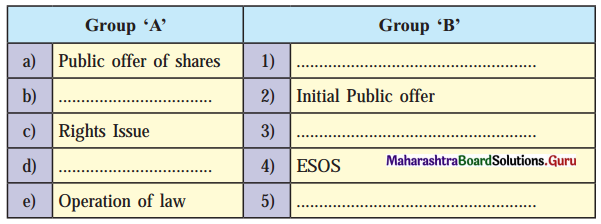
(The first-time offer of shares, Shares offered to the public, Shares offered to exist, Equity shareholders, Shares offered to exist, employees, Transmission of shares)
Answer:
| Group ‘A’ |
Group ‘B’ |
| (a) Public offer of shares |
(1) Shares offered to Public |
| (b) First time offer of shares |
(2) Initial public offer |
| (c) Rights Issue |
(3) Shares offered to existing equity share holders |
| (d) Shares offered to existing employees |
(4) ESOS |
| (e) Operation of law |
(5) Transmission of Shares |
1H. Answer in one sentence.
Question 1.
When does the transmission of shares take place?
Answer:
Transmission of Shares takes place on death, insolvency, or insanity of the members.
Question 2.
Name the two parties involved in the transfer of shares.
Answer:
The transferor and Transferee are the two parties involved in the transfer of shares.

Question 3.
What is the time limit to issue a share certificate on allotment of shares?
Answer:
Secretary should issue share certificate within two months of allotment of shares.
Question 4.
What is the time limit for Filing a Return of Allotment with the Registrar on the allotment of shares?
Answer:
Secretary has to file a ‘Return of Allotment’ with the Registrar of Companies within 30 days of allotment of shares.
Question 5.
When can a company forfeit shares?
Answer:
If a shareholder fails to pay calls on shares within a certain period company can forfeit shares.
Question 6.
What is a share certificate?
Answer:
Share Certificate is a registered document issued by a company that is evidence of ownership of a specified number of shares of the company.
Question 7.
What is the minimum application money to be collected by Company as per the Companies Act?
Answer:
As per the companies act, the company should collect a minimum of 25% of the nominal value of shares.
Question 8.
To whom should the prospectus be filed before issuing it to the public?
Answer:
The prospectus should be filed with the Registrar of Companies before issuing it to the public.

Question 9.
What is meant by private placement?
Answer:
When a company offers its securities to a select group of persons not exceeding 200, it is called Private Placement.
Question 10.
To whom is Sweat Equity shares offered by a company?
Answer:
Sweat equity shares are issued to directors or employees of the company.
Question 11.
To whom can a company issue Bonus Shares?
Answer:
The company can issue Bonus Shares to its existing equity shares.
Question 12.
What is the subsequent issue after IPO called as?
Answer:
The subsequent issue after IPO is called FPO.
Question 13.
Name the method under which the issue price of shares is fixed through a bidding process.
Answer:
Under the Book Building method, the issue price of shares is fixed through a bidding process.
Question 14.
What is Public Issue?
Answer:
Public issue or offer means offering the shares to the public. The company invites the public to subscribe to its shares by issuing a prospectus.

Question 15.
Name the capital which is mentioned in the capital clause of the Memorandum of Association.
Answer:
Authorized Capital is mentioned in the capital clause of the Memorandum of Association.
1I. Correct the underlined words/and rewrite the following sentences.
Question 1.
Issued capital is the maximum capital that a company can raise by issuing shares.
Answer:
Authorized capital is the maximum capital that a company can raise by issuing shares.
Question 2.
Under the Fixed-Price issue method, the price of shares is fixed through a bidding process.
Answer:
Under Book Building Method the price of shares is fixed through a bidding process.
Question 3.
FPO refers to offering shares to the public for the first time.
Answer:
IPO refers to the offering of shares to the public for the first time.
Question 4.
Only Fully paid up shares can be forfeited.
Answer:
Only Partly paid-up shares can be forfeited.
Question 5.
Bonus shares are offered to existing employees of a company.
Answer:
Bonus shares are offered to existing shareholders of a company.
Question 6.
The company enters into an underwriting agreement with the shareholders.
Answer:
The company enters into an underwriting agreement with the underwriters.

Question 7.
Letter of Allotment is sent to applicants when no shares are allotted to them.
Answer:
Letter of Regret is sent to applicants when no shares are allotted to them.
Question 7.
IPO refers to the offering of shares to the public for the second time.
Answer:
FPO refers to offering shares to the public for the second time.
Question 8.
A duplicate share certificate must be issued within one month from the date of application.
Answer:
A duplicate share certificate must be issued within three months from the date of application.
Question 9.
Call money can not exceed 5% of the nominal value of shares.
Answer:
Call money can not exceed 25% of the nominal value of shares.
1J. Arrange in proper order.
Question 1.
(a) Forfeiture of shares
(b) Calls on shares
(c) Allotment of shares
Answer:
(a) Allotment of shares
(b) Calls on shares
(c) forfeiture of shares
Question 2.
(a) Share certificate
(b) Allotment letter
(c) Application from
Answer:
(a) Application form
(b) Allotment letter
(c) share certificate

Question 3.
(a) Return of allotment
(b) Application form
(c) Minimum Subscription
Answer:
(a) Minimum subscription
(b) Application form
(c) Return of allocation
2. Explain the following terms/concepts.
Question 1.
Transmission of shares.
Answer:
- Transmission of shares means the transfer of the title of shares by the operation of law.
- When the shares of a member are automatically transferred to another person on the death, insolvency, or insanity of a member it is called Transmission of shares.
- Transmission of shares is an involuntary action.
- There is only one party i.e., a legal heir who indicates the process of transmission.
- The legal heir or official receiver need not pay any consideration for the shares.
- There is no need to submit an Instrument of Transfer of pay stamp duty.
Question 2.
Bonus shares
Answer:
- Bonus Shares are shares distributed by a company to its current shareholders as fully paid shares free of charge.
- The Bonus Shares are given to the existing equity shareholders according to their existing proportion of equity shareholdings.
Question 3.
Allotment of Shares
Answer:
- Allotment means the distribution of shares among the applicants. It means giving shares to share applicants of to specific persons with whom the company has entered into the contract.
- Allotment of shares is a procedure in which shares are distributed to those applicants who have submitted a written application along with the application money.

Question 4.
Employees Stock Option Scheme
Answer:
An employee stock option plan is an employee benefits scheme under which the company encourages its employees to acquire ownership in the form of shares. Under this scheme, permanent employees, Directors or Officers of the Company or its holding company or subsidiary company are offered the benefit or right to purchase the equity shares of the company at a future date at a predetermined price.
Question 5.
Surrender of Shares
Answer:
- This means the voluntary return of shares by the member to the company for cancellation.
- Surrender of shares is allowed only if there is no other option but to forfeit the shares.
- Only partly paid-up shares can be surrendered.
- Surrendered shares can be surrendered when a company provides for such surrender of shares.
Question 6.
Sweat equity shares
Answer:
These are shares issued by a company to its directors or employees at a discount or for consideration other than cash. It is one of the modes of making share-based payments to employees. It is issued in recognition of their valuable contribution to the prosperity of the company.
Question 7.
Share Certificate
Answer:
A Share certificate refers to documents that are issued by a company evidencing that a person named in such certificate is the owner of the shares of the company stated in the share certificate. Share certificate has to be issued under the common seal of the company. It should be issued within 2 months from the date of allotment against the allotment letter.
Question 8.
Authorized Capital
Answer:
- The Authorized capital is the maximum amount of capital that a company can raise through the issue of shares to the shareholders.
- The Authorized capital of a company is also called Registered Capital or Nominal Capital.
- Authorized capital is the maximum capital that is authorized by the company’s memorandum of Association.

Question 9.
Forfeiture of shares
Answer:
If a shareholder, who is called upon to pay any call fails to pay the amount, even after sending many reminders the company may forfeit its shares. Thus forfeiture of shares means cancellation of shares.
Question 10.
Paid-up capital
Answer:
- Paid-up capital is the amount of money a company has received from shareholders in exchange for shares.
- It is the total amount of money paid up by the shareholders when the company has called up or demanded them to pay.
- The paid-up capital can be equal to or less than the authorized capital.
Question 11.
Calls on Shares
Answer:
- Whenever a company issue shares, the company may ask shareholders to pay the value of shares in installment which is known as calls on shares.
- The company can demand part or full amount of the balance amount of unpaid shares.
Question 12.
Subscribed Capital.
Answer:
- Subscribed share capital is that part of issued share capital for which a company has positively received a subscription from the investor.
- It is a part of Issued Capital that has been subscribed by investors or purchased by the general public.
Question 13.
Minimum Subscription
Answer:
Minimum subscription means a minimum amount decided by the ROC which should be build-up by the company by issuing securities to the general public. If the company failed in minimum subscription then it has to return the entire amount back to the applicants.
Question 14.
Transfer of shares
Answer:
- Transfer of shares means the transfer of ownership of the shares from one person to another against consideration.
- Transfer of shares is effected by removing the name of the existing shareholders (transferor) from the register of members and inserting the name of the new member (transferee).
- Transfer of shares is a voluntary process of transferring shares by a member of a company.

Question 15.
Initial Public Offer (IPO)
Answer:
The initial public offering is the sale of equity shares to the public first time in order to raise capital. This is the most popular and common method used by companies. The company invites the public to subscribe to its shares by issuing prospects.
Question 16.
Blank Transfer
Answer:
- The Blank transfer means the sale or transfer of securities in which the name of the buyer or transferee is not recorded.
- When a member signs the Instrument of transfer without filling in the name of the transferee and hands it over to the transferee with the share certificate it is called ‘Blank Transfer.’
- The blank transfer enables easy to purchase and sale of shares as the blank transfer form can be sold any number of times.
- The intermediate buyers need not pay stamp duty.
Question 17.
Further Public Offer (FPO)
Answer:
It is also called a follow-on public offer. When the company issue shares to the public after IPO, it is called a further public offer. Thus every issue of shares by a listed company after its IPO is called an FPO. FPO leads to an increase in the subscribed capital of the company.
Question 18.
Forged Transfer
Answer:
- An instrument on which if the signature of the transferor is forged is called forged transfer.
- It is a null transfer and does not counter any title.
- As the signature of the transferor is forged, the company should not register such transfer of shares.
Question 19.
Rights issue
Answer:
A rights issue is an invitation to existing shareholders to purchase additional new shares in the company. A rights issue is a way by which a listed company can raise additional capital.

Question 20.
Private Placement
Answer:
When a company offers its securities to a selected group of persons not exceeding 200, it is called private placement. Here securities are not offered to the general public.
5. Study the following cases and express your opinion.
1. Eva Ltd. Company’s capital structure is made up of 1,00,000 equity shares having a face value of ₹ 10/- each. The company has offered to the public 40,000 equity shares and out of this, the public has subscribed for 30,000 equity shares. State the following in rupees-
Question (a).
Authorized capital
Answer:
The authorized capital is ₹ 10,00,000 (1,00,000 equity shares × ₹ 10/- each)
Question (b).
Subscribed capital
Ans. The subscribed capital is ₹ 3,00,000 (30,000 equity shares × ₹ 10/- each)
Question (c).
Issued capital
Answer:
The issued capital is ₹ 4,00,000 (40,000 equity shares × ₹ 10/- each)
2. TRI. Ltd company is a newly incorporated public company and wants to raise share capital by issuing equity shares in the market. The board of directors is considering various options for this. Advise the board on the following matters:
Question (a).
What should the company offer – IPO or FPO?
Answer:
The Company should offer IPO.

Question (b).
Can the company offer Bonus shares to raise its capital?
Answer:
The company cannot offer Bonus Shares. Bonus Shares are given out of only accumulated capital or reserves only.
Question (c).
Can the company enter into an underwriting Agreement?
Answer:
Yes. The company can enter into an Underwriting Agreement. The underwriters assure the company to take up the unsold shares so that company can be able to raise the minimum subscription.
3. Silver ltd. The company has recently come out with its public offer through FPO. Their issue was over-subscribed. The board of directors now wants to start the allotment process.
Question (a).
Should the company set up an allotment committee?
Answer:
Yes. The company should set up an allotment committee as the issue is over-subscribed so the Board has to set up an allotment committee.
Question (b).
How should the company information to whom the company is allotting shares?
Answer:
The company should inform the applicants through a letter of allotment for allotting shares.
Question (c).
Within what period should the company issue a share certificate?
Answer:
The company should issue share certificates within two months from the date of allotment.
4. Red Tubes Ltd. has made a demand on its shareholders to pay the balance unpaid amount of ₹ 20/- per share (having a face value of ₹ 100) held by them. The company has sent letters asking the shareholders to pay the money to its Bankers within the specified time.
Question (a).
Are the shareholders liable to pay ₹ 20/- for the shares held by them?
Answer:
Yes. The shareholders are liable to pay ₹ 20 for the shares held by them. When a company demands the shareholder to pay a part or full amount of the balance amount unpaid on shares it is called ‘calls on shares’.

Question (b).
Name the letter sent by the company to its shareholders asking them to pay ₹ 20/-
Answer:
The company will send a ‘Call Letter’ to its shareholders for asking them to pay ₹ 20.
Question (c).
What happens if the shareholders fail to pay the money within a specific time?
Answer:
If a shareholder fails to pay call money within the specified time, the company can forfeit the shares.
5. X owns 100 shares and Y owns 500 shares of RED tubes. The company has asked all its shareholders to pay the balance unpaid amount of rupees 20. X pays full money demanded by the company and Y failed to pay the money due to poor financial condition.
Question (a).
Can the company forfeit the shares of Y?
Answer:
Yes. The company can forfeit the shares of ‘Y’ as he failed to pay calls on shares within a certain period.
Question (b).
Can the company forfeit the shares of X?
Answer:
The company cannot forfeit the shares of ‘X’ as he paid the full amount of shares. Only partly paid-up shares can be forfeited.
Question (c).
Can X transfer his shares?
Answer:
Yes. X can transfer his shares by filling Instrument of transfer.
4. Distinguish between the following.
Question 1.
Initial Public Offer and Further Public Offer
Answer:
| Points |
Initial Public offer |
Further Public offer |
| 1. Meaning |
IPO refers to an offer of Securities by an unlisted public company to the public for the first time. |
FPO means an offer of securities by a listed public company to the public to raise subsequent capital. |
| 2. Raising Money |
Raising Money for the first time from the public. |
Before FPO Company has already raised money through an IPO. |
| 3. When Issued |
It is usually issued by an existing company that wants to raise capital from the public for the first time. |
It is usually issued by a listed public company when it wants to raise further capital from the public. |
| 4. Order of Issue |
IPO precedes FPO. IPO is the first time sale of shares to the public. |
FPO is always done after IPO. FPO is the second or subsequent sale of shares to the public. |
| 5. Listing |
The company has to get itself listed for the first time before issuing IPO. |
A company making an FPO is already a listed company. |
| 6. Risk |
It is very risky for the investor as he cannot predict the company’s performance. |
It is less risky for the investor as he has an idea of the company’s past performance and can judge its future performance. |
Question 2.
Fixed Price Issue Method and Book Building Method
Answer:
| Points |
Fixed Price Issue Method |
Book Building Method |
| 1. Meaning |
Under this method, the issue price of shares is mentioned in the prospectus and investors have to buy shares at that price only. |
Under this method, the issue price is determined by a bidding process. |
| 2. Price of Shares |
The exact price of shares is known in advance and it is mentioned in the prospectus. |
The price of shares is not known in advance only the minimum price and maximum price at which the company is willing to sell the shares is known in advance. |
| 3. Prospectus |
The company has to issue a prospectus and it contains the details of the price at which shares are offered and the total number of shares offered by the company. |
The company issues a Red Herring Prospectus. It contains only the price band and the total size of the issue. |
| 4. Determination of Demand |
The company comes to know the public demand for its shares only after the closure of the issue. |
The company comes to know the public demand for its shares every day. The bids are registered in the book .everyday till the closure of the issue. |
| 5. Payment of Application Money |
Application money or entire money has to be paid by the investor at the time of submitting the application for shares. |
Only application money has to be paid at the time of bidding. Money will be collected only after the issue price has been fixed. |
| 6. When Used |
It can be used for any issue i.e., Public issues, Rights Issues, FSOS, etc. |
It is usually used in public issues i.e., IPO and FPO |
Question 3.
Right shares and Bonus shares
Answer:
| Points |
Rights Shares |
Bonus Shares |
| 1. Meaning |
In the rights issues, shares are offered to the existing equity shareholders. |
Bonus shares are issued to the existing equity shareholders free of cost. |
| 2. Payment |
Subscribers have to pay for the Right Shares. |
Bonus Shares are issued free of cost to the shareholders. |
| 3. Partly/Fully paid-up shares |
Shareholders have to pay for these shares as Application Money, Allotment, Call money, etc. |
Bonus Shares are fully paid up shares so no money has to be paid by shareholders to the company. |
| 4. Minimum Subscription |
The company has to obtain a minimum subscription for Rights shares. |
There is no minimum Subscription to be collected for Bonus shares. |
| 5. Right to Renounce |
The shareholders can renounce their shares. |
Shareholders cannot renounce their bonus share. |
| 6. Purpose of Issue |
The main purpose to issue rights shares is to raise fresh funds and along with it to give a chance to their existing members to increase their shareholding. |
The main purpose of issuing bonus shares, is to give rewards to its existing equity shareholders out of its accumulated huge profits or Reserves. |
Question 4.
Transfer of shares and Transmission of shares
Answer:
| Points |
Transfer of shares |
Transmission of shares |
| 1. Meaning |
Transfer of shares means the transfer of ownership of shares from one person to another by entering into a contract. |
It means the transfer of ownership of a member’s shares to his legal representative due to the operation of law. It takes place on the death of insolvency or insanity of the members. |
| 2. When Done |
It is done when the member wants to sell his shares or give his shares as a gift. |
It is done when the member dies or becomes insolvent or suffering from insanity. |
| 3. Nature of Action |
It is a voluntary action taken by the member. |
It is an involuntary action. It is performed by operation of law. |
| 4. Parties Involved |
In the transfer of shares, there are two parties involved – the member who is called as transferor and the buyer who is called as transferee. |
There is only one party e.g., the nominee of the members in case of death of the member or the legal representative. |
| 5. Instrument of transfer |
Transfer requires an Instrument of transfer. |
No instrument of transfer is needed. |
| 6. Initiated by |
The transferor initiates the transfer process. |
Legal representative or official receiver initiates the process of transmission. |
| 7. Consideration |
Transfer of shares is done often by the member to receiving some consideration e.g., money. |
In the transmission of shares, no consideration is involved. |
| 8. Liability |
The liability of the transferor ends after the shares are transferred. |
Original liability of the member continues in case of transmission of shares. |
| 9. Stamp duty |
Stamp duty as per the market value of shares has to be paid. |
No stamp duty is to be paid. |
5. Answer in brief.
Question 1.
What is Book Building Method?
Answer:
- The method of offering shares by providing a price range is called the book building method.
- In the book, building method shares will be sold by the bidding process.
- The company issues a Red Herring Prospectus which contains a price range or price band and as the investor to bid on it.
- In this method, the company doesn’t fix up a particular price for the share but gives a price range e.g., ₹ 80 to ₹ 100.
- When bidding for the shares, investors have to decide at which price they would like to bid for the shares e.g. ₹ 80, ₹ 90, ₹ 100.
- The lower price band (₹ 80) is known as the floor price and the highest price band (₹ 100) is known as the cap price. The final price at which shares are offered to investors is called the cut-off price.
- Board on the demand and supply of the shares, decides the final price is to be fixed.
- Investors can bid on any number of shares that they are willing to buy at a given price band. Such Bidding is kept open for 5 days.
- The bids with application money are to be submitted to the Lead Merchant Bankers called ‘Book Runners’ who enter the bids in a book.
- After bidding, the company fixes a cut-off price at which shares on offer can be sold.
- The company issues a prospectus that contains the final price.
- Book Building method is used for public issues i.e., IPO and FPO.

Question 2.
State the provisions for the Rights issue.
Answer:
- When a company wants to issue further capital it can issue shares to its existing equity shareholders which are called Rights Issue.
- According to the Companies Act, 2013 company has to fulfill certain provisions for making a Rights Issue.
- the provisions are
- Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
- A company has to send a ‘Letter of offer’ to the existing shareholders at the time of issuing Rights Shares.
- The letter of offer shall mention
- The number of shares offered.
- The period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of offer.
- The letter of offer can be sent by registered post, speed post, courier, or through electronic mode.
- If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and the company can offer the unsold shares to new Investors.
Question 3.
State the provisions related to Bonus Shares.
Answer:
- Bonus Shares are fully paid shares issued free of cost to the existing equity shareholders.
- According to Companies Act 2013, every company has to follow certain provisions to issue Bonus Shares.
Following are the provisions related to Bonus Issue-
- A company can issue Bonus Shares only out of
- Free reserves or
- Securities Premium Account
- Capital Redemption Reserve Account
- A company cannot issue Bonus Shares only out of Reserves credited by the Revaluation of Assets.
- It also cannot issue Bonus Shares instead of paying dividend.
- Once the announcement for Bonus Shares is made by the Board of Directors, it cannot be then withdrawn.
- Bonus shares are fully paid up shares.
- Shareholders cannot renounce i.e give away their Bonus Shares to another person.
- There is no minimum subscription to be collected.
Question 4.
State the general principles/rules for allotment of shares.
Answer:
Every company issuing shares has to follow rules or general principles given by the Companies Act 2013 as follows:
- Proper Authority: The Board of Directors or the allotment committee set up by the Board has the authority to allot shares.
- Allotment must be against application only: A Company can allot shares only if it has received a written application for shares from the applicant. Allotment of shares cannot take place on the basis of an oral request.
- Reasonable time: As per the Act, allotment shall be done within 60 days of receipt of application money. Allotment can be made from the fifth day from the date of issue of prospectus.
- Absolute and Unconditional allotment: Shares should be allotted on the same terms as stated in the prospectus and application form. No change in terms of allotment or new conditions can be added at the time of allotment.
- Communication: Company has to inform the applicant that shares have been allotted, to him by sending a letter of allotment or allotment advice. The letter gives details of a number of shares allotted amount of Allotment money to be paid etc.
- Allotment should not be in Contravention (Violation) of any other laws: A company cannot allot shares by violating or contradicting any other existing laws e.g., shares cannot be allotted to a minor, of a country where a company operates its business.

Question 5.
State the contents of the Share Certificate.
Answer:
A Share certificate refers to a document which is issued by a company evidencing that a person named in such certificate is the owner of the shares of the company stated in the share certificate.
Share certificate has to be issued under the common seal of the company. It should be issued within 2 months from the date of allotment against the allotment letter.
Contents of Share Certificate:
Share Certificate should be in Form SH – 1 as prescribed under Companies (Share Capital and Debenture) Rules 2014.
- Name of the company with Registered office address
- Folio Number
- Share Certificate Number
- Name of Member
- Nature of share number of shares and a distinctive number of shares.
- Amount paid on shares
- Common seal, if any, and signature of two directors and company secretary.
Question 6.
What are the effects of forfeiture of shares?
Answer:
If a shareholder, who is called upon to pay any call fails to pay the amount, even after sending many reminders the company may forfeit his shares. Thus forfeiture of shares means cancellation of shares.
Effects of Forfeiture
- Cessation of Membership: On forfeiture, a member ceases to be a member of a company and loses all membership rights. The member’s name is removed from the Register of Members.
- Liability of Member: A member is liable for unpaid calls even after forfeiture of shares. The liability ceases only when the company reissues the forfeited shares.
- Liquidation of Company: If a company goes in for liquidation within one year of forfeiture of shares, the member whose shares have been forfeited is liable to pay the calls as a past member.

Question 7.
When can the Board of Directors refuse the transfer of shares?
Answer:
- Board of Directors can refuse transfer of shares as they have authority to refuse registration of transfer of shares.
- A notice of refusal of transfer is to be sent by the board to a member within 30 days from the date on which the instrument of transfer is received by the company.
- The board may refuse to register the transfer under following conditions.
- When the provisions for transfer of shares as given in the Articles of Association are not fulfilled by the member.
- When the instrument of transfer is not as per the rules prescribed under the Companies Act.
- When the instrument is not accompanied by the share certificate.
- When the company has a lien on the shares to be transferred.
Question 8.
Explain Employee Stock Option Scheme.
Answer:
An employee stock option plan is an employee benefits scheme under which the company encourages its employees to acquire ownership in the form of shares. Under this scheme, permanent employees, Directors or Officers of the Company or its holding company or subsidiary company are offered the benefit or right to purchase the equity shares of the company at a future date at a predetermined price. Generally these shares are issued at discount. The shares are offered at a price lesser than their market price.
Following are the provisions related to ESOS:
- A company may offer the shares directly to the employees or through an Employee Welfare Trust.
- The shares are offered at a price lesser than their market price.
- There is a minimum vesting period of one year.
- Company specifies the lock-in period. It is a minimum of one year between grant of option and vesting.
- Shares issued under this scheme enjoys dividend or voting rights only after buying by employees.
- Company has to get the approval of shareholders through a special resolution to issue ESOS.
- Employee neither transfer his option to any other person nor pledge/mortgage the shares issued under ESOS.
- Company has to set up a compensation committee to administer ESOS.
- The company has to fulfil the provision of SEBI (Share Based Employee Benefits) Regulations, 2014.

Question 9.
What are Calls on shares?
Answer:
- Whenever a company issues shares, the company may ask its shareholder to pay value of shares in installment which is known as calls on shares.
- Company can demand part or full amount of balance amount of unpaid shares.
- Beside the application money and allotment money if a company demands the balance unpaid amount on shares it is called as calls on shares.
- The unpaid amount on partly paid-up shares is a liability of the shareholders.
- Calls on shares can be made by the Board of Directors in the interest of the company.
- To make a call on shares, company has to send a call letter or notice to the shareholders. This notice is drafted by a secretary and issued in the name of the board of directors. The company gives them a minimum of 14 days notice to pay calls money to the Company’s Banker.
- No call can be made for more than 25% of the nominal value of shares.
Question 10.
Explain private placement method for the issue of shares.
Answer:
- When a company offers its securities to a select group of persons not exceeding 200, it is called a private placement.
- In private placement, the company offers its securities only to identified person and not to the general public.
- Statement in lieu of prospectus should be filed by the company with ROC before making a private placement.
- The Board of directors selects or identify the persons to be included in the select group. They can be mutual funds, Institutional Investors etc.
- Company has to issue private placement offer letter along with the application.
- The shares offered can be fully or partly paid up and the consideration should be paid by cheque, Demand Draft, etc. but not by cash.
- Right to renunciation is not given to applicants under private placement. The company has to get approval of shareholders through a special resolution.
- A company can make private placement through a rights issue and preferential allotment.
6. Justify the following statements.
Question 1.
Company has to fulfill certain provisions while making Right Issue.
Answer:
- When a company wants to issue further capital it can issue shares to its existing equity shareholders which is called Rights Issue.
- According to the Companies Act 2013 company has to fulfil certain provisions for a making Rights Issue.
- The provisions are
- Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
- A company has to send ‘Letter of offer’ to the existing shareholders at the time of issuing Right Shares.
- The letter of offer shall mention
- The number of shares offered.
- The Period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of offer.
- The letter of offer can be sent by registered post, speed post, courier or through electronic mode.
- If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and company can offer the unsold shares to new Investors.

Question 2.
To issue Bonus shares a company has to fulfil certain provisions.
Answer:
- Bonus shares are fully paid shares issued free of cost to the existing equity shareholders.
- According to Companies Act 2013, every company has to follow certain provisions to issue Bonus Shares.
Following are the provisions related to Bonus Issue-
- A company can issue Bonus shares only out of
- Free reserves or
- Securities Premium Account
- Capital Redemption Reserve Account
- A company cannot issue Bonus Shares only out of Reserves credited by the Revaluation of Assets.
- It also cannot issue Bonus Shares instead of paying dividends.
- Once the announcement for Bonus Shares is made by the Board of Directors, it cannot be then withdrawn.
- Bonus shares are fully paid up shares.
- Shareholders cannot renounce i.e., give away their Bonus Shares to another person.
- There is no minimum subscription to be collected.
Question 3.
ESOS is offered by a company to its permanent employees, Directors, and officers.
Answer:
- A company can raise funds by offering shares to its existing permanent employees by ESOS Scheme.
- Under this scheme permanent employees Directors or officers of the company are offered the benefit or right to purchase the equity shares of the company at a future date with a pre-determined price.
- ESOS is followed by the company to encourage its employees and to give certain benefits to them.
- Through ESOS, the company can retain its good and talented employees.
- A company may offer the shares directly to the employees or through an Employee Welfare Trust.
- It is helpful to the company to generate goodwill in the market also.
Question 4.
The company has to fulfill general principles/rules for allotment of shares.
Answer:
Every company issuing shares has to follow rules or general principles given by the Companies Act, 2013 as follows:
- Proper Authority: The Board of Directors or the allotment committee set up by the Board has the authority to allot shares.
- Allotment must be against application only: A Company can allot shares only if it has received a written application for shares from the applicant. Allotment of shares cannot take place on the basis of an oral request.
- Reasonable time: As per the Act, allotment shall be done within 60 days of receipt of application money. Allotment can be made from the fifth day from the date of issue of prospectus.
- Absolute and Unconditional allotment: Shares should be allotted on the same terms as stated in the prospectus and application form. No change in terms of allotment or new conditions can be added at the time of allotment.
- Communication: Company has to inform the applicant that shares have been allotted to him by sending a letter of allotment or allotment advice. The letter gives details of a number of shares allotted, amount of Allotment Money to be paid etc.
- Allotment should not be in Contravention (Violation) of any other laws: A company cannot allot shares by violating or contradicting any other existing laws e.g., shares cannot be allotted to a minor, of a country where a company operates its business.

Question 5.
A Company can issue a duplicate share certificate.
Answer:
A Company can issue a duplicate share certificate in the following circumstances:
- If original share certificate has been defaced, mutilated or tom and is surrendered to the company.
- If it has been proved by the holder that the original share certificate is lost or destroyed.
- In case of loss of share certificate, the company puts up a notice in the newspaper to announce the loss of the share certificate.
- If the company does not get any response from the public within the specified time, then the company issues a duplicate share certificate.
- Duplicate share certificate should be issued within three months from the date of application.
- Duplicate share certificate should be issued within 3 months from the date of application with bold ‘duplicate share certificate’ marked on it.
Question 6.
Board of directors has the authority to forfeit shares.
Answer:
- Forfeiture of shares is a process where the company forfeits the shares of a member or shareholder who fails to pay a call on shares. The forfeiture of a share is a forceful activity performed by a company due to non-payment of calls by shareholders.
- Only the Board of directors can forfeit the shares if the process of forfeiture is authorised by the Articles of Association.
- Board of directors can forfeit shares only in the interest of the company.
- A 14 days of notice should be sent to a concerned member.
- Thus Board of directors can make forfeiture of shares.
Question 7.
A member of a public company can transfer shares.
Answer:
- Transfer of shares means voluntary transfer of shares by a member of a company to another person against consideration.
- In the case of public companies, shares are freely transferable subject to provisions of the Articles of Association.
- A member has to apply to the company for the transfer of shares by filling the ‘Instrument of Transfer’.
- Member who is transferring the shares is called as Transferor and to whom shares are transferred is called Transferee.
- Transfer is said to be completed only when the transfer is registered in the Register of Members.

Question 8.
The Board of Directors can refuse the transfer of shares.
Answer:
- Board of Directors can refuse transfer of shares as they have authority to refuse registration of transfer of shares.
- A notice of refusal of transfer is to be sent by the board to a member within 30 days from the date on which the instrument of transfer is received by the company.
- The board may refuse to register the transfer under the following conditions.
- When the provisions for transfer of shares as given in the Articles of Association is not fulfilled by the member.
- When the instrument of transfer is not as per the rules prescribed under the Companies Act.
- When the instrument is not accompanied by the share certificate.
- When the company has a lien on the shares to be transferred.
7. Answer the following questions.
Question 1.
Explain the classification of Share Capital.
OR
Explain types of Share Capital.
Answer:
Share capital is the capital that is built up by the company by issuing shares in the market. Share capital consist of capital that is made up of Equity shares and Preference shares.
Share capital can be classified as-
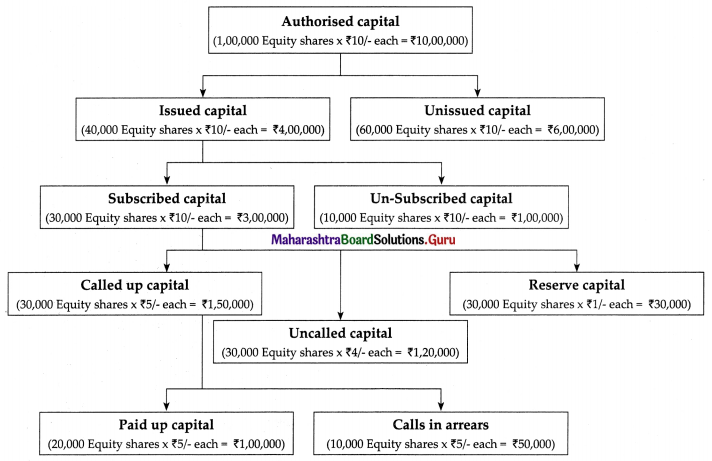
(i) Authorised or Nominal or Registered Capital
- The Authorized capital is the maximum amount of capital that a company can raise through the issue of shares to the shareholders.
- The Authorized capital of a company is also called as the Registered capital or Nominal Capital.
- Authorized capital is the maximum capital that is authorized by the company’s Memorandum of Association.
- The Authorized capital is mentioned in the Memorandum of Association of the company under the heading ‘capital clause’ and the company pays stamp duty on this amount at the time of incorporation.
- Authorized capital is also called as ‘Nominal Capital’ as usually a company never issues the entire Authorized Capital.
- A company can increase its Authorized Capital by altering its Memorandum of Association.
- The maximum limit of authorized capital is registered with the registrar of the companies.
- Example of Authorized Capital: XYZ Ltd. Company has an authorized capital of ₹ 10,00,000, then it can issue shares worth up to ₹ 10,00,000 to its shareholders and cannot issue anything beyond it.
(ii) Issued and Unissued capital:
- Issued capital is that portion of authorized shares capital that had been raised by issuing shares to the general public.
- These are the shares that the company offers to prospective investors for a subscription.
- The issued capital of a company may be equal to or less than the Authorized Capital of incorporation.
- The balance part of Authorized Capital which is not offered to the public for subscription is called ‘unissued capital’.
- Unissued capital is that capital which a Company is authorized to issue but has not issued as shares.
- Unissued capital is the balance part of Authorised capital which is not offered to the public.
- Example of Issued and Unissued Capital: XYZ Ltd Company can have issued Capital of ₹ 4,00,000 divided into 40,000
- Equity Shares at Face Value of ₹ 10/- each and the Unissued Capital 6,00,000 divided into 60,000 equity shares of ₹ 10/- each.

(iii) Subscribed and Unsubscribed Capital:
- Subscribed share capital is that part of issued share capital for which a company has positively received a subscription from the investor.
- It is a part of Issued Capital that has been subscribed by investors or purchased by the general public.
- The subscribed capital may be equal to or less than the issued capital.
- The part of the Issued Capital which is not subscribed by the investors is called as ‘Unsubscribed Capital’.
- Example of Issued and Unissued capital: If XYZ Ltd company has issued capital ₹ 4,00,000 i.e., it has issued 40,000 equity shares of ₹ 10 each and company has received subscription for 30,000 shares i.e., for 30,000 equity shares of ₹ 10/- each then its subscribed capital is ₹ 3,00,000 and unsubscribed capital will be ₹ 1,00,000 divided into 10,000 Equity shares of ₹ 10/- each.
(iv) Called up and Uncalled capital and Reserve capital:
- Called up share capital is that part of share capital that has been called by the company for payment from shareholders.
- The company collects the full value of shares in installments and each installment is called a ‘call’.
- Uncalled Capital is that part of subscribed capital that is not demanded from the shareholders.
- A company can decide to keep aside a part of its uncalled capital to be called up only at the time of winding up of a company to meet its financial requirements. Which is called a Reserve Capital.
Example of call up, uncalled and Reserve Capital.
If XYZ Ltd company is to subscribed capital is ₹ 3,00,000 i.e., 30,000 equity shares of face value of ₹ 10/- each. Out of which company made first call of ₹ 5/- per share, so company called up capital will be ₹ 1,50,000 (30,000 Equity shares × ₹ 5/- each = ₹ 1,50,000)
If the company decides to keep ₹ 1/- per share as capital to be collected at the time of the winding-up, the Reserve Capital will be 30,000 (30,000 equity shares of ₹ 10 each.)
Uncalled Capital will be ₹ 1,20,000 (30,000 equity shares were 4 per share which will be called up in the future.)
(v) Paid-up capital and calls in Arrears:
- Paid-up capital is the amount of money a company has received from shareholders in exchange for shares.
- It is the total amount of money paid up by the shareholders when the company has called up or demanded them to pay.
- The paid-up capital can be equal to or less than the authorized capital.
- Unpaid capital means any uncalled or unpaid share capital. The amount not paid to shareholders is also called as calls in Arrears.
- Every shareholder has to pay calls as and when the company demands, failure to pay the calls may lead to future forfeiture of shares (cancellation of shares).
Example of paid up capital and calls in Arrears.
‘XYZ’ Ltd Company has made a call of ₹ 5/- per share on 30,000 equity shares, so if all the shareholder have paid the calls, then paid-up capital will be ₹ 1,50,000 (30,000 equity shares of ₹ 5/- per share). But if 10,000 Equity Shareholders have not paid calls then the paid-up capital will be ₹ 1,00,000 (20,000 Equity Shares × ₹ 5/- per share) and calls in Arrears will be ₹ 50,000 (10,000 Equity Shares × ₹ 5/- per share).
Question 2.
What are the methods of issue of shares to the public through public offer?
Answer:
Issue of shares is the process in which companies offer new shares to shareholders. The company follows different methods prescribed by the Companies Act 2013 while issuing the shares. There are two methods of issue of shares to the public through public offer, they are – Public issue or Public offer of shares.
A public offering is the sale of equity shares to the public in order to raise capital. This is the most popular and common method used by companies. The company invites the public to subscribe to its shares by issuing prospects. A company can use two pricing methods to offer shares to the public.
(i) Fixed Price Issue method:
- In an initial public offering (IPO), if the shares are offered at a fixed price such issue is known as Fixed Price issue.
- In this method, company mentions the Quantity and the price at which shares are offered.
- Investors can pay a certain portion of face value of shares or the entire issue price along with the application.
- Company issues shares at par. E.g., shares having a face value of ₹ 100 and is issued as ₹ 100, at premium e.g., a share having a face value of 100 and is issued at ₹ 150, or at discount e.g., face value is ₹ 100 and the insured price is ₹ 80/-.
- Fixed price method is used for all types of issues i.e. Public issue, Right issue, Esos etc.

(ii) Book Building Method:
- The method of offering shares by providing a price range is called the book building method.
- In the book building method shares will be sold by the bidding process.
- The company issues a Red Herring Prospectus which contains a price range or price band and asks the investor to bid on it.
- In this method the company doesn’t fix up a particular price for the share but gives a price range e.g., ₹ 80 to 100.
- When bidding for the shares, investors have to decide at which price they would like to bid for the shares e.g., ₹ 80, ₹ 90, ₹ 100.
- The lower price band (₹ 80) is known as the floor price and the highest price band (₹ 100) is known as cap price. The final price at which shares are offered to investors is called cut off price.
- Based on the demand and supply of the shares, the final price is fixed.
- Investors can bid on any number of shares that they are willing to buy at given price band. Such bidding is kept open for 5 days.
- The bids with application money is to be submitted to the Lead Merchant Bankers called ‘Book Runners’ who enter the bids in a book.
- After bidding, the company fixes cut off the price at which shares on offer can be sold.
- Company issues a prospectus which contains the final price.
- Book Building method is used for public issues i.e. IPO and FPO.
Further public offer:
It is also called a follow on public offer. When the company issue shares to the public after IPO, it is called a a further public offer. Thus every issue of shares by a listed company after its IPO is called as FPO. FPO leads to an increase in the subscribed capital of the company.
Question 3.
Explain briefly the different types of shares offered by a company to its existing equity shareholders.
Answer:
The company issues equity shares in the market. The equity shareholders are the real owner of the company.
A company can raise funds by offering shares to its existing equity shareholders as follows.

(i) Right Issue:
A right issue is an invitation to existing shareholders to purchase additional new shares in the company. A right issue is a way by which a listed company can raise additional capital. Instead of going for the public issue of shares, the company gives its existing shareholders, the right to subscribe to newly issued shares in proportion to their existing equity shareholding.
Whenever a company makes the further issue of shares the existing equity shareholders have preemptive rights means the first option to buy shares.
Company making rights issue has to fulfil the following provision:
- Rights shares are sold to the existing shareholders at a price that is lesser than its market price.
- A company has to send a ‘Letter of offer’ to the existing shareholders at the time of issuing Rights Shares.
- The letter of offer shall mention
- The number of shares offered.
- The period of offer i.e., offer is valid for a period not less than fifteen days and not exceeding thirty days from the date of the offer.
- The letter of offer can be sent by registered post, speed post, courier or through electronic mode.
- If a shareholder does not respond to the Rights Issue offer within a given time, it is implied that he is not interested in the offer and company can offer the unsold shares to new Investors.
(ii) Bonus Issue/Bonus Shares:
Bonus Shares are shares distributed by a company to its current shareholders as fully paid shares free of charge. The Bonus shares are given to the existing equity shareholders according to their existing proportion of equity shareholdings.
Like for example, a company declaring one for two bonus share proportion means that an existing shareholder would get one bonus share of the company for every two shares held. Financially sound companies issue Bonus shares out of their accumulated distributable profits or reserves. Hence as the profits or reserves are capitalized, it is called “Capitalisation of Profits or Reserves.”

Following are the provisions related to Bonus Issue-
- A company can issue Bonus shares only out of
- Free reserves or
- Securities Premium Account
- Capital Redemption Reserve Account
- A company cannot issue bonus shares only out of Reserves Credited by the Revaluation of Assets.
- It also cannot issue Bonus Shares instead of paying dividends.
- Once the announcement for Bonus shares is made by the Board of Directors, it cannot be then withdrawn.
- Bonus shares are fully paid up shares.
- Shareholders cannot renounce i.e, give away their Bonus Shares to another person.
- There is no minimum subscription to be collected.
Question 4.
Explain the statutory provisions for the allotment of shares.
Answer:
- The allotment of shares is the issuing of new shares to an applicant based on the application submitted or to the existing shareholders.
- Every company has to fulfill the provisions of the Companies Act for making allotment of shares.
- The provisions which are laid down by the Companies Act, 2013 are called statutory provisions.
(i) Registration of Prospectus:
- A copy of the prospectus must be filed with the Registrar of Companies for registration on or before the date of its publication.
- In the case of the newly formed company, a prospectus must be signed by every proposed director or director or his duly authorized advocate. The copy of the prospectus is drafted by the secretary of the company with the permission of the board of directors.
(ii) Application Money:
- The applicant has to pay a minimum of 5% of nominal amount of the shares along with the application form.
- For public limited companies SEBI has specified that application money should be minimum of 25% of the nominal amount of shares.
- The application money is to be paid in the Bank specified by the company.
(iii) Minimum Subscription:
- Minimum Subscription is the amount which is mentioned in the prospectus. It is the minimum amount of shares which should be bought by the subscribers.
- According to SEBI minimum subscription should be 90% of the issue.
- In case the minimum subscription is not collected within the specified time, the company has to return the entire amount of application money to the subscribers.
(iv) Closing of Subscription list:
- According to SEBI a company has to keep open its subscription list for at least three working days and not more than ten working days.
- Applicants can apply for shares only when the subscription list is open.
(v) Basic of allotment:
- Allotment of shares will be decided on the basis of each category of subscribers.
- Allotment of shares will be as per the minimum application size which is fixed by the company.

(vi) Over Subscription:
- Oversubscription refers to a situation in which a company receives more application of shares than the number of shares offered.
- SEBI does not allow any allotment which is in excess of the offer given by the company through a document or prospectus.
- SEBI may permit to allot the shares not more than 10% of the net offer.
(vii) Permission to deal on Stock Exchanges:
- Every company, before making a public offer shall apply to one or more recognized Stock Exchanges to take permission for listing its shares with them
- The prospectus must mention the name of the stock exchange in which the company is listed.
- The prospectus should also state the fact that an application for permission to list in that stock exchange has been made by the company.
(viii) Appointment of Managers to the issue and various other agencies.
- The company has to appoint one or more Merchant Bankers to act as managers to the public issue.
- The company has to appoint Registrar to the issue (institutions that keeps the records of the issue), collecting bankers and underwriters to the issue as well as brokers to the issue.
- The company has to also appoint self-certified syndicate banks (banks certified by SEBI which offers ASBA facility to investors), which are certified by SEBI, advertising agents, etc.
Question 5.
Explain briefly the procedure for allotment of shares.
Answer:
Allotment of Shares:
- Allotment means distribution of shares among the applicants. It means giving shares to share applicants or to specific persons with whom the company has entered into contract.
- Allotment of shares is a procedure in which shares are distributed to those applicants who have submitted a written application along with the application money. If company allots shares alter fulfilling all statutory and general provisions of Companies Act, 2013 such allotment is called as “Regular Allotment”.
Procedure for Allotment of Shares
(i) Appointment of Allotment Committee
- When the subscription list is closed the secretary informs the Board of Directors to make preparations for allotment of shares.
- If the issue is par subscribed or under subscribed, the Board can do the allotment of shares.
- In case of over subscription the board has to appoint and Allotment Committee to undertake the work of Allotment.
- The Allotment Committees decides the basis of allotment and submits a report to the Board.
(ii) Hold Board Meeting to Decide Basis of Allotment
- Board meeting is held to approve the allotment formula suggested by the Allotment Committee.
- A representative of SEBI should be present when the allotment committee prepares the allotment formula.
- After approval of the allotment formula, an allotment list is made.
- If the shares are listed, then the company should take the permission of the concerned stock exchange.
- The allotment list contains the names of allotters. Which should be signed by the chairman and secretary.
(iii) Pass Board Resolution for allotment:
- A resolution is passed to allot shares in board meeting.
- Secretary sends ‘Letter of Allotment’ to allotters those applicant whom shares are allotted.
- Secretary has to send a ‘Letter of Regret’ to those applicants to whom no shares have been issued.
- Along with the letter of Regret the application money is also refunded.
- The company that issues shares in electronic form informs respective Depository (NSDL or CDSL) about allotment of shares.
- It also provides details of applicants whom shares are allotted, number of shares allotted, etc.

(iv) Collection of Allotment Money:
- The letter of allotment states the money to be paid by the applicant on the allotment of shares.
- The money has to be paid in the Bank specified by the company within the stipulated time.
- For all public issues and rights issues ASBA is compulsory since January 2016.
(v) Arrangement Relating to Letters of Renunciation:
- An applicant who has been allotted shares can renounce the shares in favor of another person.
- The applicant has to fill up a form for renunciation to the company with the original copy of the letter of allotment.
- After the permission of the board, the secretary enters the detail of the new person in the application and allotment list.
(vi) Arrangement Relating to Splitting of Allotment letters:
- An applicant who has been allotted shares can request for the splitting of allotment shares.
- After getting the approval of the Board for the splitting. Secretary enters the details of the split in the list of split allotment for which secretary has to ensure spilled letter.
(vii) File Return of Allotment:
- Secretary has to file a “Return of Allotment’ with the Registrar of Companies within 30 days of allotment of shares.
- The return of allotment contains details of allotment of shares which includes the names and addresses of allotters, the value of shares allotted amount paid or payable on each share, etc.
(viii) Prepare Register of Members and Issue of Share Certificate
- Secretary has to enter the names of all those applicants who have paid the allotment money in the Register of Members.
- Secretary also has to prepare the share certificates and distributes them to all the members within two months from the date of allotment of shares.
Maharashtra State Board 12th Std Secretarial Practice Textbook Solutions
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()