Maharashtra Board 9th Class Maths Part 1 Practice Set 4.2 Solutions Chapter 4 Ratio and Proportion

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.2 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Using the property \(\frac { a }{ b }\) = \(\frac { ak }{ bk }\), fill in the blanks by substituting proper numbers in the following.

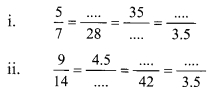
Solution:

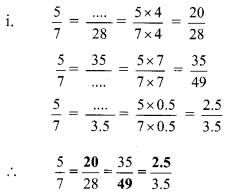
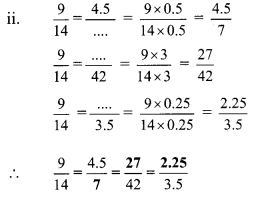
Question 2.
Find the following ratios.
i. The ratio of radius to circumference of the circle.
ii. The ratio of circumference of circle with radius r to its area.
iii. The ratio of diagonal of a square to its side, if the length of side is 7 cm.
iv. The lengths of sides of a rectangle are 5 cm and 3.5 cm. Find the ratio of numbers denoting its perimeter to area.
Solution:
i. Let the radius of circle be r.
then, its circumference = 2πr
Ratio of radius to circumference of the circle

The ratio of radius to circumference of the circle is 1 : 2π.

ii. Let the radius of the circle is r.
∴ circumference = 2πr and area = πr²
Ratio of circumference to the area of circle

∴ The ratio of circumference of circle with radius r to its area is 2 : r.

iii. Length of side of square = 7 cm
∴ Diagonal of square = √2 x side
= √2 x 7
= 7 √2 cm
Ratio of diagonal of a square to its side

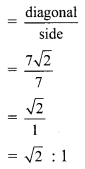
∴ The ratio of diagonal of a square to its side is √2 : 1.

iv. Length of rectangle = (l) = 5 cm,
Breadth of rectangle = (b) = 3.5 cm
Perimeter of the rectangle = 2(l + b)
= 2(5 + 3.5)
= 2 x 8.5
= 17 cm
Area of the rectangle = l x b
= 5 x 3.5
= 17.5 cm²
Ratio of numbers denoting perimeter to the area of rectangle

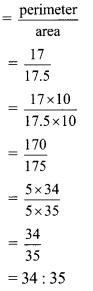
∴ Ratio of numbers denoting perimeter to the area of rectangle is 34 : 35.

Question 3.
Compare the following

Solution:

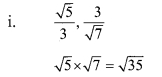
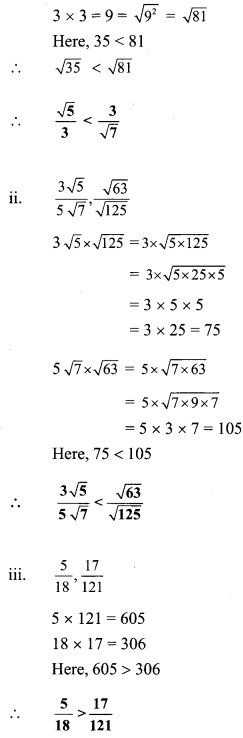
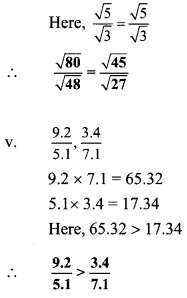
Question 4.
Solve.
ABCD is a parallelogram. The ratio of ∠A and ∠B of this parallelogram is 5 : 4. FInd the measure of ∠B. [2 Marksl
Solution:
Ratio of ∠A and ∠B for given parallelogram is 5 : 4
Let the common multiple be x.

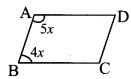
m∠A = 5x°and m∠B=4x°
Now, m∠A + m∠B = 180° …[Adjacent angles of a parallelogram arc supplementary]
∴ 5x° + 4x°= 180°
∴ 9x° = 180°
∴ x° = 20°
∴ m∠B=4x°= 4 x 20° = 80°
∴ The measure of ∠B is 800.

ii. The ratio of present ages of Albert and Salim is 5 : 9. Five years hence ratio of their ages will be 3 : 5. Find their present ages.
Solution:
The ratio of present ages of Albert and Salim is 5 : 9
Let the common multiple be x.
∴ Present age of Albert = 5x years and
Present age of Salim = 9x years
After 5 years,
Albert’s age = (5x + 5) years and
Salim’s age = (9x + 5) years
According to the given condition,
Five years hence ratio of their ages will be 3 : 5
\(\frac{5 x+5}{9 x+5}=\frac{3}{5}\)
∴ 5(5x + 5) = 3(9x + 5)
∴ 25x + 25 = 27x + 15
∴ 25 – 15 = 27 x – 25 x
∴ 10 = 2x
∴ x = 5
∴ Present age of Albert = 5x = 5 x 5 = 25 years
Present age of Salim = 9x = 9 x 5 = 45 years
∴ The present ages of Albert and Salim are 25 years and 45 years respectively.

iii. The ratio of length and breadth of a rectangle is 3 : 1, and its perimeter is 36 cm. Find the length and breadth of the rectangle.
Solution:
The ratio of length and breadth of a rectangle is 3 : 1
Let the common multiple be x.
Length of the rectangle (l) = 3x cm
and Breadth of the rectangle (b) = x cm
Given, perimeter of the rectangle = 36 cm
Since, Perimeter of the rectangle = 2(l + b)
∴ 36 = 2(3x + x)
∴ 36 = 2(4x)
∴ 36 = 8x
∴ \(x=\frac{36}{8}=\frac{9}{2}=4.5\)
Length of the rectangle = 3x = 3 x 4.5 = 13.5 cm
∴ The length of the rectangle is 13.5 cm and its breadth is 4.5 cm.

iv. The ratio of two numbers is 31 : 23 and their sum is 216. Find these numbers.
Solution:
The ratio of two numbers is 31 : 23
Let the common multiple be x.
∴ First number = 31x and
Second number = 23x
According to the given condition,
Sum of the numbers is 216
∴ 31x + 23x = 216
∴ 54x = 216
∴ x = 4
∴ First number = 31x = 31 x 4 = 124
Second number = 23x = 23 x 4 = 92
∴ The two numbers are 124 and 92.

v. If the product of two numbers is 360 and their ratio is 10 : 9, then find the numbers.
Solution:
Ratio of two numbers is 10 : 9
Let the common multiple be x.
∴ First number = 10x and
Second number = 9x
According to the given condition,
Product of two numbers is 360
∴ (10x) (9x) = 360
∴ 90x² = 360
∴ x² = 4
∴ x = 2 …. [Taking positive square root on both sides]
∴ First number = 10x = 10x² = 20
Second number = 9x = 9x² = 18
∴ The two numbers are 20 and 18.

Question 5.
If a : b = 3 : 1 and b : c = 5 : 1, then find the value of [3 Marks each]

Solution:
Given, a : b = 3 : 1
∴ \(\frac { a }{ b }\) = \(\frac { 3 }{ 1 }\)
∴ a = 3b ….(i)
and b : c = 5 : 1
∴ \(\frac { b }{ c }\) = \(\frac { 5 }{ 1 }\)
b = 5c …..(ii)
Substituting (ii) in (i),
we get a = 3(5c)
∴ a = 15c …(iii)

Ratio and Proportion 9th Class Practice Set 4.1 Question 6. If \(\sqrt{0.04 \times 0.4 \times a}=0.4 \times 0.04 \times \sqrt{b}\) , then find the ratio \(\frac { a }{ b }\).
Solution:
\(\sqrt{0.04 \times 0.4 \times a}=0.4 \times 0.04 \times \sqrt{b}\) … [Given]
∴ 0.04 x 0.4 x a = (0.4)² x (0.04)² x b … [Squaring both sides]

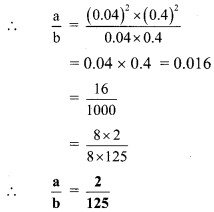
9th Algebra Practice Set 4.2 Question 7. (x + 3) : (x + 11) = (x – 2) : (x + 1), then find the value of x.
Solution:
(x + 3) : (x + 11) = (x- 2) : (x+ 1)
\(\quad \frac{x+3}{x+11}=\frac{x-2}{x+1}\)
∴ (x + 3)(x +1) = (x – 2)(x + 11)
∴ x(x +1) + 3(x + 1) = x(x + 11) – 2(x + 11)
∴ x² + x + 3x + 3 = x² + 1 lx – 2x – 22
∴ x² + 4x + 3 = x² + 9x – 22
∴ 4x + 3 = 9x – 22
∴ 3 + 22 = 9x – 4x
∴ 25 = 5x
∴ x = 5