Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.1 Questions and Answers.
11th Maths Part 2 Complex Numbers Exercise 1.1 Questions And Answers Maharashtra Board
Question 1.
Simplify:
(i) √-16 + 3√-25 + √-36 – √-625
Solution:
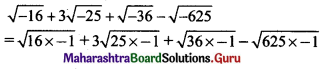
= 4i + 3(5i) + 6i – 25i
= 25i – 25i
= 0
(ii) 4√-4 + 5√-9 – 3√-16
Solution:

Question 2.
Write the conjugates of the following complex numbers
(i) 3 + i
Solution:
Conjugate of (3 + i) is (3 – i).
(ii) 3 – i
Solution:
Conjugate of (3 – i) is (3 + i).
(iii) √-5 – √7 i
Solution:
Conjugate of (√-5 – √7 i) is (√-5 + √7 i).
(iv) -√-5
Solution:
-√-5 = -√5 × √-1 = -√5 i
Conjugate of (-√-5) is √5 i
![]()
(v) 5i
Solution:
Conjugate of (5i) is (-5i).
(vi) √5 – i
Solution:
Conjugate of (√5 – i) is (√5 + i).
(vii) √2 + √3 i
Solution:
Conjugate of (√2 + √3 i) is (√2 – √3 i)
(viii) cos θ + i sin θ
Solution:
Conjugate of (cos θ + i sin θ) is (cos θ – i sin θ)
Question 3.
Find a and b if
(i) a + 2b + 2ai = 4 + 6i
Solution:
a + 2b + 2ai = 4 + 6i
Equating real and imaginary parts, we get
a + 2b = 4 …..(i)
2a = 6 ……(ii)
∴ a = 3
Substituting, a = 3 in (i), we get
3 + 2b = 4
∴ b = \(\frac{1}{2}\)
∴ a = 3 and b = \(\frac{1}{2}\)
Check:
For a = 3 and b = \(\frac{1}{2}\)
Consider, L.H.S. = a + 2b + 2ai
= 3 + 2(\(\frac{1}{2}\)) + 2(3)i
= 4 + 6i
= R.H.S.
(ii) (a – b) + (a + b)i = a + 5i
Solution:
(a – b) + (a + b)i = a + 5i
Equating real and imaginary parts, we get
a – b = a ……(i)
a + b = 5 ……(ii)
From (i), b = 0
Substituting b = 0 in (ii), we get
a + 0 = 5
∴ a = 5
∴ a = 5 and b = 0
![]()
(iii) (a + b) (2 + i) = b + 1 + (10 + 2a)i
Solution:
(a + b) (2 + i) = b + 1 + (10 + 2a)i
2(a + b) + (a + b)i = (b + 1) + (10 + 2a)i
Equating real and imaginary parts, we get
2(a + b) = b + 1
∴ 2a + b = 1 ……(i)
and a + b = 10 + 2a
-a + b = 10 …….(ii)
Subtracting equation (ii) from (i), we get
3a = -9
∴ a = -3
Substituting a = – 3 in (ii), we get
-(-3) + b = 10
∴ b = 7
∴ a = -3 and b = 7
(iv) abi = 3a – b + 12i
Solution:
abi = 3a – b + 12i
∴ 0 + abi = (3a – b) + 12i
Equating real and imaginary parts, we get
3a – b = 0
∴ 3a = b …..(i)
and ab = 12
∴ b = \(\frac{12}{a}\) ……..(ii)
Substituting b = \(\frac{12}{a}\) in (i), we get
3a = \(\frac{12}{a}\)
3a2 = 12
a2 = 4
a = ±2
When a = 2, b = \(\frac{12}{a}\) = \(\frac{12}{2}\) = 6
When a = -2, b = \(\frac{12}{a}\) = \(\frac{12}{-2}\) = -6
∴ a = 2 and b = 6 or a = -2 and b = -6
(v) \(\frac{1}{a+i b}\) = 3 – 2i
Solution:

(vi) (a + ib) (1 + i) = 2 + i
Solution:
(a + ib)(1 + i) = 2 + i
a + ai + bi + bi2 = 2 + i
a + (a + b)i + b(-1) = 2 + i ……(∵ i2 = -1)
(a – b) + (a + b)i = 2 + i
Equating real and imaginary parts, we get
a – b = 2 ……(i)
a + b = 1 …….(ii)
Adding equations (i) and (ii), we get
2a = 3
∴ a = \(\frac{3}{2}\)
Substituting a = \(\frac{3}{2}\) in (ii), we get
\(\frac{3}{2}\) + b = 1
∴ b = 1 – \(\frac{3}{2}\) = \(\frac{-1}{2}\)
∴ a = \(\frac{3}{2}\) and b = \(\frac{-1}{2}\)
Question 4.
Express the following in the form of a + ib, a, b ∈ R, i = √-1. State the values of a and b:
(i) (1 + 2i)(-2 + i)
Solution:
(1 + 2i)(-2 + i) = -2 + i – 4i + 2i2
= -2 – 3i + 2(-1) ……[∵ i2 = -1]
∴ (1 + 2i)(-2 + i) = -4 – 3i
∴ a = -4 and b = -3
![]()
(ii) (1 + i)(1 – i)-1
Solution:

(iii) \(\frac{i(4+3 i)}{1-i}\)
Solution:

(iv) \(\frac{(2+i)}{(3-i)(1+2 i)}\)
Solution:

(v) \(\left(\frac{1+i}{1-1}\right)^{2}\)
Solution:
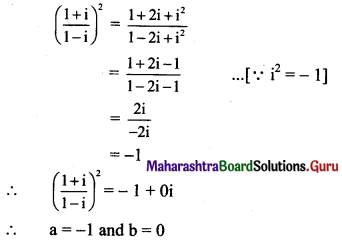
(vi) \(\frac{3+2 i}{2-5 i}+\frac{3-2 i}{2+5 i}\)
Solution:

(vii) (1 + i)-3
Solution:

(viii) \(\frac{2+\sqrt{-3}}{4+\sqrt{-3}}\)
Solution:

(ix) (-√5 + 2√-4 ) + (1 – √-9 ) + (2 + 3i)(2 – 3i)
Solution:
(-√5 + 2√-4) + (1 – √-9) + (2 + 3i)(2 – 3i)
= (-√5 + 2√4.√-1) + (1 – √9.√-1) + 4 – 9i2
= [-√5 + 2(2)i] + (1 – 3i) + 4 – 9i2
= -√5 + 4i + 1 – 3i + 4 – 9(-1) ……[∵ i2 = -1]
= (14 – √5) + i
∴ a = 14 – √5 and b = 1
![]()
(x) (2 + 3i)(2 – 3i)
Solution:
(2 + 3i)(2 – 3i)
= 4 – 9i2
= 4 – 9(-1) …[∵ i2 = -1]
= 4 + 9
= 13
∴ (2 + 3i)(2 – 3i) = 13 + 0i
∴ a = 13 and b = 0
(xi) \(\frac{4 i^{8}-3 i^{9}+3}{3 i^{11}-4 i^{10}-2}\)
Solution:

Question 5.
Show that (-1 + √3i)3 is a real number.
Solution:

Question 6.
Find the value of (3 + \(\frac{2}{\mathrm{i}}\)) (i6 – i7) (1 + i11).
Solution:

Question 7.
Evaluate the following:
(i) i35
(ii) i888
(iii) i93
(iv) i116
(v) i403
(vi) \(\frac{1}{i^{58}}\)
(vii) i-888
(viii) i30 + i40 + i50 + i60
Solution:

Question 8.
Show that 1 + i10 + i20 + i30 is a real number.
Solution:

= 1 – 1 + 1 – 1
= 0, which is a real number.
Question 9.
Find the value of
(i) i49 + i68 + i89 + i110
(ii) i + i2 + i3 + i4
Solution:

![]()
Question 10.
Simplify: \(\frac{\mathbf{i}^{592}+\mathbf{i}^{590}+\mathbf{i}^{588}+\mathbf{i}^{586}+\mathbf{i}^{584}}{\mathbf{i}^{582}+\mathbf{i}^{580}+\mathbf{i}^{578}+\mathbf{i}^{576}+\mathbf{i}^{574}}\)
Solution:

Question 11.
Find the value of 1 + i2 + i4 + i6 + i8 + …… + i20.
Solution:

Question 12.
Show that 1 + i10 + i100 – i1000 = 0.
Solution:

Question 13.
Is (1 + i14 + i18 + i22) a real number? Justify your answer.
Solution:

Question 14.
Evaluate: \(\left(\mathbf{i}^{37}+\frac{1}{\mathbf{i}^{67}}\right)\)
Solution:

Question 15.
Prove that: (1 + i)4 × \(\left(1+\frac{1}{\mathrm{i}}\right)^{4}\) = 16
Solution:

Question 16.
Find the value of \(\frac{\mathbf{i}^{6}+\mathbf{i}^{7}+\mathbf{i}^{8}+\mathbf{i}^{9}}{\mathbf{i}^{2}+\mathbf{i}^{3}}\)
Solution:

![]()
Question 17.
If a = \(\frac{-1+\sqrt{3} i}{2}\), b = \(\frac{-1-\sqrt{3} i}{2}\), then show that a2 = b and b2 = a.
Solution:

Question 18.
If x + iy = (a + ib)3, show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a2 – b2)
Solution:
x + iy = (a + ib)3
x + iy = a3 + 3a2bi + 3ab2i2 + b3i3
x + iy = a3 + 3a2bi – 3ab2 – b3i ……[∵ i2 = -1, i3 = -i]
x + iy = (a3 – 3ab2) + (3a2b – b3)i
Equating real and imaginary parts, we get
x = a3 – 3ab2 and y = 3a2b – b3
\(\frac{x}{a}\) = a2 – 3b2 and \(\frac{y}{b}\) = 3a2 – b2
\(\frac{x}{a}+\frac{y}{b}\) = a2 – 3b + 3a2 – b2
\(\frac{x}{a}+\frac{y}{b}\) = 4a2 – 4b2
\(\frac{x}{a}+\frac{y}{b}\) = 4(a2 – b2)
Alternate Method:
x + iy = (a + ib)3
x + iy = a3 + 3a2bi + 3ab2i2 + b3i3
x + iy = a3 + 3a2bi – 3ab2 – b3i …..[∵ i2 = -1, i3 = -i]
x + iy = (a3 – 3ab2) + (3a2b – b3)i
Equating real and imaginary parts, we get
x = a3 – 3ab2 and y = 3a2b – b3
Consider

Question 19.
If \(\frac{a+3 i}{2+i b}\) = 1 – i, show that (5a – 7b) = 0.
Solution:
\(\frac{a+3 i}{2+i b}\) = 1 – i
a + 3i = (1 – i)(2 + ib)
= 2 + bi – 2i – bi2
= 2 + (b – 2)i – b(-1) ……[∵ i2 = -1]
a + 3i = (2 + b) + (b – 2)i
Equating real and imaginary parts, we get
a = 2 + b and 3 = b – 2
a = 2 + b and b = 5
a = 2 + 5 = 7
5a – 7b = 5(7) – 7(5) = 35 – 35 = 0
![]()
Question 20.
If x + iy = \(\sqrt{\frac{a+i b}{c+i d}}\), prove that \(\left(x^{2}+y^{2}\right)^{2}=\frac{a^{2}+b^{2}}{c^{2}+d^{2}}\)
Solution:


Question 21.
If (a + ib) = \(\frac{1+i}{1-i}\), then prove that a2 + b2 = 1.
Solution:
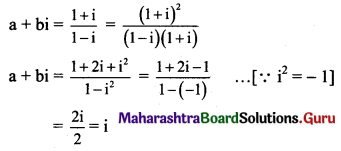
∴ a + bi = 0 + i
Equating real and imaginary parts, we get
a = 0 and b = 1
a2 + b2 = 02 + 12 = 1
Question 22.
Show that \(\left(\frac{\sqrt{7}+i \sqrt{3}}{\sqrt{7}-i \sqrt{3}}+\frac{\sqrt{7}-i \sqrt{3}}{\sqrt{7}+i \sqrt{3}}\right)\) is real.
Solution:

Question 23.
If (x + iy)3 = y + vi, then show that \(\frac{y}{x}+\frac{v}{y}\) = 4(x2 – y2).
Solution:
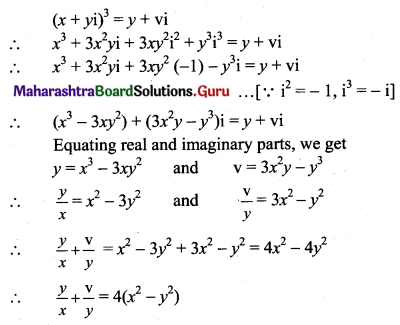
![]()
Question 24.
Find the values of x and y which satisfy the following equations (x, y ∈ R)
(i) (x + 2y) + (2x – 3y)i + 4i = 5
Solution:
(x + 2y) + (2x – 3y)i + 4i = 5
(x + 2y) + (2x – 3y)i = 5 – 4i
Equating real and imaginary parts, we get
x + 2y = 5 ……(i)
and 2x – 3y = -4 …..(ii)
Equation (i) x 2 – equation (ii) gives
7y = 14
∴ y = 2
Substituting y = 2 in (i), we get
x + 2(2) = 5
x + 4 = 5
∴ x = 1
∴ x = 1 and y = 2
Check:
For x = 1 and y = 2
Consider, L.H.S. = (x + 2y) + (2x – 3y)i + 4i
= (1 + 4) + (2 – 6)i + 4i
= 5 – 4i + 4i
= 5
= R.H.S.
(ii) \(\frac{x+1}{1+i}+\frac{y-1}{1-i}=i\)
Solution:

(x + y) + (y – x – 2)i = 2i
(x + y) + (y – x – 2)i = 0 + 2i
Equating real and imaginary parts, we get
x + y = 0 and y – x – 2 = 2
∴ x + y = 0 …….(i)
and -x + y = 4 …….(ii)
Adding (i) and (ii), we get
2y = 4
∴ y = 2
Substituting y = 2 in (i), we get
x + 2 = 0
∴ x = -2
∴ x = -2 and y = 2
(iii) \(\frac{x+i y}{2+3 i}+\frac{2+i}{2-3 i}=\frac{9}{13}(1+i)\)
Solution:

(2x + 3y + 1) + (8 – 3x + 2y)i = 9 + 9i
Equating real and imaginary parts, we get
2x + 3y + 1 = 9 and 8 – 3x + 2y = 9
2x + 3y = 8 ……(i)
and 3x – 2y = – 1 ……(ii)
Equation (i) × 2 + equation (ii) × 3 gives
13x = 13
∴ x = 1
Substituting x = 1 in (i), we get
2(1) + 3y = 8
3y = 6
∴ y = 2
∴ x = 1 and y = 2
![]()
(iv) If x(1 + 3i) + y(2 – i) – 5 + i3 = 0, find x + y
Solution:
x(1 + 3i) + y(2 – i) – 5 + i3 = 0
x + 3xi + 2y – yi – 5 – i = 0 ……[∵ i3 = -i]
(x + 2y – 5) + (3x – y – 1)i = 0 + 0i
Equating real and imaginary parts, we get
x + 2y – 5 = 0 …..(i)
and 3x – y – 1 = 0 ……(ii)
Equation (i) + equation (ii) × 2 gives
7x – 7 = 0
7x = 1
∴ x = 1
Substituting x = 1 in (i), we get
1 + 2y – 5 = 0
2y = 4
y = 2
∴ x = 1 and y = 2
∴ x + y = 1 + 2 = 3
(v) If x + 2i + 15i6y = 7x + i3(y + 4), find x + y
Solution:
x + 2i + 15i6y = 7x + i3(y + 4)
x + 2i + 15(i2)3 y = 7x + i3(y + 4)
x + 2i + 15(-1)3 y = 7x – i(y + 4) ……[∵ i2 = -1, i3 = -i]
x + 2i – 15y – 7x + iy + 4i = 0
(-6x – 15y) + i(y + 6) = 0 + 0i
Equating real and imaginary parts, we get
-6x – 15y = 0 and y + 6 = 0
-6x – 15y = 0 and y = -6
-6x – 15(-6) = 0
-6x + 90 = 0
∴ x = 15
∴ x + y = 15 – 6 = 9
Class 11 Maharashtra State Board Maths Solution