Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 6 Superposition of Waves Important Questions and Answers.
Maharashtra State Board 12th Physics Important Questions Chapter 6 Superposition of Waves
Question 1.
What is a progressive wave?
Answer:
A progressive wave or wave motion is a periodic or oscillatory disturbance in a medium or in a vacuum that is propagated without any damping and obstruction from one place to another at a finite speed.
[Note: A progressive wave is also called a traveling wave.]
Question 2.
Define :
- transverse
- longitudinal progressive wave.
Answer:
- A progressive wave in which the vibration of the individual particles of the medium is perpendicular to the direction of propagation of the wave is called a transverse progressive wave.
- A progressive wave in which the vibration of the individual particles of the medium is along the line of propagation of the wave is called a longitudinal progressive wave.
Question 3.
What is a mechanical wave? Explain.
Answer:
A mechanical wave is a wave motion in a material medium.
Such a wave originates in the displacement of some portion of an elastic medium from its normal position. This causes the layers of matter to oscillate about their equilibrium positions. Because of the elastic properties of the material, the disturbance is transmitted from one layer to the next and so the waveform progresses through the medium.
![]()
Question 4.
What is a simple harmonic progressive wave?
Answer:
A simple harmonic progressive wave is a periodic disturbance in a medium or in a vacuum which propagates at a finite speed and in which the vibrations of the particles of the medium, as in a mechanical wave, or the oscillations of the electric and magnetic fields as in an electromagnetic wave are simple harmonic.
Question 5.
Define the following physical quantities related to a progressive wave :
(1) wave speed
(2) frequency (n)
(3) wavelength
(4) amplitude
(5) period
(6) wave number.
Answer:
(1) Wave speed: The distance covered by a progressive wave per unit time is called wave speed.
(2) Frequency: The number of waves that pass per unit time across a given point of the medium is called the frequency of the wave.
[Note : It is equal to the number of vibrations per unit time made by a particle of the medium.]
(3) Wavelength: Wavelength is the distance between consecutive particles of the medium which are moving in exactly the same way at the same time and have the same displacement from their equilibrium positions.
[Note : Such particles are said to be in the same phase (the same state of vibration).]
(4) Amplitude : The magnitude of the maximum displacement of a particle of the medium from its equilibrium position is called the amplitude of the wave.
(5) Period : The time taken for a complete wave (one wavelength long) to pass a given point in the medium is called the period of the wave.
[Note : It is equal to the periodic time of the vibrational motion of a particle of the medium.]
(6) Wave number : The number of waves present per unit distance is called the wave number.
Question 6.
Write the equation of a progressive wave travelling along the positive x-direction.
Answer:
A progressive wave travelling along the positive x-direction is given by
y(x, t) = A sin (kx – ωt)
where A is the amplitude of the wave, k is the wave number and co is the angular frequency.
[Note : y(x, t) = A sin (kx – ωt), y(x, t) = A sin (ωt – kx), y(x, t) = A cos (kx – ωt), y(x, t) = A cos (ωt – kx) also represent a progressive wave travelling in the positive x-direction. Hence, any one of them can be used. y(x, t) can be written simply as y.]
Question 7.
Write the equation of a progressive wave travelling along the negative x-direction.
Answer:
A progressive wave travelling along the negative x-direction is given by y(x, t) = A sin (kx + ωt)
where A is the amplitude of the wave, k is the wave number and ω is the angular frequency.
![]()
Question 8.
Express the equation of a simple harmonic progressive wave in different forms.
Answer:
A simple progressive wave travelling along the positive x-direction is given by y = A sin (ωt – kx) … (1)
where A is the amplitude of the wave, k is the wave number and co is the angular frequency.

Frequency of vibrations, n = \(\frac{1}{T}\), Eq. (2) can be written as
y = A sin 2π(\(\overline{\mathrm{T}}\) – \(\frac{x}{\lambda}\))
Equations (1), (2), (3), (4), (5) and (6) are the different forms of the equation of a simple harmonic progressive wave.
Question 9.
A simple harmonic progressive wave is given by y = A sin (ωt – kx), where the symbols have their usual meaning. What is
- the particle velocity at a point x and time t
- the wave speed ?
Answer:
- Particle velocity, \(\frac{d y}{d t}\) = ωA cos (ωt – kx)
- Wave speed, v = \(\frac{\omega}{k}\).
Question 10.
A simple harmonic progressive wave has frequency 25 Hz and wavelength 4 m. If the phase difference between motions of two particles is (π/10) rad, what is the corresponding path difference?
Answer:
Path difference = \(\frac{\lambda}{2 \pi}\) × phase difference
= \(\frac{4 \mathrm{~m}}{2 \pi \mathrm{rad}}\) × \(\frac{\pi}{10}\) rad = 0.2 m
Question 11.
A simple harmonic progressive of frequency 100 Hz and wavelength 0.5 m travels through a medium. If the path difference between two points in the path of the wave is 0.1 m, what is the corresponding phase difference ?
Answer:
Phase difference = \(\frac{2 \pi}{\lambda}\) × path difference
= \(\frac{2 \pi}{0.5 \mathrm{~m}}\) × 0.1 m = 0.4 rad
Question 12.
The displacement of a particle of a medium when sound wave propagates is represented by y = A cos (ax + bt) where A, a and b are positive constants. The wave is reflected by an obstacle situated at x = 0.
- What is the wavelength and frequency of the incident wave ?
- Write the equation of the reflected wave.
Answer:
The incident sound wave is represented by y = A cos (ax + bt) where A, a and b are positive constants. The equation of a progressive wave of amplitude A, wavelength λ and frequency n = ω/2π, travelling along the negative direction of the x-axis is
y = A cos (ωt + kx),
where k = 2π/λ is the propagation constant. Comparing the two equations, ω = b and k = a.
- Therefore, the wavelength of the incident wave,
λ = \(\frac{2 \pi}{k}\) = \(\frac{2 \pi}{a}\) and its frequency, n = \(\frac{\omega}{2 \pi}\) = \(\frac{b}{2 \pi}\) - The equation of a progressive wave travelling along the positive direction of the x-axis is
y = A cos (ωt – kx)
∴ The equation of the reflected wave is
y = A cos (bt – ax).
Question 13.
Solve the following :
Question 1.
A simple harmonic progressive wave travels along a string. The time for a particle of the string to move from maximum displacement to zero is 0.004 s. What are the period and frequency of the wave ? If the wavelength is 1.2 m, what is the wave speed?
Solution :
Data : t = 0.004 s, λ = 1.2 m
The period T of the wave = the periodic time of the vibrational motion of the particle of the string = 4t = 4 × 0.004 = 0.016
∴ The frequency of the wave,
n = \(\frac{1}{T}\) = \(\frac{1}{0.016}\) = 62.5 Hz
The wave speed, v = nλ = 1.2 × 62.5 = 75 m/s
![]()
Question 2.
Write the equation of a simple harmonic progressive wave of amplitude 0.05 m and period 0.04 s travelling along the positive x-axis with a velocity of 12.5 m/s.
Solution:
Data : A = 0.05 m, T = 0.04 s, v = 12.5 m/s
∴ Equation of the wave travelling in the positive direction of the x-axis is

Question 3.
A simple harmonic progressive wave is given by the equation y = 0.1 sin 4π (50t – 0.1 x), in SI units. Find the amplitude, frequency, wavelength and speed of the wave.
Solution :
Data : y = 0.1 sin 4π (50t – 0.1 x)
= 0.1 sin 2π (100t – 0.2 x)
= 0.1 sin 2π( 100t – \(\frac{x}{5}\))
Let us compare this equation with that of a simple harmonic progressive wave.
∴ y = A sin 2π(nt – \(\frac{x}{2}\)) = 0.1 sin2π(100t – \(\frac{x}{5}\))
Comparing the quantities on both sides, we get,
- amplitude (A) = 0.1 m
- frequency (n) = 100 Hz
- wavelength (λ) = 5 m
- speed (v) = nλ = 100 × 5 = 500 m/s
Question 4.
The equation of a transverse wave on a stretched string is y = 0.2 sin 2π(\(\frac{t}{0.02}\) – \(\frac{x}{20}\)) where distances are in metre and time in second.
Find the
- amplitude
- frequency
- speed of the wave.
Solution:
Let us compare the given equation with the equation of a simple harmonic progressive wave :
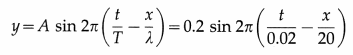
Comparing the quantities on both sides, we get,
A = 0.2 m, T = 0.02 s, λ = 20 m
∴
- Amplitude (A) = 0.2 m
- Frequency (n) = \(\frac{1}{T}\) = \(\frac{1}{0.02}\) = 50 Hz
- Speed (v) = nλ – 50 × 20 = 1000 m/s
Question 5.
The equation of a simple harmonic progressive wave is y = 0.4 sin 100π (t – \(\frac{x}{5}\)) where all quantities are in SI units. Calculate the
- wavelength
- speed of the wave.
Solution:
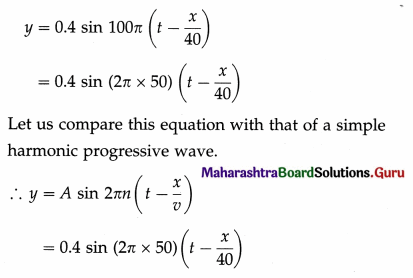
Comparing the quantities on both sides, we get,
A = 0.4 m, n = 50Hz and v = 40m/s
∴
- Speed (v) =40 m/s
- Wavelength (λ) = \(\frac{v}{n}\) = \(\frac{40}{50}\) = 0.8 m
Question 6.
The equation of a simple harmonic progressive wave is given by y = 0.05 sin π (20t – \(\frac{x}{6}\)), where all quantities are in SI units. Calculate the displacement of a particle at 5 m from the origin and at the instant 0.1 second. Also find the phase difference between two particles separated by 5 m.
Solution :
Data : x = 5 m, t = 0.1 s
(i) The displacement of the particle,

Comparing the two sides, we get, λ = 12 m
The phase difference between two points separated by x = 5 m is given by
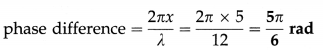
Question 7.
A sound wave of amplitude 0.2 cm, frequency 1000 Hz and wavelength 0.31 m is travelling in air. Calculate the displacement of the particle at 3.1 m from the origin after 1.004 s. What would be the phase difference for two positions of the vibrating particle after an interval of 0.001s?
Solution :
Data : A = 0.2 cm = 0.002 m, n = 1000 Hz, λ = 0.31 m, x = 3.1 m, t = 1.004 s, t2 – t1 = 0.001 s
(i) The displacement of the particle,
y = A sin 2π(nt – \(\frac{x}{\lambda}\))
= 0.002 sin 2π(1000 × 1.004 – \(\frac{3.1}{0.31}\))
= 0.002 sin 2π (1004 – 10)
= 0.002 sin 2π(994) = 0 [or y = 0 metre]
(ii) Phase difference = 2πn (t2 – t1)
= 2π × 1000 × 0.001 = 2π radians
![]()
Question 8.
The equation of a simple harmonic progressive wave is given by y = 4 sin π(\(\frac{t}{0.02}\) – \(\frac{x}{75}\)). Find the displacement and velocity of a particle at 50 cm from the origin and at 0.1 second. (All quantities are expressed in CGS units.)
Solution :

The displacement of the particle, y = 3.464 cm = 3.464 × 10-2 m
The velocity of the particle,

Question 14.
What is meant by reflection of a wave ?
Answer:
When a wave travelling in a medium is incident on a boundary with another medium, a part of it returns into the original medium with a change in its direction of propagation while a part of it is transmitted into the second medium. The phenomenon in which a part of the wave is returned into the original medium with reduction in its intensity and energy is called reflection.
Question 15.
Explain the reflection of transverse waves at the surface of
(1) a denser medium
(2) a rarer medium.
OR
Explain the effect on the phase of transverse waves reflected from
(1) a denser medium
(2) a rarer medium.
Answer:
(1) Reflection of transverse waves from a denser medium : Suppose that a crest of a transverse wave travels along a string and is incident on the surface of a denser medium such as a rigid wall at point B, as shown in below figure. As the crest cannot travel further, it is reflected.
Since point B is fixed, its displacement is always zero. Therefore, the crest must be reflected in such a way, that the displacement at B due to the reflected
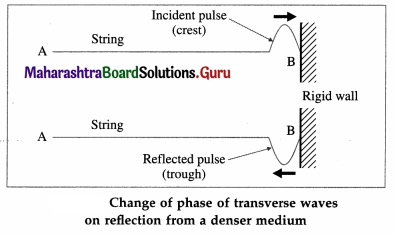
wave is exactly equal in magnitude and opposite in direction to that due to the incident wave. Therefore, the crest is reflected as a trough. Hence, there is a phase change of 180° or π radians when transverse waves are reflected from a denser medium.
(2) Reflection of transverse waves from a rarer medium : In this case, the particles of the medium are free to vibrate. Hence,
- there is no change of phase
- a crest is reflected as a crest and a trough is reflected as a trough.
Question 16.
Consider a heavy string X and a light string Y joined together at point O. Explain what happens when a wave pulse
(1) travelling from the string X reaches the junction O
(2) travelling from the string Y reaches the junction O.
Answer:
The tension in both strings is the same. Hence, the junction O is a discontinuity between string X of greater linear density than string Y because the wave speed is less on X than on Y.
(1) When a pulse travelling on the heavy string X reaches O, the light string Y gets pulled upwards. Thus the pulse, gets partially transmitted and partially reflected as a crest, as shown in below figure. However, the amplitude of transmitted pulse is greater than that of the reflected pulse.
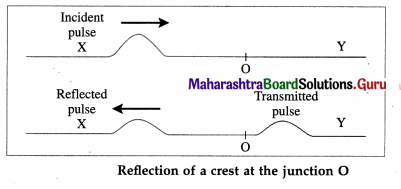
(2) When a pulse travelling on a light string Y reaches O, the heavier string X pulled slightly upwards. Thus, the pulse is partly transmitted as a crest but the reflected part is inverted as a trough, as shown in below figure. Here, the amplitude of transmitted pulse is smaller than that of the reflected pulse.
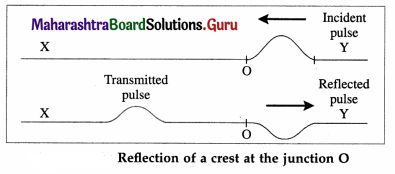
[Note : In either case, the relative heights of the reflected and transmitted pulses depend on the relative densities of the two strings. Obviously, if the strings are identical, there is no discontinuity at the boundary and no reflection takes place.]
Question 17.
A heavy string X is joined to a light string Y at point O. How will a pulse get reflected
(1) travelling on the string X towards O
(2) travelling on the string Y towards O ?
Answer:
(1) A pulse travelling on a heavy string will reflect without inversion at its boundary with a lighter string. Thus, a crest will reflect as a crest and a trough will reflect as a trough.
(2) When a pulse travelling on a light string encounters a boundary with a heavier string, the reflected pulse is inverted. Thus, a crest will reflect as a trough and vice versa.
Question 18.
Explain the reflection of sound waves (i.e., longitudinal waves) at the surface of
(1) a denser medium
(2) a rarer medium.
OR
Explain the effect on the phase of longitudinal waves reflected from
(1) a denser medium
(2) a rarer medium.
Answer:
(1) Reflection of a longitudinal wave from a denser medium : Consider a sound wave incident on a denser medium such as a rigid wall. When a compression is incident on the wall, the particles of air close to the wall are in a compressed state. To return to their normal condition, the particles begin to press in the opposite direction and therefore a compression gets reflected as a compression and a rarefaction is reflected as a rarefaction. However, the displacements of the particles in the reflected wave are opposite to their displacements in the incident wave, so that there is a change of phase of 180° or π radians.
(2) Reflection of a longitudinal wave from a rarer medium : When sound waves are reflected from
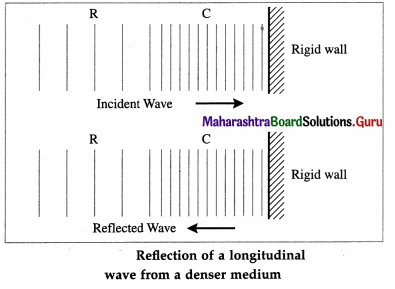
the surface of a rarer medium, there is no change of phase. Therefore, a compression is reflected as a rarefaction and vice versa. The reason is as follows :
When a compression is incident on the surface of a rarer medium, it can pass into that medium. This is because the particles of the rarer medium are free to move and they get compressed, leaving a rarefaction behind, which travels in the opposite direction. In a similar manner an incident rarefaction gets reflected as a compression.
Question 19.
State the principle of superposition of waves.
Answer:
Principle of superposition of waves : The displacement of a particle at a given point in space and time due to the simultaneous influence of two or more waves is the vector sum of the displacements due to each wave acting independently.
Notes :
- The principle of superposition is applicable to all types of waves.
- The phenomena of interference, beats, formation of stationary waves, etc. are based on the principle of superposition of waves.
![]()
Question 20.
Explain the superposition of two wave pulses of equal amplitude and same phase moving towards each other.
OR
Explain constructive interference when two wave pulses of equal amplitude and same phase are superimposed.
Answer:
Consider two wave pulses of the same amplitude and phase moving towards each other, as shown in below figure.
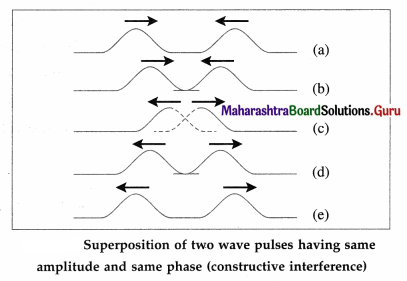
When the two pulses cross each other, stages (b) to (d), the resultant displacement is equal to the vector sum of the displacements due to the individual pulses (shown by dashed lutes). Therefore, the resultant displacement at that point becomes maximum. This phenomenon is called constructive interference. After crossing each other, both the pulses continue to propagate with their initial amplitude.
Question 21.
Explain the superposition of two wave pulses of equal amplitude and opposite phase moving towards each other.
OR
Explain destructive interference when two wave pulses of equal amplitude and opposite phase are superimposed.
Answer:
Consider two wave pulses of the same amplitude but opposite phase moving towards each other, as shown in below figure.
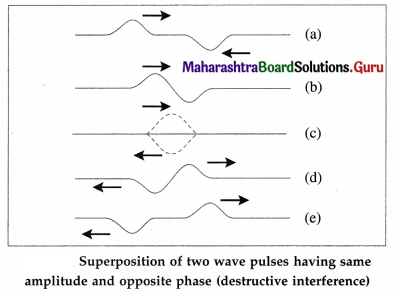
When the two pulses cross each other, stages (b) to (d), the resultant displacement is equal to the vector sum of the displacements due to the individual pulses (shown by dashed lines). Therefore, the resultant displacement at that point becomes minimum, equal to zero, because the individual pulses are exactly 180° out of phase.
[Notes: Music lovers often find many types of ambient sounds that interfere with the sounds coming through their headphones. Active noise-cancelling headphones not only block out some high frequency sound waves but also actively cancel out lower-frequency sound waves by destructive interference. They actually create sound waves with the same amplitude that mimic the incoming noise but with inverted phase (also known as antiphase), i.e., exactly 180° out of phase to the original noise. This inverted signal (in antiphase) is then amplified and a transducer creates a sound wave directly proportional to the amplitude of the original waveform, creating destructive interference. This effectively reduces the volume
of the perceivable noise.]
Question 22.
Derive an equation for the resultant wave produced due to superposition of two waves. Hence, state the expression for the amplitude of the resultant wave when two waves are
(1) in phase
(2) out of phase.
Answer:
Consider two waves of the same frequency, different amplitudes A1 and A2 and differing in phase by φ. Let these two waves interfere at x = 0.
The displacement of each wave at x = 0 are
y1 = A1 sin ωt
y2 = A2 sin (ωt + φ)
According to the principle of superposition of waves, the resultant displacement at that point is
y1 = y1 + y2
= A1 sin ωt + A2 sin (ωt + φ)
Using the trigonometrical identity,
sin (C + D) = sin C cos D + cos C sin D,
y = A1 sin ωt + A2 ωt cos φ + A2 cos ωt sin φ
y = (A1 + A2 cos φ) sin ωt + A2 sin φ cos ωt … (1)
Let (A1 + A2 cos φ) = A cos θ … (2)
and A2 sin φ = A sin θ … (3)
Substituting Eqs. (2) and (3) in EQ. (1), we get the equation of the resultant wave as
y = A cos θ sin ωt + A sin θ cos ωt = A sin (ωt + θ) … (4)
It has the same frequency as that of the interfering waves. The amplitude A of the resultant wave is given by squaring and adding Eqs. (2) and (3).

Thus, the amplitude of the resultant wave is maximum when the two interfering waves are in phase.
Case (2) : When the two interfering waves are out of phase, ivarphi = ipi. Then, the amplitude of the resultant wave is,
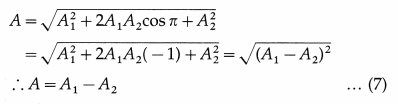
Thus, the amplitude of the resultant wave is minimum when the two interfering waves are in opposite phase.
Question 23.
What is the relation between the amplitude of a wave and its intensity?
Answer:
The intensity of a wave is proportional to the square of its amplitude.
Question 24.
Two interfering waves of the same frequency are out of phase but have different amplitudes A1 and A2. What can you say about the intensity of the resultant wave ?
Answer:
The two interfering waves are out of phase. Thus, the amplitude and hence the intensity of the resultant wave is minimum, Imin ∝ (Amin)2 where (Amin)2 = (A1 – A2)2.
Question 25.
Two interfering waves of the same frequency are in phase but have different amplitudes A1 and A2. What can you say about the intensity of the resultant wave ?
Answer:
The two waves interfere in phase. Thus, the amplitude and hence the intensity of the resultant wave is maximum, Imax ∝ (Amin)2 where (Amax)2 = (A1 + A2)2.
Question 26.
What is a stationary wave? Why is it called stationary?
Answer:
When two progressive waves having the same amplitude, wavelength and speed, travel through the same region of a medium in opposite directions, their super-position under certain conditions creates a stationary interference pattern called as a stationary or standing wave.
It is called stationary because the resultant harmonic disturbance of the particles does not travel in any direction and there is no transport of energy in the medium.
Question 27.
Define :
- transverse stationary wave
- longitudinal stationary wave.
Answer:
- When two identical transverse progressive waves travelling in opposite directions along the same line superimpose, the resultant wave produced is called a transverse stationary wave.
- When two identical longitudinal progressive waves superimpose, the resultant wave produced is called a longitudinal stationary wave.
Question 28.
When stationary waves of wavelength 40 cm are formed in a medium, what is the distance between
- successive nodes
- a node and the next antinode?
Answer:
- 20 cm
- 10 cm.
Question 29.
The equation of a stationary wave is y = 0.04 cos \(\frac{2 \pi x}{0.6}\) sin 2π (100t) with all quantities in SI units. What is the length of one loop ?
Answer:
Comparing the given equation with
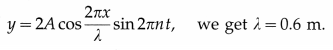
∴ Length of one loop = \(\frac{\lambda}{2}\) = 0.3 m.
Question 30.
What is the speed of the waves superposed ? For data, see Question 29.
Answer:
n = 100 Hz. v = nλ = 100 × 0.6 = 60 m/s.
Question 31.
What is the maximum speed of a particle at an antinode ? For data, see Question 29.
Answer:
vmax = 2A(2πn) = 0.04 × 2π × 100 = 8π m/s.
Question 32.
Distinguish between progressive waves and stationary waves.
Answer:
Progressive and stationary waves :
| Progressive waves | Stationary waves |
| 1. They are produced when a disturbance is created in the medium. | 1. They are produced due to interference, under certain conditions, between two identical progressive waves travelling in opposite directions. |
| 2. They continuously travel away from the source and transport energy through the medium. | 2. They do not move in any direction and hence do not transport energy through the medium. |
| 3. Every particle vibrates with the same amplitude. | 3. Amplitude of vibration is different for different particles |
| 4. Phase changes from particle to particle | 4. All the particles in the same loop have the same phase, while the particles in adjacent loops are in opposite phase. |
| 5. Every particle of the medium is set into vibrations | 5. There are some particles of the medium which do not vibrate at all. |
Question 33.
Solve the following :
Question 1.
A sound wave of frequency 1000 Hz and travelling with speed 340 m/s is reflected from the closed end of the tube. At what distance from that end will the adjacent node occur?
Solution :
Data : n = 1000 Hz, v = 340 m/s
The wavelength of the stationary wave set up in the tube, λ = \(\frac{v}{n}\).
The distance between successive nodes
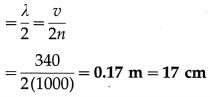
Question 2.
Two simple harmonic progressive waves are represented by y1 = 2 sin 2π(100 t – \(\frac{x}{60}\)) cm and y2 = 2 sin 2π(100t + \(\frac{x}{60}\)) cm. The waves combine to form a stationary wave. Find
- the amplitude at an antinode
- the distance between adjacent node and antinode
- the loop length
- the wave speed.
Solution :
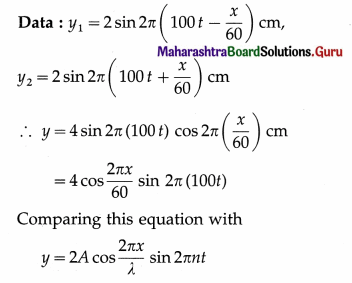
we get, λ = 60 cm and n = 100 Hz. Therefore,
- the amplitude at an antinode, | 2A | = 4 cm
- the distance between adjacent node and antinode \(\frac{\lambda}{4}\) = \(\frac{60}{4}\) = 15 cm
- the loop length = \(\frac{\lambda}{2}\) = \(\frac{60}{2}\) cm = 30 cm
- the wave speed = nλ= 100 × 60 = 6000 cm/s
![]()
Question 3.
The equation of a standing wave is given by y = 0.02 cos (πx) sin (100 πt) m. Find the amplitude of either wave interfering, wavelength, time period, frequency and wave speed of interfering waves.
Solution :
Data : y = 0.02 cos (πx) sin (100 πt) m
Comparing this equation with
y = 2A cos\(\left(\frac{2 \pi x}{\lambda}\right)\) sin (2π nt)
we get for either interfering waves,
- the amplitude, | A | = \(\frac{0.02}{2}\) = 0.01 m
- the wavelength, λ = 2 m
- the time period, T = \(\frac{1}{n}\) = \(\frac{1}{50}\)s = 0.02 s
- the frequency, n = 50 Hz
- the wave speed = nλ = 50 × 2 = 100 m/s
Question 34.
Explain
(1) free vibrations
(2) forced vibrations.
Answer:
(1) Free vibrations : A body capable of vibrations is said to perform free vibrations when it is disturbed from its equilibrium position and left to itself.
In the absence of dissipative forces such as friction due to surrounding air and internal forces, the total energy and hence the amplitude of vibrations of the body remains constant. The frequencies of the free vibrations of a body are called its natural frequencies and depend on the body itself.
In the absence of a maintaining force, in practice, the total energy and hence the amplitude decreases due to dissipative forces and the vibration is said to be damped. The frequency of damped vibrations is less than the natural frequency.
(2) Forced vibrations : The vibrations of a body in response to an external periodic force are called forced vibrations.
The external force supplies the necessary energy to make up for the dissipative losses. The frequency of the forced vibrations is equal to the frequency of the external periodic force.
The amplitude of the forced vibrations depends upon the mass of the vibrating body, the amplitude of the external force, the difference between the natural frequency and the frequency of the periodic force, and the extent of damping.
Question 35.
Define resonance.
Answer:
Resonance : If a body is made to vibrate by an external periodic force, whose frequency is equal to the natural frequency (or nearly so) of the body, the body vibrates with maximum amplitude. This phenomenon is called resonance.
The corresponding frequency is called the resonant frequency.
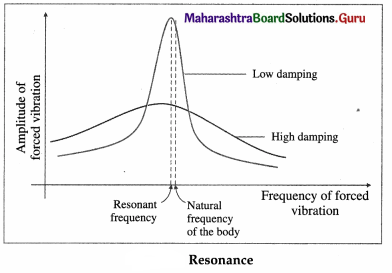
For low damping, the amplitude of vibrations has a sharp maximum at resonance, as shown in above figure. The flatter curve without a pronounced maximum is for high damping.
Question 36.
Distinguish between
(1) free vibrations and resonance
(2) forced vibrations and resonance (Two points of distinction).
Answer:
(1) Free vibrations and resonance:
| Free vibrations | Resonance |
| 1. These are produced when a body is distributed from its equilibrium position and released. | 1. It is produced by forced vibrations when the external periodic force has the frequency equal to the natural frequency (or nearly so) of the body. |
| 2. The energy of the body remains constant in the absence of dissipative forces. | 2. Energy is supplied continuously by the external periodic force to compensate the loss of energy due to the dissipative forces. |
(2) Forced vibrations and resonance :
| Forced vibrations | Resonance |
| 1. These are produced by an external periodic force of any frequency. | 1. It is produced by an external periodic force whose frequency is equal to the natural frequency (or nearly so) of the body. |
| 2. The frequency of vibrations is, in general, different from the natural frequency of the body | 2. The frequency of vibrations is the same (or nearly so) as the natural frequency of the body. |
| 3. The amplitude of vibrations is usually very small. | 3. The amplitude of vibrations is large. |
| 4. Vibrations stop as soon as the external force is removed. | 4. Vibrations continue for relatively longer time after the external force is removed. |
Question 37.
Give any two applications of resonance.
Answer:
- A radio or TV receiver set is tuned to the frequency of the desired broadcast station by adjusting the resonant frequency of its electrical oscillator circuit.
- The speed of sound at room temperature can be determined by making the air column of a resonance tube resonate with a vibrating tuning fork of known frequency.
- The frequency of a tuning fork can be determined by making a sonometer wire, of known mass per unit length and under known tension, resonate with the vibrating fork.
- The amplitude of the oscillations of a child on a swing is increased by pushing with a frequency equal to the natural frequency of the swing.
Question 38.
Give any two disadvantages of resonance.
Answer:
- A column of soldiers marching in regular step on a narrow and structurally flexible bridge can set it into dangerously large amplitude oscillations. The bridge may even collapse at the resonance.
- Structural resonance of a suspension bridge induced by the winds can lead to its catastrophic collapse. Several early suspension bridges were destroyed by structural resonance induced by modest winds.
- Vibrations of a motor or engine can induce resonant vibrations in its supporting structures if their natural frequency is close to that of the vibrations of the engine. A common example is the rattling sound of a bus body when the engine is left idling. Vibrations in an aircraft are caused by the engine and the aerodynamic effects. The vibrations cause metal fatigue, especially in the fuselage, wings and tail, and eventually lead to metal fracture.
- Every ship has a natural period of rolling (side to side oscillation about an axis along its length). If the ship encounters a series of waves such that the wave period matches the rolling, it will have no time righting itself before the next wave strikes. Resonant conditions can occur when the combination of wave period, vessel speed and heading with respect to the waves lead to an encounter close to the natural roll period of the vessel. This situation, if not corrected, can lead to severe rolling, with roll angle exceeding 15°.
Large containerships are particularly vulnerable to rolling. Possible consequences are loss of containers, machinery failure, structural damage and even capsizing of the ship. The speed and direction of the ship can be changed to avoid the consequences of synchronous rolling.
Question 39.
What are overtones? What is the meaning of first overtone ?
Answer:
The higher allowed harmonics above the first harmonic or fundamental are called overtones.
The first overtone is the higher allowed harmonic immediately above the first harmonic.
![]()
Question 40.
Distinguish between harmonics and overtones.
Answer:
| Harmonics |
Overtones |
| 1. The lowest allowed frequency of vibration (fundamental) of a bounded medium and all its integral multiples are called harmonics. | 1. The higher allowed frequencies of vibration above the fundamental are called overtones. |
| 2. The lowest allowed frequency (fundamental), n, is called the first harmonic. The second harmonic is In, third harmonic is 3n, … and so on. | 2. Above the fundamental, the first allowed frequency is called the first overtone which may be either the second or third harmonic. Depending on the system, the pth overtone corresponds to (p + 1)th or (2p + 1)th harmonic. |
Question 41.
What is end correction ? State the cause of end correction. How is it estimated ?
Answer:
When sound waves are sent down the air column in a narrow closed or open pipe, they are reflected at the ends-without phase reversal at an open end and with a phase reversal at a closed end. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column. Thus, the stationary waves have an antinode at an open end.
However, because air molecules in the plane of an open end are not free to move in all directions, reflection of the longitudinal waves takes place slightly beyond the rim of the pipe at an open end. The distance of the antinode from the open end of the pipe is called end correction. According to Reynolds, the distance of the antinode from the rim is approximately 30% of the inner diameter of a cylindrical pipe. This distance must be taken into account in accurate determination of the wavelength of sound. Hence, this distance is called the end correction.
Therefore, if d is the inner diameter of a cylindrical pipe, an end correction e = 0.3 d for each open end must be added to the measured length of the pipe. If l is the measured length, the effective length of the air column in the case of a pipe closed at one end is l + 0.3d, while that for a pipe open at both ends is l + 0.6 d.
Question 42.
What are the frequencies of the notes produced in an open and closed pipes in terms of the length of pipe L and velocity of waves v?.
Answer:
The frequencies of all the harmonics present in an open pipe are
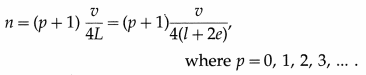
The frequencies of the odd harmonics present in a closed pipe are
![]()
where p = 0,1, 2, 3, … .
Question 43.
State the factors on which the fundamental frequency of air column in a pipe depends.
Answer:
- Speed of sound in air
- length of the pipe
- diameter of the pipe.
Question 44.
The fundamental frequency of air column in a pipe closed at one end is 300 Hz. What is the frequency of the
- second overtone
- third harmonic ? (Ignore the end correction.)
Answer:
Closed pipe.
- Second harmonic = fifth harmonic = 5 × 300 = 1500 Hz
- Third harmonic = 3 × 300 = 900 Hz.
Question 45.
The fundamental frequency of air column in a pipe open at both ends is 200 Hz. What is the frequency of the
- second harmonic
- third overtone ? (Ignore the end correction.)
Answer:
Open pipe.
- Second harmonic = 2 × 200 = 400 Hz
- Third overtone = fourth harmonic
= 4 × 200 = 800 Hz.
Question 46.
Stationary waves in the air column inside a pipe of length 50 cm and closed at one end have three nodes and three antinodes. What is the wavelength ?
Answer:
Here, L = 5\(\frac{\lambda}{4}\)
∴ Wavelength λ = \(\frac{4 L}{5}\) = \(\frac{4 \times 50 \mathrm{~cm}}{5}\) = 40 cm
Question 47.
Show that the fundamental frequency of vibration of the air column in a pipe open at both ends is double that of a pipe of the same length and closed at one end.
Answer:
Let LO and LC be the lengths of a pipe open at both ends and a pipe closed at one end, respectively. Let nO and nC be their corresponding fundamental frequencies. Then, ignoring the end corrections,
nO = \(\frac{v}{2 L_{\mathrm{O}}}\) and nC = \(\frac{v}{4 L_{\mathrm{C}}}\)
where v is the speed of the sound in air.
Given that LO = LC = L (say),
nO = \(\frac{v}{2 L}\) and nO = \(\frac{v}{4 L}\)
∴ nO = 2\(\left(\frac{v}{4 L}\right)\) = \(2 n_{\mathrm{C}}\)
Question 48.
Prove that a pipe of length 2L open at both ends has the same fundamental frequency as a pipe of length L closed at one end.
Answer:
Let LO and LC be the lengths of a pipe open at both ends and a pipe closed at one end, respectively. Let nO and nC be their corresponding fundamental frequencies. Then, ignoring the end corrections,
nO = \(\frac{v}{2 L_{\mathrm{O}}}\) and nC = \(\frac{v}{4 L_{\mathrm{C}}}\)
where v is the speed of the sound in air.
Given that LC = L and LO = 2L,
nO = \(\frac{v}{4 L}\) and nC = \(\frac{v}{4 L}\) ∴ nO = nC
Question 49.
A pipe open at both ends has the fundamental frequency n. If the pipe is immersed vertically in water up to half its length, what would be the fundamental frequency of the resulting air column?
Answer:
Let L be the length of the pipe open at both ends whose fundamental frequency is n. Then, ignoring the end correction, n = \(\frac{v}{2 L}\)
where v is the speed of sound in air.
When the pipe is immersed vertically in water up to half its length, it becomes a pipe closed at one end with an air column of length L’ = L / 2. Then, its fundamental frequency n’ is
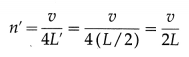
which is equal to n, the fundamental frequency of the open pipe.
![]()
Question 50.
The pth overtone of an organ pipe open at both ends has a frequency n. When one end of the pipe is closed, the qth overtone has a frequency N. Show that N = \(\frac{(2 q+1) n}{2(p+1)}\).
Answer:
Let L be the length of an organ pipe and v be the speed of sound in air.
When the pipe has both its ends open, the frequency of the pth overtone, ignoring the end correction, is (p + 1)\(\frac{v}{2 L}\).
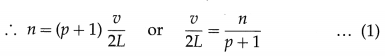
When one end of the pipe is closed, the frequency of the qth overtone of a pipe of length L and closed at one end is (2q + 1)\(\frac{v}{4 L}\)
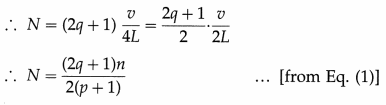
which is the required expression.
Question 51.
Two organ pipes open at both ends and of same length but different radii (or diameters) produce sounds of different frequencies. Why?
Answer:
Stationary waves formed in the air column of a pipe open at both ends have an antinode at each end. These antinodes are slightly beyond the rim of the pipe and an end correction of approximately 30% of the inner diameter must be added to the measured length of the air column for each open end.
Suppose two organ pipes, open at both ends and of same length 1, have inner diameters rf, and d2. Then, the effective lengths of the air columns are respectively L1 = l + 0.6dt and L2 = l + 0.6d2. The fundamental frequencies of the corresponding air columns are
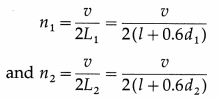
where v is the speed of sound in air. Thus, if d1 and d2 are different, n1 and n2 will also be different.
Question 52.
Two organ pipes closed at one end have the same diameters but different lengths. Show that the end correction at each end is e = \(\frac{n_{1} l_{1}-n_{2} l_{2}}{n_{2}-n_{1}}\), where the symbols have their usual meanings.
Answer:
Suppose two organ pipes, closed at one end and of the same inner diameter d, have lengths l1 and l2.
Then, the effective lengths of the air columns are respectively
L1 = l1 + 0.3d and L2 = l2 + e = l2 + 0.3d
where e = 0.3d is the end correction for the open end.
The fundamental frequencies of the corresponding air columns are
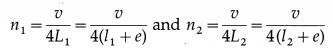
where v j the speed of sound in air.
∴ v = 4n1(l1 + e) = 4n1(l2 + e)
∴ n1I1 + n1e = n2I2 + n2e
∴ n1I1 – n2I2 = (n2 – n1)e
∴ e = \(\frac{n_{1} l_{1}-n_{2} l_{2}}{n_{2}-n_{1}}\)
which is the required expression.
Question 53.
State any two limitations of end correction.
Answer:
Limitations of end correction :
- Inner diameter of the tube must be uniform.
- Effects of air flow and temperature outside the tube are ignored.
- The prongs of the tuning fork should be perpendicular to the air column in the tube, with their tips at the centre of the tube and a small distance above the rim of the tube.
Question 54.
A tuning fork is in resonance with a closed pipe. But the same tuning fork cannot be in resonance with an open pipe of the same length. Why ?
Answer:
For the same length of air column, and the same speed of sound, the fundamental frequency of the air column in a closed pipe is half that in an open pipe. Hence, a tuning fork in unison with the air column in a closed pipe cannot be in unison with the air column of the same length in an open pipe.
Question 55.
Solve the following :
Question 1.
Calculate the fundamental frequency of an air column in a tube of length 25 cm closed at one end, if the speed of sound in air is 350 m/s.
Answer:
v = 350 m/s, L = 25 cm = 0.25 m
∴ The fundamental frequency of the air column is
n = \(\frac{v}{4 L}\) = \([\frac{350}{4 \times 0.25}/latex] = 350 Hz
Question 2.
A pipe which is open at both ends is 47 cm long and has an inner diameter of 5 cm. If the speed of sound in air is 348 m/s, calculate the fundamental frequency of the air column in that pipe.
Solution :
Data : l = 47 cm = 0.47 m, d = 5 cm = 0.05 m, v = 348 m/s
e = 0.3 d = 0.3 × 0.05 = 0.015 m
As the tube is open at both ends, the corrected length (L) is
L = l + 2e = 0.47 + (2 × 0.015) = 0.5 m
∴ The fundamental frequency of the air column is
n = [latex]\frac{v}{2 L}\) = \(\frac{348}{2 \times 0.5}\) = 348 Hz
Question 3.
A tube open at both ends is 47 cm long. Calculate the fundamental frequency of the air column. (Ignore the end correction. Speed of sound in air is 3.3 × 102 m/s.)
Solution :
Data : L = 47 cm = 0.47 m, v = 330 m/s.
The fundamental frequency of the air column,
n = \(\frac{v}{2 L}\) = \(\frac{330}{2 \times 0.47}\) = \(\frac{165}{0.47}\) = 351.1 Hz
Question 4.
The speed of sound in air at room temperature is 350 m/s. A pipe is 35 cm in length. Find the frequency of the third overtone in the pipe when it is
(i) closed at one end
(ii) open at both ends. Ignore the end correction.
Solution :
Data : v = 350 m/s, L = 35 cm = 35 × 10-2 m
(i) For a pipe closed at one end, the fundamental frequency is
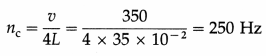
As only odd harmonics are present in this case, the frequency of pth overtone is np = (p × 2 + 1) nC
∴ The frequency of the 3rd overtone is
n3 = (3 × 2 + 1)nC = 7nC = 7 × 250 = 1750 Hz
![]()
(ii) For a pipe open at both ends, the fundamental frequency is
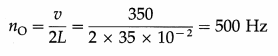
In this case, all harmonics are present.
∴ The frequency of the pth overtone is
np = (p + 1) nO
∴ The frequency of the 3rd overtone is n3 = (3 + 1) nO = 4nO = 4 × 500 = 2000 Hz
Question 5.
Find the frequency of the fifth overtone of an air column vibrating in a pipe closed at one end. The length of the pipe is 42.10 cm and the speed of sound in air at room temperature is 350 m/s. The inner diameter of the pipe is 3.5 cm.
Solution :
Data : L = 42.10 cm = 0.4210 m, v = 350 m/s, d = 3.5 cm = 3.5 × 10-2 m, pipe closed at one end

Question 6.
Determine the length of a pipe open at both ends which is in unison with a pipe of length 20 cm closed at one end, in the fundamental mode. Ignore the end correction.
Solution :
Let nO and LO be the fundamental frequency and length respectively, of the pipe open at both ends and let nC and LC be the corresponding values for a pipe closed at one end. If v is the speed of sound in air,
nO = \(\frac{v}{2 L_{\mathrm{O}}}\) and nC = \(\frac{v}{4 L_{\mathrm{C}}}\)
As the air columns in the two pipes vibrate in unison,
nO = nC
∴ 2LO = 4LC ∴ LO = 2LC
But LC = 20cm, ∴ LO = 2 × 20 = 40 cm
Question 7.
The fundamental frequency of an air column in a pipe closed at one end is in unison with the third overtone of an open pipe. Calculate the ratio of the lengths of their air columns.
Solution :
Pipe closed at one end : fundamental frequency,
nC = \(\frac{v}{4 L_{C}}\)
column is 51.8 cm.
nO = \(\frac{v}{2 L_{\mathrm{O}}}\)
In this case, the frequency of the third over-tone = \(\frac{4 v}{2 L_{\mathrm{O}}}\) = \(\frac{2 v}{L_{\mathrm{O}}}\)
By the data, \(\frac{v}{4 L_{C}}\) = \(\frac{2 v}{L_{\mathrm{O}}}\)
∴ \(\frac{L_{\mathrm{O}}}{L_{\mathrm{C}}}\) = 8 or \(\frac{L_{\mathrm{C}}}{L_{\mathrm{O}}}\) = \(\frac{1}{8}\)
Question 8.
The consecutive overtones of an air column closed at one end are 405 Hz and 675 Hz respectively. Find the fundamental frequency of a similar air column but open at both ends.
Solution:
For the air column closed at one end, let
L = the length of the air column,
nC = the fundamental frequency,
nq, nq + 1 = the frequencies of the qth and (q + 1)th overtones, where q = 1, 2, 3, …
Since only odd harmonics are present as overtones, nq = (2q + 1)nC and nq + 1 = [2(q + 1) + n]nC
= (2q + 3)nC
Data : nq = 405 Hz, nq+1 = 675 Hz
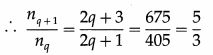
Solving for q, q = 1
Therefore, the two given frequencies correspond to the first and second overtones, i.e., the third and fifth harmonics.
∴ 3nC = 405 Hz
∴ nC = 135 Hz
This gives the fundamental frequency of the air column closed at one end.
The fundamental frequency (nO) of an air column of same length but open at both ends is double that of the air column closed at one end (ignoring the end correction).
∴ nO = 2nC = 2 × 135 = 270 Hz
This gives the fundamental frequency of a similar air column but open at both ends.
Solution :
Data : n = 480 Hz, l1 = 16.8 cm, l2 = 51.8 cm
(1) The speed of sound in air is v = 2n (l2 – l1)
= 2 × 480 × (51.8 – 16.8) = 33600 cm/s = 336 m/s
(2) Let λ be the wavelength of sound waves and e be the end correction.
For the first resonance, l1 + e = \(\frac{\lambda}{4}\) … (1)
For the second resonance, l2 + e = \(\frac{3 \lambda}{4}\) … (2)
From Eq. (1), λ = 4(l1 + e).
Substituting this value in Eq. (2), we get,
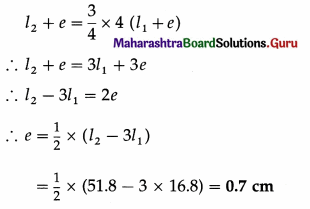
Question 9.
In a resonance tube experiment, a tuning fork v resonates with an air column 10 cm long and again resonates when it is 32.2 cm long. Calculate the wavelength of the wave and the end correction.
Solution:
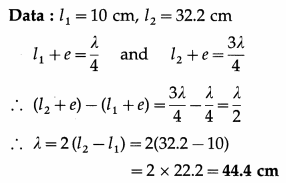
This gives the wavelength of the wave. We have,
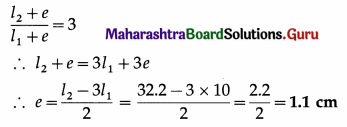
This gives the end correction.
Question 10.
The length of air column in a resonance tube for fundamental mode is 16 cm and that for second resonance is 50.25 cm. Find the end correction.
Solution:
Data: l1 = 16 cm, l2 = 50.25 cm
End correction,
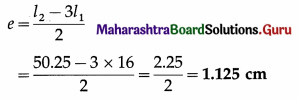
Question 56.
State the formula for the speed of transverse waves on a stretched string (or wire). Hence obtain an expression for the fundamental frequency of the vibrating string (or wire).
Answer:
- If a string (or a wire) stretched between two rigid supports is plucked at some point, the disturbance produced travels along the string in the form of transverse waves. If T is the tension applied to the string and m is the mass per unit length (i.e., linear density) of the string, the speed of the transverse waves is
v = \(\sqrt{\frac{T}{m}}\) - The transverse waves moving along the string are reflected from the supports. The reflected waves interfere and under certain conditions set up stationary waves in the string. At each support, a node is formed.
- The possible or allowed stationary waves are subject to the two boundary conditions that there must be a node at each fixed end of the string. The different ways in which the string can then vibrate are called its modes of vibration.
- In the simplest mode of vibration, there are only two nodes (N), one at each end and an antinode (A) is formed midway between them, as shown in
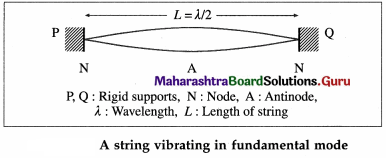
In this case, the distance between successive nodes is equal to the length of the string (L) and is equal to λ/2, where λ is the wavelength.
∴ L = \(\frac{\lambda}{2}\) or λ = 2L
The frequency of vibrations is n = \(\frac{v}{\lambda}\)
Substituting v = \(\sqrt{\frac{T}{m}}\) and λ = 2L in this relation, we get,
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\)
This is the lowest frequency of the stationary waves on a stretched string and is called the fundamental frequency.
Question 57.
What is the minimum frequency with which a stretched string of length L, linear density m can vibrate under tension T?
Answer:
The minimum frequency with which a stretched string of length L, linear density m can vibrate under tension T is the fundamental frequency given by n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\).
Question 58.
The mass per unit length of a wire is 1 × 10-4 kg/m and the tension in the wire is 25 N. What is the speed of the transverse waves on the wire?
Answer:
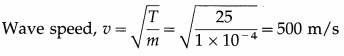
Question 59.
With neat labelled diagrams, explain the three lowest modes of vibration of a string stretched between rigid supports.
Answer:
Consider a string of linear density m stretched between two rigid supports a distance L apart. Let T be the tension in the string.
Stationary waves set up on the string are subjected to two boundary conditions : the displacement y = 0 at x = 0 and at x = L at all times. That is, there must be a node at each fixed end. These conditions limit the possible modes of vibration to only a discrete set of frequencies such that there are an integral number of loops p between the two fixed ends.
Since, the length of one loop (the distance between consecutive nodes) corresponds to half a wavelength (λ),
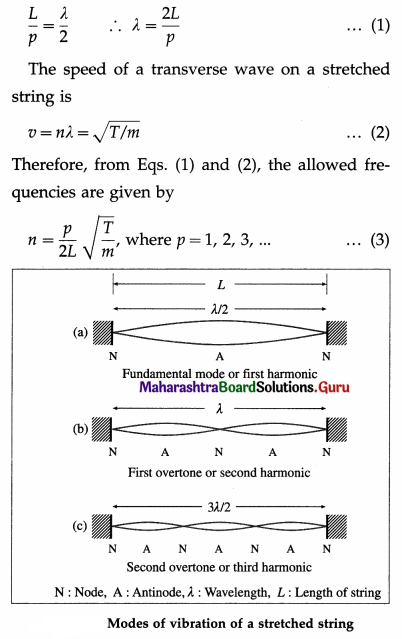
In the simplest mode of vibration, only one loop (p = 1) is formed. The corresponding lowest allowed frequency, n, given by
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\) … (4)
is called the fundamental frequency or the first harmonic. The possible modes of vibration with frequencies higher than the fundamental are called the overtones.
In the first overtone, two loops are formed (p = 2). Its frequency,
n1 = \(\frac{2}{L} \sqrt{\frac{T}{m}}\) = 2n … (5)
is twice the fundamental and is, therefore, the second harmonic.
In the second overtone, three loops are formed (p = 3). Its frequency,
n2 = \(\frac{3}{2 L} \sqrt{\frac{T}{m}}\) = 3n … (6)
is the third harmonic.
Question 60.
The speed of transverse waves on a vibrating string is 50 m/s. If the length of the string is 0.25 m, what is the fundamental frequency of vibration?
Answer:
Fundamental frequency, n = \(\frac{v}{(2 L)}\) = \(\frac{50}{(2 \times 0.25)}\)
= 100 Hz
![]()
Question 61.
State and explain the laws of vibrating strings.
Answer:
The fundamental frequency of vibration of a stretched string or wire of uniform cross section is 1
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\)
where L is the vibrating length, m the mass per unit length (linear density) of the string and T the tension in the string. From the above expression, we can state the following three laws of vibrating strings.
(1) Law of length : The fundamental frequency of vibrations of a stretched string is inversely proportional to its vibrating length, if the tension and mass per unit length are kept constant. If T and m are constant,
n ∝ \(\frac{1}{L}\) or nL = constant.
(2) Law of tension : The fundamental frequency of vibrations of a stretched string is directly proportional to the square root of the applied tension, if the length and mass per unit length are kept constant. If L and m are constant,
n ∝ or \(\sqrt{T}\) or n2/T = constant.
(3) Law of mass (or law of linear density) : The fundamental frequency of vibrations of a stretched string is inversely proportional to the square root of its mass per unit length, if the length and tension are kept constant. If L and T are constant,
n ∝ \(\frac{1}{\sqrt{m}}\) or n2m = constant.
Question 62.
How does the fundamental frequency of a vibrating string depend on the radius of cross section of the string and the mass density of the material of the string ?
Answer:
Consider a string stretched between two rigid supports a distance L apart. Let T be the tension in the string, r be its radius of cross section and p be the mass density of its material. Then, the mass of the string M = (πr2L)p, so that its linear density, i.e., mass per unit length, m = M/L = πr2p.
According to the law of mass of a vibrating string, the fundamental frequency (n) is inversely proportional to the square root of its linear density, when T and L are constant.

Question 63.
A string/wire is stretched between two rigid supports. State any two factors on which the fundamental frequency of the string/wire depends.
Answer:
- Tension in the string/wire
- length of the string/wire (or radius or mass per unit length or mass density of the material of the string/wire)
Question 64.
Why are strings of different thicknesses and materials used in a sitar or some other such instruments?
Answer:
The linear density of a string, m = πr2p, where r is the radius of cross section of the string and p is the mass density of its material. By the law of mass of a vibrating string, the frequency of vibrations n of the string is inversely proportional to \(\sqrt{m}\). Therefore, n ∝ \(\frac{1}{r}\) and n ∝\(\frac{1}{\sqrt{\rho}}\). Hence, the strings of different thicknesses and materials in a stringed musical instrument like sitar can be set to different scales.
Question 65.
If Y and ρ are Young’s modulus and mass density of the material of a stretched wire of length L, show that the fundamental frequency of vibration of the wire is n = \(\frac{1}{2 L} \sqrt{\frac{Y \Delta L}{\rho L}}\), where ∆L is the elastic extension of the wire.
Answer:
Consider a wire stretched between two rigid supports a distance L apart. Let T ≡ the tension in the wire, r ≡ the radius of cross section of the wire,
Y, ρ ≡ Young’s modulus and mass density of the material of the wire,
M,m ≡ the mass and linear density of the wire.
Then, M = (πr2L)ρ and m = \(\frac{M}{L}\) = πr2ρ … (1)
The stress in the wire = \(\frac{T}{\pi r^{2}}\)
∴ \(\frac{T}{m}\) = \(\frac{T}{\pi r^{2} \rho}\) = \(\frac{\text { stress }}{\rho}\) … (2)
The The fundamental frequency of vibration of the wire,

if ∆L is the elastic extension of the wire under tension T, strain = ∆L/L.
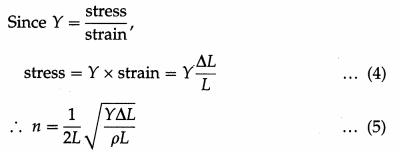
which is the required expression.
Question 66.
What is the linear density of a wire of mass density 8 g/cm3 and cross-sectional radius 0.05 mm ?
Answer:
Linear density of the wire = nr2p
= π(5 × 10-3)2 (8) = 2π × 10-4 g/cm.
Question 67.
Stationary waves on a vibrating string of length 30 cm has three loops. What is the wavelength ?
Answer:
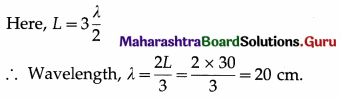
Question 68.
Write a short note on sonometer.
Answer:
A sonometer consists of a uniform wire stretched over a rectangular sounding box, and passes over
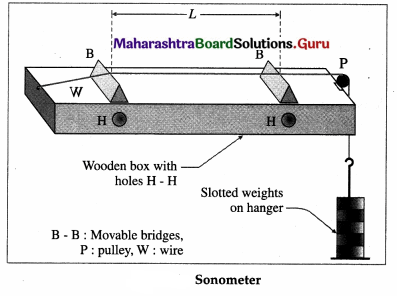
two movable bridges (or knife edges) and a pulley, in above figure. It works on the phenomenon of resonance. The tension in the wire is adjusted by adding weights to the hanger attached to the free end of the wire. The length of the wire between the movable bridges, L, is adjusted to vibrate in unison with a given timing fork either by beats method or by paper-rider method. L is called the vibrating length. First, the vibrating length is set to minimum and then gradually increased in small steps. In the beats method, the wire and the tuning fork are simultaneously set into vibrations for each vibrating length. Beats can be heard when the two frequencies are very close. Then, a finer adjustment of the wire is needed so that no beats are heard. This is when the two are in unison.
For the paper-rider method, a small light paper in the form of Λ is placed on the wire at its centre. The stem of the vibrating timing fork is gently pressed on the sonometer box. The vibrating length is gradually increased from minimum till the paper rider vibrates and thrown off. Because, when the wire resonates with the tuning fork at its lowest fundamental mode, the wire vibrates with maximum amplitude and the centre of the wire is an antinode. Hence, the paper rider is thrown off.
A sonometer is used to determine the frequency of a tuning fork and to verify the laws of vibrating strings.
Question 69.
Explain the use of a sonometer to verify
(i) the law of length
(ii) the law of tension
(iii) the law of linear density.
Answer:
(i) Verification of law of length : According to this law, n ∝ \(\frac{1}{L}\), if T and m are constant. To verify this
law, the sonometer wire of given linear density m is kept under constant tension T. The length of the wire is adjusted for the wire to vibrate in unison with tuning forks of different frequencies n1, n2, n3,… . Let L1, L2, L3, … be the corresponding resonating lengths of the wire. It is found that, within experimental errors, n1L1 = n2L2 = n3L3 = …. This implies that the product, nL = constant, which vertifies the law of length.
(ii) Verification of law of tension : According to this law, n ∝ \(\sqrt{T}\), if L and m are constant. To verify this law, the vibrating length L of the sonometer wire of given linear density m is kept constant.
A set of tuning forks of different frequencies is used. The tension in the wire is adjusted for the wire to vibrate in unison with tuning forks of different frequencies n1, n2, n3,….. . T1, T2, T3, ….. corresponding tensions. It is found that, within experimental errors, \(\frac{n_{1}}{\sqrt{T_{1}}}\) = \(\frac{n_{2}}{\sqrt{T_{2}}}\) = \(\frac{n_{3}}{\sqrt{T_{3}}}\) = ….. This implies \(\frac{n_{1}}{\sqrt{T}}\) = constant which verifies the law of tension.
(iii) Verification of linear density : According to this law, n ∝ \(\frac{1}{\sqrt{m}}\), if T and L are constant. To verify this law, two wires having different linear densities m1 and m2 are kept under constant tension T.
A tuning fork of frequency n is used. The lengths of the wires are adjusted for the wires to vibrate in unison with the tuning fork. Let L1 and L2 be the corresponding resonating lengths of the wires. It is found that, within experimental errors, \(L_{1} \sqrt{m_{1}}\) = \(L_{2} \sqrt{m_{2}}\). This implies \(L \sqrt{m}\) = constant. According to the law of length of a vibrating string, n ∝ \(\frac{1}{L}\).
∴ n ∝ \(\frac{1}{\sqrt{m}}\) which verifies the law of linear density.
Question 70.
A stretched sonometer wire vibrates at 256 Hz. If its length is increased by 10%, without changing the tension in the wire, what will be the frequency of the wire ?
Answer:
L2 = 1.1 L1 = \(\frac{n_{2}}{n_{1}}\) = \(\frac{L_{2}}{L_{1}}\) ∴ \(\frac{n_{2}}{256}\) = 1.1
∴ n2 = 256 × 1.1 = 281.6 Hz
Question 71.
Solve the following :
Question 1.
Find the speed of a transverse wave along a string of linear density 3.6 × 10-3 kg/m, when it is under a tension of 1.8 kg wt.
Solution :
Data : m = 3.6 × 10-3 kg/m, g = 9.8 m/s2
∴ T = 1.8 kg wt = 1.8 × 9.8N
The speed of transverse waves along the string is
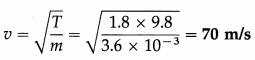
![]()
Question 2.
The speed of a transverse wave along a uniform metal wire, when it is under a tension of 1000 g wt, is 68 m/s. If the density of the metal is 7900 kg/m3, find the area of cross section of the wire.
Solution :
Data : g = 9.8 m/s2, T = 1000 g wt = 1 kg wt = 9.8 N,
V = 68 m/s, ρ = 7900 kg/m3

This gives the area of cross section of the wire.
Question 3.
A transverse wave is produced on a string 0.7 m long and fixed at its ends. Find the speed of the wave when it vibrates emitting the second overtone of frequency 300 Hz.
Solution :
Data : L = 0.7 m, n (second overtone) = 300 Hz
In this case, three loops are formed on the string.
∴ L = 3\(\frac{\lambda}{2}\)
∴ λ = \(\frac{2 L}{3}\) ∴ v = nλ = \(\frac{2}{3}\)nL
∴ v = \(\frac{2}{3}\) × 300 × 0.7 = 140 m/s
This gives the speed of the wave.
Question 4.
A uniform wire under tension is fixed at its ends. If the ratio of the tension in the wire to the square of its length is 360 dyn/cm2 and the fundamental frequency of vibration of the wire is 300 Hz, find its linear density.
Solution :

Question 5.
A metal wire of length 20 cm and diameter 0.2 mm is stretched by a load of 2 kg wt. If the density of the material of the wire is 7.8 g/cm3, find the fundamental frequency of vibration of the wire.
Solution :
Data : L = 20 cm = 0.2 m, d = 0.2 mm, g = 9.8 m/s2, T = 2 kg wt = 2 × 9.8 N = 19.6 N, ρ = 7.8 g/cm3 = 7.8 × 103 kg/m3
∴ r = \(\frac{d}{2}\) = 0.1 mm = 0.1 × 10-3 m
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\) and m = πr2ρ
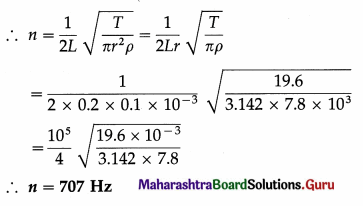
The fundamental frequency of vibration of the wire is 707 Hz.
Question 6.
Two wires, each 1 m long and of the same diameter, have densities 8 × 103 kg/m3 and 2 × 103 kg/m3 and are stretched by tensions 196 N and 49 N, respectively. Compare their fundamental frequencies.
Solution :
Data : L1 = L2 = 1 m, d1 = d2 (∴ r1 = r2), ρ1 = 8 × 103 kg/m3, ρ2 = 2 × 103 kg/m3, T1 = 196 N, T2 = 49N

∴ Their fundamental frequencies are the same.
Question 7.
A uniform wire of length 49 cm and linear density 4 × 10-4 kg/m is subjected to a tension of 28 N. Determine its frequency for
- the fundamental mode
- the second harmonic
- the third overtone.
Solution :
Data : L = 49 cm = 0.49 m, T = 28 N, m = 4 × 10-4 kg/m
- Fundamental frequency :
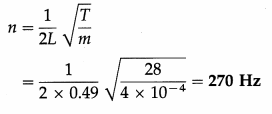
- Second harmonic : 2n = 2 × 270 = 540 Hz
- Third overtone : 4n = 4 × 270 = 1080 Hz
Question 8.
Two wires of the same material, having lengths in the ratio 2 : 1 and diameters in the ratio 3 :1 are subjected to tensions in the ratio 1 : 4. Find the ratio of their fundamental frequencies.
Solution :
Let n1, L1, T1, m1, r1 and ρ1 be the fundamental frequency, vibrating length, tension, mass per unit length, radius and density of the first wire respectively and let n2, L2, T2, m2, r2 and ρ2 be the corresponding quantities of the second wire.

Substituting these values in the above relation,
\(\frac{n_{1}}{n_{2}}\) = \(\frac{1}{2}\) × \(\frac{1}{3}\) × \(\sqrt{\frac{1}{4} \times 1}\) = \(\frac{1}{12}\)
Question 9.
A wire under a certain tension, gives a note of fundamental frequency 320 Hz. When the tension is changed, the frequency of the fundamental note rises to 480 Hz. Compare the tensions in the wire.
Solution :
Data : n1 = 320 Hz, n2 = 480 Hz Fundamental frequency is n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\)
As the length (L) of the wire and its mass per unit length (m) are kept constant,
n ∝ \(\sqrt{T}\)
∴\(\frac{n_{1}}{n_{2}}\) = \(\sqrt{\frac{T_{1}}{T_{2}}}\)
∴ The ratio of the tensions in the wire,
\(\frac{T_{1}}{T_{2}}\) = \(\left(\frac{n_{1}}{n_{2}}\right)^{2}\) = \(\left(\frac{320}{480}\right)^{2}\) = \(\left(\frac{2}{3}\right)^{2}\) = \(\frac{4}{9}\)
Question 10.
A transverse wave is produced on a stretched string 0.9 m long and fixed at its ends. Find the speed of the transverse wave, when the string vibrates while emitting second overtone of frequency 324 Hz.
Solution :
Data : L = 0.9 m, n (second overtone) = 324 Hz
For the second overtone of a vibrating string, λ = \(\frac{2}{3}\)L
The speed of the transverse wave formed on the string, v = nλ
∴ v = n × \(\frac{2}{3}\)L = 324 × \(\frac{2}{3}\) × 0.9
= 324 × 0.6 = 194.4 m/s
Question 11.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string ?
Solution :
Data : L1 = 80 cm n1 = 112 Hz, n2 = 160 Hz
According to the law of length, n1L1 = n2L2.
∴ The vibrating length to produce the fundamental frequency of 160 Hz,
L2 = \(\frac{n_{1} L_{1}}{n_{2}}\) = \(\frac{112(80)}{160}\) = 56 cm
Question 12.
What should be the tension applied to a wire of length 1 m and mass 10 grams, if it has to vibrate with the fundamental frequency of 50 Hz ?
Solution :
Data : L = 1 m, mass of the wire = 10 g = 0.01 kg, n = 50 Hz
∴ m = mass per unit length of the wire = \(\frac{0.01}{1}\)
= 0.01 kg/m
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\)
∴ Tension = T = 4n2L2m
= 40(50)2(1)2(0.01)
= 4 × 2500 × 0.01 = 100 N
Question 13.
A sonometer wire of length 1 m weighing 2 g is subjected to a suitable tension. The vibrating length of the wire in unison with a tuning fork of frequency 512 Hz is 12 cm. If the vibrating length of the wire in unison with another fork under the same conditions is 12.8 cm, find the frequency of this fork.
Solution :
Data : L1 = 12 cm, n1 = 512 Hz, L2 = 12.8 cm n1L1 = n2L2
∴ The frequency of the second fork,
n2 = \(\frac{n_{1} L_{1}}{L_{2}}\) = \(\frac{512(12)}{12.8}\) = 480 Hz
![]()
Question 14.
A stretched sonometer wire emits a fundamental note of frequency 256 Hz. Keeping the stretching force constant and reducing the length of the wire by 10 cm, the frequency becomes 320 Hz. Calculate the original length of the wire.
Solution:
Data : n1 = 256 Hz, T and m constant, L2 = L1 – 10 cm, n2 = 320 Hz
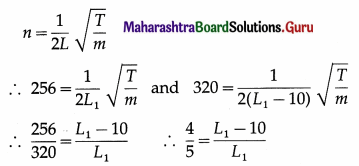
∴ 5L1 – 50 = 4L1
∴ L1 = 50 cm = 0.5 m
Alternative method :
Since T and m are constant, nL = constant.
∴ n1L1 = n2L2 ∴ \(\frac{L_{1}}{L_{2}}\) = \(\frac{n_{2}}{n_{1}}\)
∴ \(\frac{L_{1}}{L_{1}-10}\) = \(\frac{320}{256}\) = \(\frac{20}{16}\) = \(\frac{5}{4}\)
∴ 4L1 = 5L1 – 50
∴ 5L1 – 4L1 = 50
∴L1 = 50cm = 0.5 m
Question 15.
A sonometer wire, 36 cm long, vibrates with a frequency of 280 Hz in the fundamental mode when it is under a tension of 24.5 N. Calculate the linear density of the material of the wire.
Solution :
Data: L = 36 cm = 0.36 m, n = 280 Hz, T = 24.5 N,

Question 16.
A sonometer wire 36 cm long, vibrates with a fundamental frequency of 280 Hz, when it is under tension of 24.5 N. Calculate mass per unit length of wire.
Solution :
Data : L = 36 cm = 0.36 m, n = 280 Hz, T = 24.5 N
n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}\)
∴ Linear density, m = \(\frac{T}{4 L^{2} n^{2}}\)
∴ m = \(\frac{24.5}{4(0.36)^{2}(280)^{2}}\)
= 6.0 × 10-4 kg/m
Question 17.
The length of a sonometer wire between two fixed ends is 110 cm. Where should be the two bridges be placed so as to divide the wire into three segments, whose fundamental frequencies are in the ratio of 1: 2 : 3 ?
Solution :
Data : L1 + L2 + L3 = 110 cm, n1 : n2 : n3 = 1 : 2 : 3
According to the first law of length, n ∝ \(\frac{1}{L}\) if T and m are constant.
By given data, n1 = 2n2 = 3n3
∴ \(\frac{1}{L_{1}}\) = \(\frac{2}{L_{2}}\) = \(\frac{3}{L_{3}}\)
∴ L2 = 2L1 and L3 = 3L1
L1 + 2L1 + 3L1 = 110
∴ 6L1 = 110
∴ L1 = 18.3 cm
∴ L2 = 2 × 18.3 = 36.6 cm
∴ L3 = 3 × 18.3 = 54.9 cm
Therefore, the two bridge should be kept in such a way that the distance between them in 36.6 cm and distance of 1st bridge from the fixed end of the wire is 18.3 cm.
Question 72.
What are beats? Define
(1) the period of beats
(2) beat frequency (1 mark each)
Answer:
A periodic variation in loudness (or intensity) when two sound notes of slightly different frequencies are sounded
at the same time is called beats.
If two notes of slightly different frequencies n1 and n2 are played simultaneously, the resulting
note from their interference has a frequency of (n1 + n2)/2. However, the amplitude of this resulting note varies from the sum to the difference of the amplitudes of the two notes n1 and n2. An intensity maximum and an intensity minimum are respectively called waxing and waning. Thus, the resulting note will be heard as one of periodic loud (waxing) and faint (waning) sound. One waxing and one waning form one beat. Formation of beats is an example of interference in time.
The time interval between successive maxima or minima of sound at a given place is called the period of beats.
The number of beats produced per unit time is called the beat frequency.
Question 73.
Distinguish between stationary waves and beats. (Two points of distinction)
Answer:
|
Stationary waves |
Beats |
| 1. These are formed due to interference, under certain conditions, between two identical progressive waves travelling in opposite directions. | 1. These are formed due to interference between two progressive waves which need not be travelling in opposite directions. |
| 2. Interfering waves must have the same frequency. | 2. Interfering waves must have slightly different frequencies. |
| 3. At a given point, the amplitude is constant. | 3. At a given point, the amplitude changes with time. |
| 4. Nodes and antinodes are produced. | 4. There is waxing and waning of resultant intensity. |
| 5. The resultant wave does not travel in any direction. | 5. The resultant wave travels in the forward direction. |
| 6. There is no energy transport through the medium. | 6. There is energy transport through the medium. |
Question 74.
Discuss analytically the formation of beats and show that
(1) the beat frequency equals the difference in frequencies of two interfering waves
(2) the waxing and waning occur alternately and with the same period.
OR
Explain the production of beats and deduce analytically the expression for beat frequency.
Answer:
Consider two sound waves of equal amplitude (A) and slightly different frequencies n1 and n2 (with n1 > n2) propagating through the medium in the same direction and along the same line. These waves can be represented by the equations y1 = A sin 2πn1t and y2 = A sin 2πn2t at x = 0, where y denotes the displacement of the particle of the medium from its mean position.
By the principle of superposition of waves, the resultant displacement of the particle of the medium at the point at which the two waves arrive simultaneously is the algebraic sum
y = y1 + y2 = A sin 2πn1t + A sin 2πn2t
Now, sin C + sin D
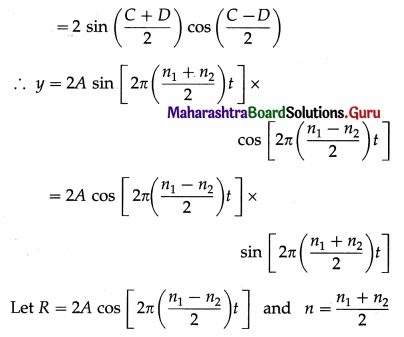
∴y = R sin 2πnt
The above equation shows that the resultant motion has amplitude IRI which changes periodically with time. The period of beats is the period of waxing (maximum intensity of sound) or the period of waning (minimum intensity of sound). The intensity of sound is directly proportional to the square of the amplitude of the wave. It is maximum (waxing) when R becomes maximum;

The intensity of sound is minimum (waning) when R = 0

From Eqs. (1) and (2), it can be seen that the waxing and waning occur alternately and with the same period.
Question 75.
The speed of sound in air under certain conditions is 350 m/s. If two sound waves of wavelengths \(\) m and \(\) m arrive at a point at the same time, what will be the beat frequency?
Answer:
Beat frequency = |n1 – n2|
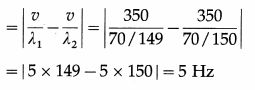
Question 76.
State the conditions for hearing beats.
Answer:
Conditions for hearing beats : For two sound waves to interfere and give rise to beats,
- they should travel in the same medium and arrive at the listener at the same time
- their frequencies should not differ by more than about 7 Hz for distinct beats
- their amplitudes should be equal or nearly so.
Question 77.
When two tuning forks of slightly different frequencies are sounded together to produce beats, what is the effect on the beat frequency if the prongs of the tuning fork with higher frequency are waxed a little or filed a little?
Answer:
Filing the prongs of a tuning fork reduces its mass and thereby raises its frequency. Applying a little wax to the prongs increases its mass and thereby reduces its frequency. Therefore, filing the prongs of the tuning fork of the higher frequency increases the beat frequency while applying a little wax to its prongs decreases the beat frequency.
Question 78.
When two tuning forks of slightly different frequencies are sounded together to produce beats, what is the effect on beat frequency if the prongs of the tuning fork with lower frequency is waxed a little or filed a little?
Answer:
Filing the prongs of a tuning fork reduces its mass and thereby raises its frequency. Applying a little wax to the prongs increases its mass and thereby reduces its frequency. Therefore, filing the prongs of the tuning fork of the lower frequency decreases the beat frequency while applying a little wax to its prongs increases the beat frequency.
Question 79.
A tuning fork has frequency 512 Hz. What can you say about its frequency when
- its prongs are filed
- some wax is applied to its prongs ?
Answer:
- Its frequency will be more than 512 Hz.
- Its frequency will be less than 512 Hz.
![]()
Question 80.
Explain any two applications of beats.
Answer:
Applications of beats :
(1) Listening for beats – or rather, their absence-is the usual method of tuning musical instruments and in the determination of the frequency of a musical note.
(2) Ultrasonic vocal sounds made by bats and dolphins may be detected by superimposing a sound of different frequency to produce audible beats.
(3) In music, beats are used to produce a low frequency sound (a grave tone). Two notes whose difference in frequency is equal to the desired low frequency are used for this purpose. When two notes are nearly in tune, the beats are slow. But as the beat frequency increases to 20 Hz or more, the beats may ultimately merge into a continuous tone known as a difference tone.
(4) (i) Speed of a moving object can be determined using a Doppler RADAR. Radio waves from the RADAR are reflected off a moving object, such as an aeroplane. The superposition of the incident and reflected waves produces beats. The frequency of beats helps to determine the speed of the aeroplane.
The same principle is used in speed guns used by traffic police to determine the speed of cars on a highway.
(ii) In medicine, a Doppler ultrasound test (sonography) uses reflected sound waves to evaluate blood flow through the major arteries and veins of the arms, legs and neck. It can show blocked or reduced blood flow because of narrowing of the major arteries. Duplex (or 2D) Doppler, Colour Doppler and Power Doppler are different techniques of the same test.
Notes: Some other applications of beats are as follows :
- Detection of toxic gases inside mines, especially collieries : Air from inside a mine and pure air are blown through two separate identical organ pipes. If beats are heard it would indicate that the composition of air inside the mines is different from that outside. This can serve as an early warning system.
- In music, consonance and dissonance depend upon the beats produced when two notes are sounded simultaneously. A beat frequency between 10 Hz and 50 Hz (between the fundamental notes being played as well as any of their overtones) is unpleasant and results in dissonance.
- Superheterodyne reception of radio waves in most radio, television and radar receivers : A low-frequency signal produced in the receiver is beat against an incoming high-frequency radio signal to produce an intermediate (beat) frequency (IF). This IF signal retains the information of the incoming signal. The receiver can be tuned to different broadcast frequencies by adjusting the frequency of the low-frequency signal. The IF signal though can be kept the same in every case and can therefore be amplified with higher gain.]
Question 81.
If beat frequency is 10 Hz, what is the time interval between
(i) successive waxings
(ii) a waxing and subsequent waning of sound.
Answer:
Beat period = \(\frac{1}{\text { beat frequency }}\) = \(\frac{1}{10 \mathrm{~Hz}}\) = 0.1 s
Hence, the time interval will be 0.1 s in case (i) and 0.05 s in case (ii).
Question 82.
A sonometer wire of length L1 is in unison with a tuning fork of frequency n. When the vibrating length of the wire is reduced to L2, it produces x beats per second with the fork. Show that n = x2.\(\frac{L_{2}}{L_{1}-L_{2}}\).
Answer:
The fundamental frequency of vibration of a wire of length L1, mass per unit length m and under tension T is
n1 = \(\frac{1}{2 L_{1}} \sqrt{\frac{T}{m}}\) = n … (1)
since it is in unison with a tuning fork of frequency n. When the vibrating length of the wire is L2, its fundamental frequency is
n2 = \(\frac{1}{2 L_{2}} \sqrt{\frac{T}{m}}\) … (2)
T and m remaining constant.
∴ \(\frac{n_{2}}{n_{1}}[latex] = [latex]\frac{L_{1}}{L_{2}}[latex] … (3)
Since L2 < L1, n2 > n1 so that n2 – n1 = x
∴ n2 = n1 + x …. (4)
Substituting for n2 in Eq. (3),
[latex]\frac{n_{1}+x}{n_{1}}\) = \(\frac{L_{1}}{L_{2}}\) or \(\frac{x}{n_{1}}\) = \(\frac{L_{1}-L_{2}}{L_{2}}\)
∴ n1 = n = x.\(\frac{L_{2}}{L_{1}-L_{2}}\)
which is the required expression.
Question 83.
Solve the following :
Question 1.
A tuning fork C produces 6 beats/second- with another tuning fork D of frequency 320 Hz. When a little wax is put on the prongs of D, the number of beats reduces to 4 per second. Find the frequency of C.
Solution :
- Initially 6 beats per second are heard. Hence, the difference between the frequencies of the tuning forks is 6 Hz. As the frequency of fork D is 320 Hz, the frequency of fork C = 320 + 6 Hz
= 326 Hz or 314 Hz - When the prongs of fork D are loaded with a little wax, the frequency of fork D decreases and becomes less than 320 Hz.
- If the frequency of fork C is 326 Hz, the number of beats heard per second must increase.
- However, as the number of beats heard per second has decreased from 6 to 4, the frequency of fork C must be 314 Hz.
Question 2.
A tuning fork C produces 8 beats per second with another tuning fork D of frequency 340 Hz. When the prongs of tuning fork C are filed a little, the number of beats produced per second decreases to 4. Find the frequency of tuning fork C before filing its prongs.
Solution :
The frequency of timing fork D is 340 Hz. Let n be the frequency of tuning fork C. Since tuning forks C and D produce 8 beats per second when sounded together,
n – 340 = 8 or 340 – n = 8
∴ n = 348 Hz or 332 Hz
When the prongs of a tuning fork are filed a little, its frequency increases. Let n’ be its frequency after filing : n’ > n.
It is given that the beat frequency is reduced from 8 Hz to 4 Hz.
If n was 348 Hz, n’ will be more than 348 Hz. Hence, the beat frequency should increase. Hence, n ≠ 348 Hz.
∴ n = 332 Hz
Question 3.
A sonometer wire 100 cm long produces a resonance with a tuning fork. When its length is decreased by 10 cm, 8 beats per second are heard. Find the frequency of the tuning fork.
Solution :
Data : L1 = 100 cm, L2 = 100 – 10 = 90 cm, n2 – n1 = 8 beats per second
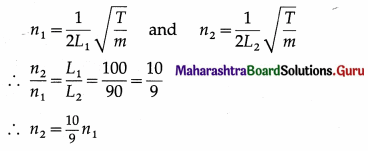
Now, n2 – n1 = 8 ∴ \(\frac{10}{9}\)n1 – n1 = 8
∴ 10n1 – 9n1 = 9 × 8 = 72
∴ n1 = 72 Hz
This gives the frequency of the tuning fork as the wire of length 100 cm is in unison with the fork.
Question 4.
A stretched sonometer wire is in unison with a tuning fork. When its length is increased by 4 %, the number of beats heard per second is 6. Find the frequency of the fork.
Solution :
Data : \(\frac{L_{2}}{L_{1}}\) = 1.04, n1 – n2 = 6Hz
n1 = \(\frac{1}{2 L_{1}} \sqrt{\frac{T}{m}}\) and n2 = \(\frac{1}{2 L_{2}} \sqrt{\frac{T}{m}}\)
∴ \(\frac{n_{1}}{n_{2}}\) = \(\frac{L_{2}}{L_{1}}\) = 1.04
∴ n1 = 1.04n2
Now, n1 – n2 = 6
∴ 1.04 n2 – n2 = 6
∴ n2 = \(\frac{6}{0.04}\) = 150 Hz
∴ n1 = n2 + 6 = 150 + 6 = 156 Hz
This gives the frequency of the tuning fork as initially the wire and the fork vibrate in unison.
Question 5.
The wavelengths of two notes in air are \(\frac{83}{170}\) m and \(\frac{83}{172}\) m. Each of these notes produces 4 beats per second with a third note of a fixed frequency. Find the speed of sound in air.
Solution :
Data : λ1 = 83/170 m, λ2 = 83/172 m
Let n1 and n2 be the corresponding frequencies.
∴ v = n1λ1 = n2λ2
where v is the speed of sound in air.
But λ1 > λ2
∴ n1 < n2
If n is the third frequency, n1 < n < n2
∴ n – n1 = 4 and n2 – n = 4
Method 1 :
∴ n2 – n1 = 8 ∴ \(\frac{v}{\lambda_{2}}\) – \(\frac{v}{\lambda_{1}}\) = 8
∴ v\(\left[\frac{172}{83}-\frac{170}{183}\right]\) = 8 ∴ v × \(\frac{2}{83}\) = 8
∴ v = 4 × 83 = 332 m/s
Method 2 :
∴ n1 = n – 4 and n2 = n + 4
∴ (n – 4) × \(\frac{83}{170}\) = (n + 4) × \(\frac{83}{172}\)
Simplifying, we get, 2n = 1368
∴ n = 684 Hz
∴ n1 = 684 – 4 = 680 Hz
∴ v = n1λ1 = 680 × \(\frac{83}{170}\) = 4 × 83
∴ v = 332 m/s
Question 6.
Two sound notes have wavelengths \(\frac{83}{170}\) m and \(\frac{83}{172}\) m in air. These notes, when sounded together, produce 8 beats per second. Calculate the velocity of sound in air and frequencies of the two notes.
Solution :
Data : λ1 = 83/170 m, λ2 = 83/172 m
Let nλ1 and nλ2 be the corresponding frequencies.
∴ v = n1λ1 = n2λ2
where v is the velocity of sound in air.
∴ n1 = \(\frac{v}{\lambda_{1}}\) and n2 = \(\frac{v}{\lambda_{2}}\) … (1)
But λ1 > λ2 ∴ n1 < n2
∴ n2 – n1 = 8
∴ v\(\left(\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{1}}\right)\) = 8 [From Eq. (1)] …(2)
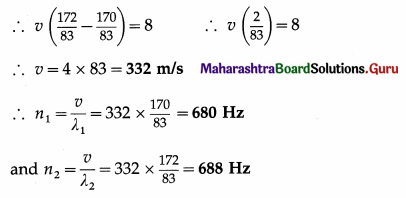
Question 7.
32 tuning forks are arranged in descending order of frequencies. If any two consecutive tuning forks are sounded together, the number of beats heard is eight per second. The frequency of the first tuning fork is octave of the last fork. Calculate the frequency of the first, last and the 21st fork.
Solution :
Data : n1 = 2n32, (n1 is octave of n32) beat frequency = 8 Hz
The set of tuning forks is arranged in descending order of their frequencies.
∴ n2 = n1 – 8
n3 = n2 – 8 = n1 – 2 × 8
n4 = n3 – 8 = n1 – 3 × 8
∴ n32 = n1 – 31 × 8 = n1 – 248
Since n1 = 2n31, n32 = 2n32 – 248
∴ The frequency of the last fork, n32 = 248 Hz
The frequency of the first fork, n1 = 2n32 = 2 × 248 = 496 Hz
∴ The frequency of the 21st fork, n21 = n1 – 20 × 8 = 496 -160 = 336 Hz
![]()
Question 8.
A set of 12 tuning forks is arranged in order of increasing frequencies. Each fork produces V beats per second with the previous one. The last is an octave of the first. The fifth fork has a frequency of 90 Hz. Find V and the frequency of the first and the last tuning forks.
Solution :
Data : ni+1 – ni = Y, n12 = 2n1, n5 = 90 Hz n2 – n1 = Y beats/s
∴ n2 = n1 + Y beats/s
Similarly, n3 = n2 + Y = n1 + Y + Y
∴ n3 = n1 + 2Y = n1 + (3 – 1) Y
∴ nx = n1 + (x – 1) Y
Similarly, n12 = n1 + (12 – 1) Y = n1 + 11Y
∴ n12 = 2n1 = n1 + 11Y
∴ n1 = 11Y
Also, n5 = n1 + (5 – 1) Y = n1 + 4Y
∴ n5 = 11Y + 4Y = 15Y
∵ n5 = 90 Hz ∴ 15Y = 90 ∴ Y = 6
∴ n1 = 11Y beats/s = 11 × 6 beats/s = 66 Hz and n12 = 2n1 = 2 (66) = 132 Hz
Question 9.
Two tuning forks when sounded together produce 5 beats per second. A sonometer wire of length 0.24 m is in unison with one of the forks. When the length of wire is increased by 1 cm, it is in unison with the other fork. Find the frequencies of the tuning forks.
Solution :
Data :L1 = 0.24 m = 24 cm, L2 = 24 + 1 = 25 cm, beat frequency = 5 Hz
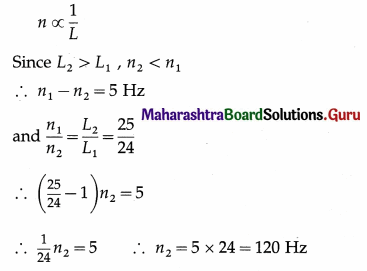
∴ n1 = n2 + 5 = 125 Hz
∴ The frequencies of the two tuning forks are 125 Hz and 120 Hz.
Question 10.
A closed pipe and an open pipe sounded together produce 5 beats/s. If the length of the open pipe is 30 cm, find by how much should the length of the closed pipe be changed to make the air columns in the two pipes vibrate in unison. [Speed of sound in air = 330 m/s]
Solution :
Data : Beat frequency = 5 s-1, LO = 0.3 m, v = 330 m/s
The fundamental frequencies of a closed pipe and open pipe are respectively
nC = \(\frac{v}{4 L_{\mathrm{C}}}\) and n0 = \(\frac{v}{2 L_{O}}\)
Let L’C and n’C be the changed length and frequency of the closed pipe,
n’C = nO
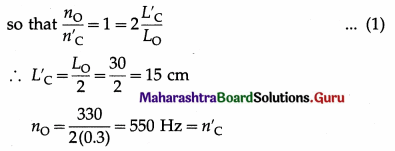
Method 1 :
Since the beat frequency = 5 Hz,
|nC – nO| = |nC – n’C| = 5
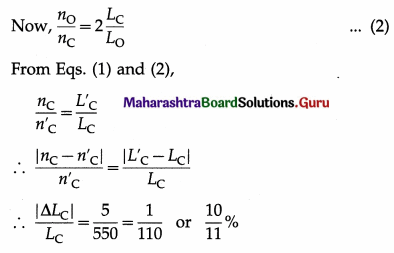
∴ The length of the given closed pipe should be changed by \(\frac{10}{11}\) % to bring it unison with the open pipe.
Method 2 :
Since the beat frequency = 5 Hz,
nC – nO = 5 or nO – nC = 5
i. e., nC = 555 Hz or 545 Hz
∴ LC = \(\frac{v}{4 n_{\mathrm{C}}}\) = \(\frac{330}{4(555)}\) or \(\frac{330}{4(545)}\)
= 0.1486 m or 0.1514 m
= 14.86 cm or 15.14 cm
∴ The length of the given closed pipe should be changed by 0.14 cm.
Question 11.
The forks, A and B, produce 4 beats/s when sounded together. Fork A is in unison with 30 cm length of a sonometer wire and fork B is in unison with 25 cm length of the same wire under the same tension. Calculate the frequencies of the forks.
Solution :
Data : LA = 30 cm, LB = 25 cm, beat frequency = 4 s-1
n ∝ \(\frac{1}{L}\)
Since LA > LB, nA < nB
∴ nB – nA = 4 Hz
and, for the same tension and linear density,
\(\frac{n_{\mathrm{B}}}{n_{\mathrm{A}}}\) = \(\frac{L_{\mathrm{A}}}{L_{\mathrm{B}}}\) = \(\frac{30}{25}\) = \(\frac{6}{5}\)
∴ \(\left(\frac{6}{5}-1\right)\)nA = 4
∴ \(\frac{1}{5}\)nA = 4
∴ nA = 20 Hz
∴ nB = 24 Hz
Question 84.
Explain the following characteristics of sound :
(1) loudness
(2) pitch
(3) quality or timbre.
Ans.
(1) Loudness : The loudness of a note is the magnitude of the sensation produced by the sound waves on the ear. It depends upon
(a) the energy of the vibration
(b) the sensitiveness of the individual ear
(c) the pitch of the sound.
The loudness of a sound depends on the intensity of the sound wave, which is in turn proportional to the square of the amplitude of the wave itself. Loudness is a physiological (subjective) sensation, while intensity is an objectively measurable physical property of the wave. There is no direct relation between loudness and intensity. Near the middle of the audible range of frequencies, the ear is very sensitive to changes in intensity, which it interprets as changes in loudness.
The unit of loudness is the phon. It is equal to the loudness in decibel of any equally loud pure tone of frequency 1000 Hz.
(2) Pitch : By pitch we mean whether the note is high or low. The pitch of a note depends upon the frequency of the sound. But pitch is not determined by frequency alone. A physiological factor is involved and the sense of pitch is modified by the loudness and quality of the sound.
The average range of frequencies that the human ear detects as sound is approximately 20 Hz to 20000 Hz (the audible range). The human ear is capable of detecting a difference in pitch between two notes. The smallest difference in frequency that the ear can detect as a difference in pitch is approximately proportional to the frequency of one of the notes. That is, a given change in frequency of a low note will produce a greater change in pitch than it will in a high note.
(3) Quality : By quality or timbre is meant that characteristic of a sound by which it is possible to distinguish it from all other sounds of the same pitch and loudness. The same note played at the same loudness on two different musical instruments are easily distinguished from each other by their timbre.
[Note : A pure note, consisting of only one frequency, is different from a musical note, which may be a combination of many different frequencies. A musical note has a fundamental, or lowest frequency, and superimposed on it are higher frequencies, called overtones or partials. The number and relative strengths of the partials present determines the timbre of the note. The ear always recognizes the fundamental as determining the pitch of the note.]
Question 85.
Define intensity of sound. State its unit.
Answer:
Definition : The intensity of sound at a point is the time rate of flow of sound energy passing normally through a unit area at that point.
SI unit: the joule per second square metre (j/s.m2) or watt per square metre (W/m2).
Question 86.
What are the factors affecting the loudness of sound ? Is intensity the same as loudness ?
Answer:
(1) The factors affecting the loudness of sound are
- the amplitude of the vibrations of the body
- the distance of the listener from the vibrating body
- the surface area of the vibrating body
- the density of the medium
- the presence of the resonating bodies
- the sensitivity of the ear of the listener.
(2) Intensity and loudness are related, but not the same. Intensity is a measurable quantity whereas loudness is a sensation which is not measurable. Loudness depends on the intensity of sound as well as the sensitivity of the ear of the listener.
Question 87.
Explain the term decibel
Answer:
The intensity level of a sound wave, by definition, is β = log10 \(\left(\frac{I}{I_{0}}\right)\)bels = 10 log10 \(\left(\frac{I}{I_{0}}\right)\) decibels as one decibel is 0.1 bel. Here, I0 (reference intensity) is taken as 10-12 W/m2.
Intensity level is expressed in decibel (dB). There is no direct relation between loudness and intensity. The decibel is not a unit of loudness.
[Note : The decibel, equal to 0.1 bel, is used for comparing two power levels, currents or voltages. The unit bel is named in honour of Alexander Graham Bell (1847-1922) British-American scientist, inventor of the telephone (1876).]
Question 88.
What is the difference between a musical sound and a noise ?
Answer:
A musical sound is pleasing to the listener while a noise is not. The pleasure derived from a musical note is because it strikes the ear as a perfectly undisturbed, uniform sound which remains unaltered as long as it exists. On the other hand, noise is accompanied by a rapid, irregular but distinct, alternations of various kinds of sounds.
A musical sound thus has a regularity or smoothness because the vibrations that cause the sound are periodic. But the converse, that if the vibrations are regular the sound is musical, is not always true. For example, a ticking clock does not produce a musical note, or the definite note produced by a card held against the teeth of a rotating toothed wheel is far from being pleasant to hear. Bearing such reservations in mind, the essential difference between music and noise is that the former is produced by periodic and continuous vibrations, while noise results from discontinuous sudden and sharp sounds with no marked periodicity.
Question 89.
- Which quantity out of frequency and amplitude determines the pitch of the sound?
- Which out of pitch and frequency is a measurable quantity ?
Answer:
- The frequency of sound determines its pitch. A high pitched or shrill sound is produced by a body vibrating with a high frequency and a low pitched or flat sound is produced by a body vibrating with a low frequency.
- Frequency is a measurable quantity whereas pitch is not a measurable quantity.
Question 90.
Write a note on the major diatonic scale.
OR
Explain what is a musical scale.
Answer:
A musical scale is constructed on the basis of certain groups of notes with simple intervals. A major chord or triad is a group of three notes with frequencies in the ratio 4:5:6 that produce a very pleasing effect when sounded together. The diatonic musical scale is composed of three sets of triads making eight notes.
Some note called the tonic, is chosen as the basis of the scale, and a triad is constructed using this note as the one of lowest frequency. Calling the tonic as the 1st, the major chords are 1st, 3rd and 5th, 4th, 6th and 8th, and 5th, 7th and 9th; 8th and 9th are respectively the octaves of the 1st and 2nd.
In addition to the eight notes of an octave, that form the major scale, five additional notes are also used. These are derived either by raising or lowering the pitch by the interval 25 / 24. If the pitch is raised the note is sharp, and when lowered, it is flat.
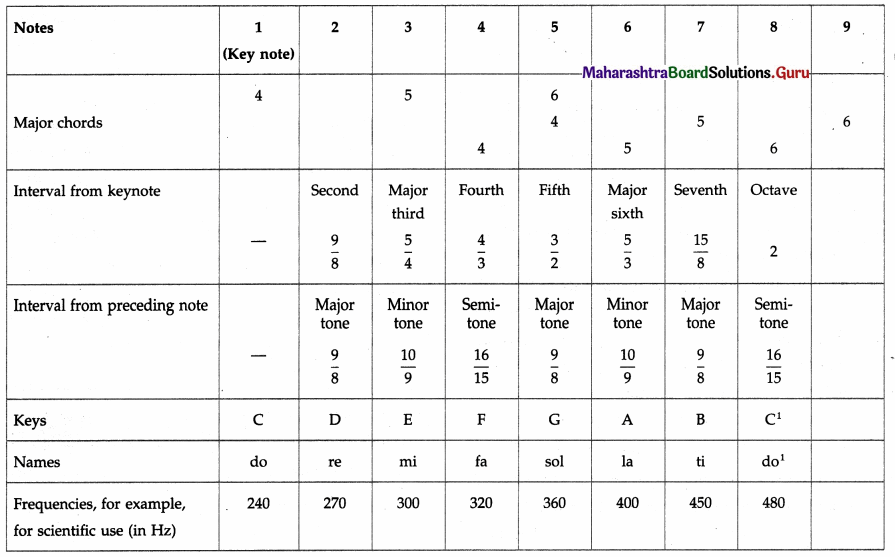
Question 91.
Write a short note on Indian musical scale.
Answer:
Indian music is chiefly based on melody, i.e., consonant notes in suitable succession. Besides this physiological sensation, there is a deep psychological involvement.
The notes or svaras (स्वर) used in an Indian musical scale have the same musical intervals as those of the major diatonic scale. The five additional notes in pure intonation, तीव्र (sharp) and कोमल (flat) are also used. Thus, the choice is usually made from the following twelve svaras : सा (shadja), रे(को) and रे (rishabha), ग(को) and ग g\(\bar{a}\)ndh\(\bar{a}\)ra), म and म(ती) (madhyam), प (pancham), ध (को) and ध (dhaivata), नी(को) and नी (nishad), सा. However, as compared to the fixed frequency of the tonic in western music, an Indian vocalist or musician has the freedom to set any frequency as the tonic. Besides, unlike western music, dissonant intervals are sometimes introduced to enhance the musical effect.
However, the whole structure of Indian music is based on r\(\bar{a}\)gas (राग), which are well-established melody types with a wide variety of emotional content. They can be courageous, amorous, melancholy, cheerful, soothing, or ecstatic. R\(\bar{a}\)gas are capable of conveying these emotions to the listener and different r\(\bar{a}\)gas are assigned to different seasons and different parts of the day.
Question 92.
Give reasons :
The notes of a sitar and a guitar sound different even if they have the same loudness and the pitch.
Answer:
The quality or timbre of the sound of a sitar is different from that of a guitar. The number of overtones or partials present and their relative intensities determine the quality or timbre of the sound of a musical instrument. Therefore, even if the pitch and the loudness are the same, the notes of a sitar and a guitar sound different.
Question 93.
Which are the three broad types of musical instruments ?
OR
Write a short note on types of musical instruments.
Musical instruments have been classified in various ways. One ancient system that was based on the primary vibrating medium distinguished three main types of instruments : stringed, wind and percussion.
Examples :
(1) Stringed instruments (stretched strings) :
(a) Plucked : Tanpura, sitar, veena, guitar, harp
(b) Bowed : Violin
(c) Struck : Santoor, pianoforte )
(2) Wind instruments :
(a) Free (air not confined) : Harmonica or mouth organ (without keyboard), harmonium (with keyboard). (Both are reed instruments in which free brass reeds are vibrated by air, blown or compressed.)
(b) Edge (air blown against an edge) : Flute
(c) Reedpipes : Saxophone (single reed), shehnai and bassoon (double reeds)
(3) Percussion instruments :
(a) Stretched skin heads : Tabla, mridangam, drums
(b) Metals (struck against each other or with a beater) : Cymbals, Xylophone
Question 94.
A simple harmonic wave of frequency 20 Hz is travelling in the positive direction of x-axis with a velocity of 30 m/s. Two particles in the path of the wave, 0.45 m apart, differ in phase by
(A) \(\frac{\pi}{3}\) rad
(B) \(\frac{\pi}{2}\) rad
(C) 0.6 π rad
(D) π rad.
Answer:
(C) 0.6 π rad
Question 95.
What is the period of the wave given by y = 0.003 sin (\(\frac{\pi}{0.08}\)t + \(\frac{\pi}{8}\)x ) (in SI units) ?
(A) 0.08 s
(B) 0.16 s
(C) 0.32 s
(D) 0.8 s.
Answer:
(B) 0.16 s
![]()
Question 96.
The equation of a progressive wave is y = 7 sin(4t – 0.02x), where x and y are in centimetre and time t in second. The maximum velocity of a particle is
(A) 28 cm/s
(B) 32 cm/s
(C) 49 cm/s
(D) 112 cm/s.
Answer:
(A) 28 cm/s
Question 97.
When a longitudinal wave is incident at the boundary of a denser medium, then
(A) a compression reflects as a compression
(B) a compression reflects as a rarefaction
(C) a rarefaction reflects as a compression
(D) a longitudinal wave reflects as a transverse wave.
Answer:
(A) a compression reflects as a compression
Question 98.
A transverse wave travelling in a denser medium is reflected from a rarer medium. Then,
(A) an incident crest is reflected as a crest
(B) an incident crest is reflected as a trough
(C) there is a phase change of 2π rad
(D) there is a phase change of π/2 rad.
Answer:
(A) an incident crest is reflected as a crest
Question 99.
Two simple harmonic waves of the same amplitude and frequency, but 90° out of phase, pass through the same region in a medium. The resultant wave has
(A) an amplitude greater than either of the component waves
(B) an amplitude smaller than either of the component waves
(C) zero amplitude
(D) an amplitude slowly varying with time.
Answer:
(A) an amplitude greater than either of the component waves
Question 100.
At a given instant two vibrating particles in the same loop of a stationary wave have
(A) the same phase
(B) opposite phases
(C) slightly different phases
(D) opposite velocities.
Answer:
(A) the same phase
Question 101.
Two vibrating particles in the adjacent loops of a stationary wave have ….. at a given instant.
(A) the same phase
(B) opposite phases
(C) slightly different phases
(D) the same velocity
Answer:
(B) opposite phases
Question 102.
A stretched string, 2 m long, vibrates in its third overtone. The distance between consecutive nodes is
(A) 40 cm
(B) 50 cm
(C) 66.7 cm
(D) 100 cm.
Answer:
(B) 50 cm
Question 103.
A stretched string of length l vibrates in the third overtone. The wavelength of stationary wave formed is
(A) \(\frac{l}{2}\)
(B) \(\frac{l}{4}\)
(C) l
(D) 21.
Answer:
(A) \(\frac{l}{2}\)
Question 104.
A stretched string tied between two rigid supports vibrates with a frequency double the fundamental frequency. The point midway between the supports is
(A) a node
(B) an antinode
(C) either a node or an antinode
(D) neither a node nor an antinode.
Answer:
(A) a node
Question 105.
A travelling wave of frequency 100 Hz along a string is reflected from a fixed end. The stationary wave formed has the nearest node at a distance of 10 cm from the fixed end. The speed of the travelling wave was
(A) 40 m/s
(B) 20 m/s
(C) 10 m/s
(D) 5m/s.
Answer:
(B) 20 m/s
Question 106.
Stationary waves are produced on a 10 m long stretched string fixed at both ends. If the string vibrates in 5 segments and the wave velocity is 20 m/s, the frequency of the waves is
(A) 10 Hz
(B) 5 Hz
(C) 4 Hz
(D) 2 Hz.
Answer:
(B) 5 Hz
Question 107.
The fundamental frequency of transverse vibrations of a stretched string of radius r is proportional to
(A) r-2
(B) r-1
(C) \(r^{-\frac{1}{2}}\)
(D) r2.
Answer:
(B) r-1
Question 108.
A stretched string of length 50 cm vibrates in five segments when stationary waves are formed on it. If the wave speed is 14 m/s, its frequency of vibration is
(A) 28 Hz
(B) 35 Hz
(C) 70 Hz
(D) 140 Hz.
Answer:
(C) 70 Hz
Question 109.
Two strings A and B are identical except that the diameter of A is twice the diameter of B. The ratio of the frequency of sound from A to that from B is
(A) 2 : 1
(B) \(\sqrt{2}\) : 1
(C) 1 : \(\sqrt{2}\)
(D) 1 : 2.
Answer:
(D) 1 : 2.
Question 110.
Two strings, A and B, have the same tension and length. The string A has a mass m while the string B has a mass Am. If the speed of the waves in string A is v, that on string B is
(A) \(\frac{1}{2}\)v
(B) v
(C) 2v
(D) v.
Answer:
(A) \(\frac{1}{2}\)v
Question 111.
An organ pipe is closed at one end. The pth overtone is the ….. th harmonic.
(A) 2p + 1
(B) 2p – 1
(C) p + 1
(D) P – 1
Answer:
(A) 2p + 1
Question 112.
Of two narrow organ pipes A and B, A is open at one end and B at both ends. Both the pipes have the same fundamental frequency. If A is 1.2 m long, how long is B?
(A) 0.8 m
(B) 1.8 m
(C) 2.4 m
(D) 3.0 m
Answer:
(C) 2.4 m
Question 113.
The value of end correction for an open organ pipe of radius r is
(A) 0.3 r
(B) 0.6 r
(C) 0.9 r
(D) 1.2 r.
Answer:
(D) 1.2 r.
Question 114.
Of two long narrow organ pipes A and B, A is open at one end and B at both ends. If both the pipes have the same fundamental frequency, the first overtone of A is ….. the first overtone of B.
(A) half of
(B) \(\frac{2}{3}\) of
(C) equal to
(D) twice
Answer:
(B) \(\frac{2}{3}\) of
Question 115.
In an open organ pipe, the first overtone produced is of such frequency that the length of the pipe is equal to
(A) \(\frac{\lambda}{4}\)
(B) \(\frac{\lambda}{3}\)
(C) \(\frac{\lambda}{2}\)
(D) λ
Answer:
(D) λ
Question 116.
A sonometer wire vibrates with three nodes and two antinodes. The corresponding mode of vibration is
(A) the first overtone
(B) the second overtone
(C) the third overtone
(D) the fourth overtone.
Answer:
(A) the first overtone
Question 117.
Velocity of a transverse wave along a stretched string is proportional to [T = tension in the string]
(A) \(\sqrt{T}\)
(B) T
(C) \(\frac{1}{\sqrt{T}}\)
(D) \(\frac{1}{T}\)
Answer:
(A) \(\sqrt{T}\)
Question 118.
The frequency of the second overtone of the vibration of a stretched string is
A. \(\frac{1}{l} \sqrt{\frac{T}{m}}\)
B. \(\frac{3}{2 l} \sqrt{\frac{T}{m}}\)
C. \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\)
D. \(\frac{2}{3 l} \sqrt{\frac{T}{m}}\)
Answer:
B. \(\frac{3}{2 l} \sqrt{\frac{T}{m}}\)
Question 119.
When the air column in a pipe closed at one end vibrates such that three nodes are formed in it, the frequency of its vibrations is ….. times the fundamental frequency.
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(D) 5
Question 120.
One beat means that the intensity of sound should be
(A) once maximum
(B) once minimum
(C) once maximum and once minimum
(D) twice maximum and twice minimum.
Answer:
(C) once maximum and once minimum
Question 121.
Let n1 and n2 be two slightly different frequencies of sound waves. The time interval between a waxing and the immediate next waning is
(A) \(\frac{1}{n_{1}-n_{2}}\)
(B) \(\frac{2}{n_{1}-n_{2}}\)
(C) \(\frac{n_{1}-n_{2}}{2}\)
(D) \(\frac{1}{2\left(n_{1}-n_{2}\right)}\)
Answer:
(D) \(\frac{1}{2\left(n_{1}-n_{2}\right)}\)
Question 122.
In the formation of beats, the resultant amplitude varies with a frequency equal to
(A) the beat frequency
(B) the average frequency
(C) half the beat frequency
(D) double the beat frequency.
Answer:
(C) half the beat frequency
Question 123.
A tuning fork A of frequency 512 Hz produces 3 beats per second with another tuning fork B of frequency 515 Hz. If the prongs of B are filed a little, the number of beats produced per second will
(A) increase
(B) decrease
(C) remain the same
(D) increase or decrease.
Answer:
(A) increase
Question 124.
A tuning fork gives 1 beat in 2 seconds with a timing fork of frequency 341.3 Hz. If the beat frequency decreases when the first fork is filed a little, its original frequency was
(A) 336.3 Hz
(B) 340.8 Hz
(C) 341.8 Hz
(D) 346.3 Hz.
Answer:
(B) 340.8 Hz
Question 125.
In a set of 25 tuning forks, arranged in order of increasing frequency, each fork gives 3 beats per second with the succeeding one. If the frequency of the 10th fork is 127 Hz, the frequency of the 16th fork is
(A) 139 Hz
(B) 145 Hz
(C) 148 Hz
(D) 151 Hz.
Answer:
(B) 145 Hz
![]()
Question 126.
If two sound waves with the same amplitude but slightly different frequencies n1 and n2 superpose to produce beats, the resultant wave motion has frequency
(A) |n1 – n2|
(B) n1 + n2
(C) \(\frac{\left|n_{1}-n_{2}\right|}{2}\)
(D) \(\frac{n_{1}+n_{2}}{2}\)
Answer:
(D) \(\frac{n_{1}+n_{2}}{2}\)