Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 11 Magnetic Materials Important Questions and Answers.
Maharashtra State Board 12th Physics Important Questions Chapter 11 Magnetic Materials
Question 1.
How did a magnet derive its name? What was its ancient use?
Answer:
The characteristic of a magnet to attract iron is called its attractive property. This property was discovered in a rock found in the ancient mineral-rich region of Magnesia (modern Turkey). The word magnet is derived from this Magnesian rock.
The rock when floated on water (by tying it to a piece of wood) or suspended freely was found to align approximately in the north-south direction. Because this directional property was used by some ancient travellers to locate the geographic north, it was also called the leading stone or lodestone.
The Magnesian rock is the naturally magnetized iron ore magnetite (Fe3O4). It is hard, black or brownish-black with a metallic luster.
Question 2.
Explain the directional characteristic of a bar magnet.
Answer:
When a bar magnet is suspended so as to rotate freely in a horizontal plane, it comes to rest in approximately the North-South direction.
The end of the magnet directed towards the Earth’s geographic North Pole is called the north-seeking pole or the north pole, and the other end which is directed towards the Earth’s geographic South Pole is called the south-seeking pole or the south pole.
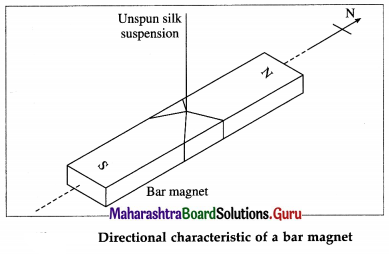
The cause for this alignment is seen when we consider the turning moment on a bar magnet suspended in a uniform magnetic induction \(\vec{B}\), as shown in below figure. The north pole (pole strength + m) and the south pole (pole strength – m) of the bar magnet experience equal and opposite forces of magnitude mB. If the lines of action of these two forces are not the same, they constitute a couple whose effect is to produce rotation.
![]()
Question 3.
State the expression for the torque acting on a magnetic dipole in a uniform magnetic field.
Answer:
When a magnetic dipole of magnetic dipole moment \(\vec{M}\) is placed in a uniform magnetic field of induction \(\vec{B}\), it experiences a torque whose magnitude is
τ = MB sin θ
where θ is the smaller angle between the magnetic axis and \(\vec{B}\).
[Note: When the dipole is placed with its axis at right-angles to the field, i.e, θ = 90°,
τ = MB or M = \(\frac{\tau}{B}\)
This is the defining equation for the magnetic dipole moment.]
Question 4.
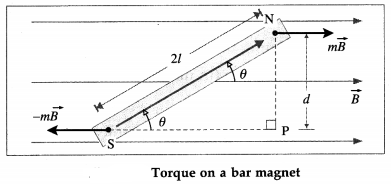
Derive an expression for the torque acting on a magnetic dipole placed in a region of uniform magnetic induction. Express it in vector form.
Answer:
Consider a magnetic dipole consisting of two point poles of pole strength m a distance 2l apart with its axis inclined at an angle θ to a uniform magnetic field of induction \(\vec{B}\), shown in figure. The magnetic force on the positive (or north) pole is m\(\vec{B}\), while that on the negative (or south) pole is – m\(\vec{B}\). These two forces, equal in magnitude, opposite in direction and separated by a finite distance, constitute a couple which tends to line up the magnetic dipole moment with the field \(\vec{B}\).
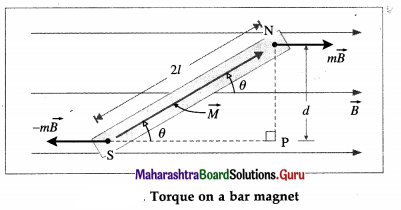
The torque of the couple in the clockwise sense in above figure in magnitude, is
τ = (mB) d
where d is the distance between the lines of action of the forces.
∴ τ = (mB)2lsin θ = MB sin θ (∵ m = \(\frac{M}{2 l}\))
Expressed as a vector product,
\(\vec{\tau}=\vec{M} \times \vec{B}\)
The torque has a maximum magnitude, (m2l)B, when sin θ = 1, i.e., when the magnet is perpendicular to the field. The torque vanishes when the magnet is parallel to the field, where sin θ = 0.
Question 5.
A current-carrying coil with magnetic moment \(\vec{M}\) (M = 5 A∙m2) is placed in a uniform magnetic field of induction \(\vec{B}\) (B = 0.2 Wb/m2) such that the angle between \(\vec{M}\) and \(\vec{B}\) is 30°. What is the torque acting on the coil ?
Answer:
τ = MB sin θ = (5) (0.2) sin 30° = 0.5 N∙m is the torque acting on the coil.
![]()
Question 6.
Explain what is meant by magnetic potential energy of a bar magnet kept in a uniform magnetic field. Discuss the cases when
(1) θ = 0°
(2) θ = 180°
(3) θ = 90°.
Answer:
A magnet free to rotate in a uniform magnetic field \(\vec{B}\) aligns its dipole moment \(\vec{M}\) with \(\vec{B}\). Work must be done to rotate the magnet from this equilibrium position. The work done is stored as the magnetic potential energy, also called its orientation energy. In a finite angular displacement from 0 to θ, the
magnetic potential energy
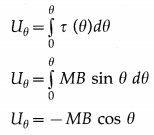
- When θ = 0°, cos θ = cos 0° = 1, Uθ = – MB. At this position, the magnetic moment of the bar magnet is lined up with the field and its magnetic potential energy is minimum. This is its most stable equilibrium position.
- When θ = 180°, cos θ = cos 180° = – 1, Uθ = MB. At this position, the magnetic moment is antiparallel to the field and its magnetic potential energy is maximum. This is its most unstable position.
- When θ = 90°, cos θ = cos 90° = 0, Uθ = 0. At this position, the bar magnet is perpendicular to the
magnetic field. Its magnetic potential energy is zero.
Question 7.
What is the nature of the graph between the magnetic potential energy of a bar magnet kept in a uniform magnetic field and angular position of the magnet ?
OR
Draw a graph of magnetic potential energy as a function of angular displacement.
Answer:
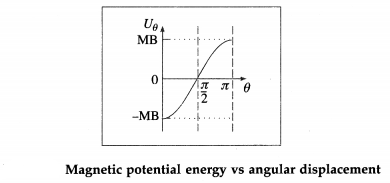
Question 8.
Derive the expression for the time period of angular oscillations of a bar magnet kept in a uniform magnetic field.
Answer:
Consider a bar magnet of magnetic dipole moment \(\vec{M}\), suspended by a light twistless fibre in a uniform magnetic field \(\vec{B}\) in such a way that it is free to rotate in a horizontal plane. In the rest position θ = 0, \(\vec{M}\) is parallel to \(\vec{B}\).
If magnet is given a small angular displacement θ from its rest position and released, the magnet performs angular or torsional oscillations about the rest position.
Let I be the moment of inertia of the bar magnet about the axis of oscillation and α the angular acceleration. The deflecting torque (in magnitude) is
τd = Iα = I \(\frac{d^{2} \theta}{d t^{2}}\) …………….. (1)
However, the restoring torque tries to bring back the oscillating bar magnet in the rest position. The restoring torque (in magnitude) is, τr = – MB sin θ …………. (2)
The minus sign in Eq. (2) indicates that restoring torque is opposite in direction to the angular deflection.
In equilibrium, both the torques balance each other. From Eqs. (1) and (2),

Eq. (4) represents angular simple harmonic motion.
Writing ω2 = \(\frac{M B}{I}\) , the angular frequency ω of the motion is
ω = \(\sqrt{\frac{M B}{I}}\) ………….. (5)
The time period of oscillations of the bar magnet is
T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{I}{M B}}\) ……………… (6)
This is the required expression.
9. Solve the following
Question 1.
Find the magnitude of the magnetic moment of a magnet if a couple exerting torque 0.5 N.m is required to hold the magnet with its axis perpendicular to a uniform magnetic field of induction 2 × 10-3 T.
Solution:
Data : τ = 0.5 N∙m, B = 2 × 10-3 T, θ = 90°
τ = MB sin θ
∴ M = \(\frac{\tau}{B \sin \theta}=\frac{0.5 \mathrm{~N} \cdot \mathrm{m}}{\left(2 \times 10^{-3} \mathrm{~T}\right) \sin 90^{\circ}}\)
= 250 A∙m2
The magnitude of the magnetic moment of the magnet is 250 A∙m2.
![]()
Question 2.
A magnetic dipole of magnetic moment 5 A∙m2 is placed in a uniform magnetic field of induction 10-3 T. Find the magnitude of the maximum torque acting on the dipole.
Solution:
Data : M = 5 A∙m2, B = 10-3 T
Torque, τ = MB sin θ
The magnitude of the torque is maximum when θ = 90°.
∴ τmax = MB = 5 × 10-3 N∙m
Question 3.
A bar magnet of magnetic length 0.12 m and pole strength 10 A-m is placed in a uniform magnetic field of induction 3 × 10-2 tesla. If the angle between the magnetic induction and the magnetic moment is 30°, find the magnitude of the torque acting on the magnet.
Solution:
Data : 2l = 0.12 m, m = 10 A∙m, B = 3 × 10-2 T,
θ = 30°
The magnitude of the torque,
τ = MB sin θ = m (2l) B sin θ
= (10 A∙m) (0.12 m)(3 × 10-2 T) sin 30°
= 3.6 × 10-2 × \(\frac{1}{2}\)
= 1.8 × 10-2 N∙m
Question 4.
A bar magnet of moment 10 A∙m is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 36 µT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 8C and magnetic potential energy.
Solution:
Data : M = 10 A∙m2, Bh = 36µT = 3.6 × 10-5 T,
θ = 8°
The magnitude of the torque is
τ = MBh sin θ
= (10) (3.6 × 10-5) sin 8°
= (36 × 10-5) (0.1391) = 5.007 × 10-5 N∙m
The magnetic potential energy of the bar magnet is
Uθ = MBh cos θ
= (36 × 10-5) cos 8°
= (36 × 10-5) (0.99) = 3.564 × 10-4 J
Question 5.
The time period of angular oscillation of a bar magnet in a horizontal magnetic field is 3.14 s. If the horizontal component of the Earth’s magnetic field at the place is 40 µT and the moment of inertia of the magnet is 10-4 kg∙m2, calculate the magnetic moment of the magnet.
Solution:
Data : T = 3.14 s, Bh = 40 µT = 4 × 10-5 T,
I = 10-4 kg∙m2

![]()
Question 6.
A bar magnet of moment 10 A∙m2 is suspended such that it can rotate freely in a horizontal plane. The horizontal component of the Earth’s magnetic field at the place is 36 µT. Calculate the magnitude of the torque when its angular displacement with respect to the direction of the field is 8° and magnetic potential energy.
Solution:
Data : M = 10 A∙m2, Bh = 36 µT = 3.6 × 10-5 T, θ = 8°
The magnitude of the torque is
τ = MBh sin θ
=(10)(3.6 × 10-5)sin8°
=(36 × 10-5)(0.1391) = 5.007 × 10-5 N∙m
The magnetic potential energy of the bar magnet is
Uθ = MBh cos θ
=(36 × 10-5)cos8°
=(36 × 10-5)(0.99) = 3.564 × 10-4 J
Question 10.
As the electron revolves in the second Bohr orbit in the hydrogen atom, the corresponding current is (about) 1.3 × 10-4 A. If the area of the orbit is (about) 1.4 × 10-19 m2, what is the (approximate) equivalent magnetic moment?
Answer:
M = IA = (1.3 × 10-4)(1.4 × 10-19)
= 1.82 × 10-23 A∙m2 is the (approximate) equivalent magnetic moment.
Question 11.
What is the magnetic moment of an electron due to its orbital motion?
Answer:
The orbital magnetic moment of an electron, of charge e and revolving with speed v in an orbit of radius r, is \(\frac{1}{2}\) evr.
Question 12.
If the frequency of revolution of a proton (q = 1.6 × 10-19 C) in a uniform magnetic induction is 106 Hz, what is the corresponding electric current?
Answer:
I = \(\frac{q}{T}\) = qf = (1.6 × 10-19)(106)
= 1.6 × 10-13 A
is the corresponding electric current.
Question 13.
The frequency of revolution of the electron in the second Bohr orbit in the hydrogen atom is 8.22 × 1014 Hz. What is the corresponding electric ’ current? [e = 1.6 × 10-19 C]
Answer:
I = \(\frac{e}{T}\) = ef
= (1.6 × 10-19)(8.22 × 1014)
= 1.315 × 10-4A
is the corresponding electric current.
![]()
Question 14.
A coil has 1000 turns, each of area 0.5 m2. What is the magnetic moment of the coil when it carries a current of 1 mA ?
Answer:
Magnetic moment M = NIA
= 1000 × 1 × 10-3 × 0.5
= 0.5 A∙m2
Question 15.
What is the gyromagnetic ratio of an orbital electron ? State its dimensions and the SI unit.
Answer:
The ratio of the magnitude of the orbital magnetic moment to that of the orbital angular momentum of an electron in an atom is called its gyromagnetic ratio γ0. If \(\vec{M}_{\mathrm{o}}\) is the orbital magnetic moment of the electron with orbital angular momentum \(\vec{L}_{\mathrm{o}}\),
γ0 = \(\frac{M_{\mathrm{o}}}{L_{\mathrm{o}}}=\frac{e}{2 m_{\mathrm{e}}}\)
where e and me are the electronic charge and electron mass, respectively.
Dimensions : [γ0] = \(\frac{[\text { charge }]}{[\text { mass }]}=\frac{[T I]}{[M]}\) = [M-1TI].
SI unit : The coulomb per kilogram (C/kg).
[Note : γ0 = 8.794 × 1010 C/kg. The gyromagnetic ratio of electron spin is nearly twice that of an orbital electron.]
16. Solve the following
Question 1.
A circular coil of 300 turns and diameter 14 cm carries a current of 15 A. What is the magnitude of the magnetic moment associated with the coil?
Solution :
Data : N = 300, d = 14 cm, I = 15 A
r = \(\frac{d}{2}\) = 7 cm = 7 × 10-2 m
The magnitude of the magnetic moment associated with the coil is
M = NIA = NI(πr2)
= (300)(15)(3.142)(7 × 10-2)2
= 4500 × 3.142 × 49 × 10-4
= 69.28 A∙m2
Question 2.
A coil has 300 turns, each of area 0.05 m2.
(i) Find the current through the coil for which the magnetic moment of the coil will be 4.5 A∙m2.
(ii) It is placed in a uniform magnetic field of induction 0.2 T with its magnetic moment making an angle of 30° with \(\vec{B}\). Calculate the magnitude of the torque experienced by the coil.
Solution:
Data : N = 300, A = 0.05 m2, M = 4.5 A∙m2, B = 0.2 T, θ = 30°
(i) M = NIA
∴ The current in the coil,
I = \(\frac{M}{N A}=\frac{4.5}{300 \times 0.05}\) = 0.3 A
(ii) The magnitude of the torque,
τ = MB sin θ = 4.5 × 0.2 × sin 30°
= 0.9 × \(\frac{1}{2}\) = 0.45 N∙m
![]()
Question 3.
An electron in an atom revolves around the nucleus in an orbit of radius 0.5 Å. Calculate the equivalent magnetic moment if the frequency of revolution of the electron is 1010 MHz.
Solution:
Data : r = 0.5 Å = 5 × 10-11 m,
f = 1010 MHz = 1016 Hz, e = 1.6 × 10-19 C
Equivalent current, I = \(\frac{e}{T}\) = ef
The equivalent magnetic moment is
M = IA = ef(πr2)
= (1.6 × 10-19)(1016)(3.142)(5 × 10-11)2
= 1.6 × 3.142 × 25 × 10-25
= 1.257 × 10-23 A∙m2
Question 4.
Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom. The radius of the orbit is 2.126 Å and the orbital speed of the electron in the orbit is 1.09 × 106 m/s.
Solution:
Data : r = 2.126 Å = 2.126 × 10-10 m,
v = 1.09 × 106 m/s, e = 1.6 × 10-19 C
The orbital magnetic dipole moment of the electron,
M0 = \(\frac{1}{2}\) evr
=(1.6 × 10-19)(1.09 × 106)(2.126 × 10-10)
=1.6 × 1.09 × 1.063 × 10-23
= 1.854 × 10-23 A∙m2
Question 5.
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Å. If the frequency of revolution of an electron is 9 × 109 MHz, calcu-late the orbital angular momentum. [Charge on an electron = 1.6 × 10-19 C, gyromagnetic ratio = 8.8 × 1010 C/kg, π = 3.142]
Solution:
Data : r = 0.53 Å = 0.53 × 10-10 m,
f = 9 × 109 MHz = 9 × 1015 Hz, e = 1.6 × 10-19 C, gyromagnetic ratio = 8.8 × 1010 C / kg, π = 3.142
Magnetic moment, M0 =IA = efπr2
= 1.6 × 10-19 × 9 × 1015 × 3.142 × (0.53 × 10-10)2
= 14.4 × 3.142 × (0.53)2 × 10-19 × 1015× 1020
= 1.272 × 10-23 A∙m2

Question 6.
The specific charge (charge-to-mass ratio) of an electron is 1.759 × 1011 C/kg.
(i) What is the gyromagnetic ratio of an orbital electron?
(ii) If the measured component of its orbital angular momentum is 2.11 × 10-34 kg∙m3/s. what Is the associatcd orbital magnetic dipole moment?
Solution:
Data: \(\frac{e}{m_{e}}\) = 1.759 × 1011 C/kg,
L = 2.11 × 10-34 kg∙m2/s
(i) The gyromag1etic ratio of an orbital electron,
γ0 = \(\frac{e}{2 m_{\mathrm{e}}}=\frac{1.759 \times 10^{11}}{2}\) =8.795 × 1010 C/kg
(ii) For the given component of the orbital angular momentum, the associated magnetic dipole moment is
Mo = \(\frac{e}{2m_{e}}\) L0 = γ0L0
= (8.795 × 1010 )(2.11 × 10-34)
= 1.856 × 10-23 A∙m2
![]()
Question 7.
An electron performs uniform circuLar motion in a uniform magnetic field of induction 1.2T In a plane perpendicular to the field. Its kinetic energy is 6 × 10-20 J and its motion is subject only to the magnetic force due to the field. What is the magnetic dipole moment associated with the motion of the electron?
Solution:
Data:B = 1.2T, KE ≡ Ek = 6 × 10-20 J
The centripetal force on the electron is the magnetic force. If r and e are respectively the radius of the path and linear speed of the electron,

Question 8.
If the magnetic moment of an electron revolving in an orbit of radius 0.4 Å is 9 × 10-24 A∙m2 then find the linear momentum of the electron in that orbit. (e/m = 1.76 × 1011 C/kg]
Solution:
Data: r = 0.5 Å = 5 × 10-11 m, I = 1.1 × 10-3 A,
x = 100 Å = 10-8 m, \(\frac{\mu_{0}}{4 \pi}\) = 10-7 T∙m/A
The magnitude of the magnetic induction at an axial point of a current loop,
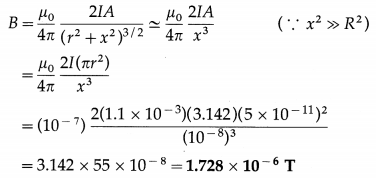
Question 9.
The magnetic moment of an electron revolving in a circular orbit of radius 2.2 Å is 5.024 × 10-24 A∙m2. Calculate the frequency of revolution of the electron in that orbit.
Solution:
Data: d = 0.2 m, B = 4 × 10-4 T,
2l = 5 cm = 5 × 10-2 m, A = 2 cm2 = 2 × 10-4 m2,
\(\frac{\mu_{0}}{4 \pi}\) = 10-7 T∙m/A
The magnitude of the magnetic induction at an axial point of a bar magnet.

Question 17.
Explain magnetization of a material.
Answer:
In an atom, the orbital and spin magnetic moments of its electrons may or may not add up to zero, depending on the electronic configuration. In some materials, their atoms have a net magnetic moment. When such a material is placed in an external magnetic field of induction \(\overrightarrow{B_{0}}\) , the field exerts a torque on each atomic magnet. These torques tend to align the magnetic moments with the applied field. Due to this, the material as a whole acquires a net magnetic moment \(\vec{M}_{\text {net }}\) along \(\overrightarrow{B_{0}}\) and the material is said to be magnetized.
The net magnetic moment per unit volume is called the magnetization \(\vec{M}_{z}\) of the material.
\(\vec{M}_{\mathrm{z}}=\vec{M}_{\text {net }} / V\)
where V is the volume of the material.
Even when the atomic magnetic moment is zero, application of magnetic field induces magnetism in the material. In this case, the magnetization has direction opposite to that of the applied field.
![]()
Question 18.
Define magnetization.
State its dimensions and the SI unit.
OR
Define magnetization. State its formula and SI unit.
Answer:
Magnetization : The net magnetic moment per unit volume of a material is called the magnetization of the material.

SI unit: The ampere per metre (A/m).
Question 19.
A bar magnet (volume 1.5 × 10-5 5m3) has a uniform magnetization of 6000 Aim. What is its magnetic dipole moment?
Answer:
Mz = \(\)
∴ M = MzV = (6000)(1.5 × 10-5)
= 9 × 10-2 A∙m2 is the magnetic dipole moment of the magnet.
Question 20.
Define magnetic intensity.
State its dimensions and the SI unit.
Answer:
Magnetic intensity: The magnetic intensity is defined as the magnetic induction in an isotropic medium divided by the permeability of the medium.
The magnetic intensity is a quantitative characteristic of a magnetic field independent of the magnetic properties of the medium. In a medium, it determines the contribution to the magnetic induction in the medium by the external magnetic field.
Dimensions: Within a toroid without a core, which has n windings per unit length carrying a current I, the magnetic intensity, H = nI.
∴ [H] = [n][I] = [L-1][I] = [L-1I]
SI unit : The ampere per metre (A/m).
[Note : The magnetic intensity (also called the magnetic field strength), \(\vec{H}\), is defined as
\(\vec{H}=\frac{\vec{B}}{\mu_{0}}-\overrightarrow{M_{z}}\)
where \(\vec{B}\) is the magnetic induction, \(\vec{M}_{z}\) is the magnetization and μ0 is the permeability of free space.]
![]()
Question 21.
What is the magnetic susceptibility of a medium?
Answer:
The magnetic susceptibility of a medium is a dimensionless quantity which signifies the contribution made by the medium when subjected to a magnetic field to the magnetic induction inside the medium. For a material in which the magnetization Mz is proportional to the magnetic intensity H, the magnetic susceptibility of the medium is
χm = Mz/H
It is equal to the fractional change in the magnetic induction due to the medium.
Magnetic susceptibility of some materials
| Substance | χ | Substance | χ |
| Silicon | -4.2 × 10-6 | Aluminium | 2.3 × 10-5 |
| Bismuth | -1.66 × 10-5 | Calcium | 1.9 × 10-5 |
| Copper | -9.8 × 10-6 | Choromium | 2.7 × 10-4 |
| Diamond | -2.2 × 10-5 | Lithium | 2.1 × 10-5 |
| Gold | -3.6 × 10-5 | Magnesium | 1.2 × 10-5 |
| Lead | -1.7 × 105 | Niobium | 2.6 × 10-5 |
| Mercury | -2.9 × 10-5 | Oxygen (STP) | 2.1 × 10-6 |
| Nitrogen | -5.0 × 10-9 | Platinum | 2.9 ×10-4 |
Question 22.
Discuss magnetization of a rod of material having net magnetic moment with the help of a solenoid.
OR
Discuss magnetization of an iron rod placed in a solenoid.
OR
Discuss magnetization of a magnetic material placed in a solenoid.
Answer:
Consider an ideal air-cored solenoid carrying a steady current I. The magnitude of the magnetic induction inside the solenoid is
B0 = \(\frac{\mu_{0} N I}{2 \pi r}\) = μonI ………….. (1)
where n = \(\frac{N}{2 \pi r}\) is the number of turns per unit length and p0 is the permeability of free space.
When a core of magnetic material (such as iron) is present, the magnetic field within the solenoid due to the current in the winding magnetizes the material of the core. With the core, the magnetic induction \(\vec{B}\) inside the solenoid is greater than \(\vec{B}_{0}\), so that
B = B0 + Bm ……………. (2)
where Bm is the contribution of the iron core. Bm is proportional to the magnetization Mz of the material.
Bm = μoMz …………… (3)
While discussing magnetic materials, it is customary to call \(\frac{B_{0}}{\mu_{0}}\) as the magnetizing field or magnetic field intensity, denoted by H, which produces the magnetization.
∴ B0 = μoH …………. (4)
Substituting for B0 and BM in Eq. (1),
B = μ0H + μ0Mz = μ0(H + Mz) …………….. (5)
For materials in which the magnetization is pro-portional to the magnetic intensity,
Mz ∝ H or Mz = χmH ………. (6)
where the constant of proportionality χm is called the magnetic susceptibility.
∴ B = μ0(H + χmH) = μ0(1 + χm)H = μH …………. (7)
where p = μ0(1 + χm) is called the permeability of the material.
[Notes : (1) Mz ∝ H only for diamagnetic and paramagnetic materials. Among ferromagnetic materials, the linear relation in Eq. (6) holds good only for initial magnetization of magnetically softer materials; for magnetically harder materials, Mz is not a single-valued function of H, and depends on the magnetic intensity that the material has been previously exposed to (a phenomenon known as hysteresis). (2) H is defined for convenience; B is more fundamental.]
Question 23.
What is the relation between permeability and magnetic susceptibility of a medium? What is relative permeability of a medium ?
Answer:
If χm is the magnetic susceptibility of a medium, the permeability of the medium is
μ = μ0 (1 + χm)
where μ0 is the permeability of free space.
The ratio of the permeability of a medium to that of free space is called the relative permeability of the medium, denoted by μr.
μr = μ/μ0 = 1 + χm
Question 24.
Write the relation between relative permeability and magnetic susceptibility.
Answer:
μr = 1 – χm, where μr is the relative permeability and χm is the magnetic susceptibility of a substance.
![]()
Question 25.
Why do magnetic lines of force prefer to pass through iron than air?
Answer:
The permeability of air (≅ 1.00000037) is negligible relative to that of iron, which typically has μ of several hundreds or thousands. That is, permeability of iron is much more than that of air. Hence, magnetic lines of force prefer to pass through iron than air.
[Note : Air is paramagnetic due to the oxygen it contains. Reference for μair: B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, p. 16.]
Question 26.
Is magnetic susceptibility a dimensionless quantity? Why?
Answer:
In a magnetizing field of intensity H, a material for which its magnetization Mz ∝ H, we write . Mz = χmH, where the proportionality constant χm is called the magnetic susceptibility. Since both magnetization and magnetic intensity have the same dimensions and units, χm is a dimensionless quantity.
OR
The relative permeability of a medium,
μr = \(\frac{\mu}{\mu_{0}}\) = 1 + χm
where μ and χm are the permeability and magnetic susceptibility of the medium and μ0 is the permeability of free space. Hence, both μ0 and χm are dimensionless quantities.
27. Solve the following
Question 1.
A cylindrical magnet 5 cm long has a diameter of 1 cm and a uniform magnetization of 5000 A/m. Find its magnetic dipole moment.
Solution:
Data : L = 5 × 10-2 m, d = 1 × 10-2 m,
Mz = 5 × 103 A/m .
Volume, V = πr2L = \(\frac{\pi d^{2}}{4}\) L
Mz = \(\frac{M}{V}\)
∴ The magnetic dipole moment,
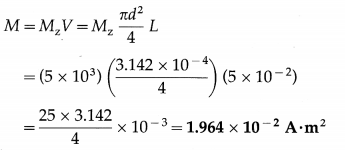
Question 2.
A bar magnet made of steel has magnetic moment 2.5 A∙m2 and mass 6.6 × 10-3 kg. Given that the density of steel is 7.9 × 103 kg/m3, find the intensity of magnetization of the magnet. (2 marks )
Solution:
Data : M = 2.5 A∙m2, m = 6.6 × 10-3 kg, ρ = 7.9 × 103 kg/m3
Volume, V = \(\frac{m}{\rho}\)
The intensity of magnetization of the magnet is
Mz = \(\) = M ∙ \(\frac{\rho}{m}\)
= 2.5 x \(\frac{M}{V}\) = 2.992 × 106 A/m
[Note : Intensity of magnetization = magnetization.]
Question 3.
Find the magnetization of a bar magnet of length 10 cm and cross-sectional area 4 cm2, if the magnetic moment is 2 A∙m2.
Solution:
Data : L = 0.1 m, A = 4 × 10-4 m2, M = 2 A∙m2
Magnetization, Mz = \(\frac{M}{V}\)
= \(\frac{M}{L A}=\frac{2}{(0.1)\left(4 \times 10^{-4}\right)}\)
= \(\frac{10^{4}}{0.2}\) = 5 × 104 A/m
Question 4.
The magnetic susceptibility of annealed iron at saturation is 5500. Find the permeability of annealed iron at saturation.
Solution:
Data : χm = 5500, μ0 = 4π × 10-7 T∙m/A
Permeability, μ = μ0(1 + χm)
The permeability of annealed iron at saturation is
μ = (4 × 3.142 × 10-7) (1 + 5500)
= 4 × 3.142 × 5.501 × 10-4
= 6.914 × 10-3 T∙m/A
![]()
Question 5.
The magnetic induction B and the magnetic intensity H in a material are found to be 1.6 T and 1000 A/m, respectively. Calculate the relative permeability μr and the magnetic susceptibility χm of the material.
Solution:
Data : B = 1.6 T, H = 1000 A/m,
μ0 = 4π × 10-7 T∙m/A
(i) B = μH = μ0μr H
∴ The relative permeability of the material,
μr = \(\frac{B}{\mu_{0} H}=\frac{1.6}{\left(4 \times 3.142 \times 10^{-7}\right)\left(10^{3}\right)}\)
= \(\frac{4000}{3.142}\) = 1.273 × 103
(ii) μr = 1 + χm
∴ The magnetic susceptibility of the material,
χm = μr – 1
= 1273 – 1 = 1272 or 1.272 × 103
Question 6.
An ideal solenoid has a core of relative permeability 500 and its winding has 1000 turns per metre. If a steady current of 1.6 A is passed through its winding, find
(i) the magnetic field strength H
(ii) the magnetization Mz
(iii) the magnetic induction B within the solenoid. Assume that Mz is directly proportional to H and single valued.
Solution:
Data : μr = 500, n = 1000 m-1, I = 1.6 A,
μ0 = 4π × 10-7 T∙m/A
(i) The magnetic field strength (or magnetic intensity) of the ideal solenoid,
H = nI
= 1000 × 1.6 = 1.6 × 103 A/m
(ii) The magnetization of the core,
Mz = χmH = (μr – 1)H
= (500 – 1) × 1.6 × 103
= 499 × 1.6 × 103 = 7.984 × 105 A/m
(iii) The magnetic induction within the core of the solenoid,
B = μrμ0H
= (500) (4 × 3.142 × 10-7) (1.6 × 103)
= 32 × 3.142 × 10-2 = 1.005 T
Question 28.
What is a diamagnetic material? Give two examples.
Answer:
A material which is weakly repelled by a magnet and whose atoms /molecules do not possess a net magnetic’ moment in the absence of an external magnetic field is called a diamagnetic material.
When a diamagnetic material is placed in a uniform magnetic field, it acquires a small net induced magnetic moment directed opposite to the field.
Examples: Bismuth, copper, gold, silver, anti-mony, mercury, water, air, hydrogen, lead, silicon, nitrogen, sodium chloride.
Question 29.
What is diamagnetism?
Answer:
A material which is weakly repelled by a magnet and whose atoms/molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material. When a diamagnetic material is placed in a mag-netic field, it acquires a small net induced magnetic moment directed opposite to the field. The induced magnetism exhibited by such materials is called diamagnetism.
![]()
Question 30.
State any four properties of a diamagnetic material.
Answer:
Properties of a diamagnetic material :
- In the absence of an external magnetic field, the magnetic dipole moment of each atom / molecule of a diamagnetic material is zero.
- A diamagnetic material is weakly repelled by a magnet.
- If a thin rod of a diamagnetic material is suspended in a uniform magnetic field, it comes to rest with its length perpendicular to the field.
- When placed in a nonuniform magnetic field, a diamagnetic material is repelled from the region of strong field.
- The magnetic susceptibility (χm) of a diamagnetic material is small and negative.
- χm is very nearly temperature-independent.
- The relative permeability (μr) of a diamagnetic material is slightly less than 1 and very nearly temperature independent.
- If a diamagnetic liquid in a watch glass is placed on two closely spaced pole-pieces of a magnet, the liquid accumulates on the sides causing a depression at the centre.
[ Note : When the pole-pieces are moved apart, the effect is reversed, i.e., the diamagnetic liquid accumulates at the centre, where the magnetic field is weak.] - A diamagnetic liquid in a U-tube placed in a magnetic field shows a depression in the arm to which the magnetic field is applied.
- If a diamagnetic gas is introduced between the pole-pieces of a magnet, it spreads at right angles to the field.
Question 31.
Name two materials that have negative magnetic susceptibility.
Answer:
Copper and gold have negative magnetic susceptibility.
Question 32.
Explain the origin of diamagnetism.
OR
Explain the origin of diamagnetism on the basis of atomic structure.
Answer:
An atomic electron is equivalent to a current loop which has orbital magnetic moment. Further, electron spin gives rise to the spin magnetic moment. The magnetic moment of an atom is equal to the vector sum of the magnetic moments of all its electrons.
The electronic configuration in an atom of a diamagnetic material is such that the vector sum of the orbital and spin magnetic moments of all the electrons is zero. Thus, the atomic magnetic moment is zero. Hence, a diamagnetic material has no inherent magnetic moment associated with it.
When a diamagnetic material is placed in a magnetic field, the orbiting electrons are accelerated or decelerated depending on their sense of revolution. For the electrons that are speeded up, the magnetic moment increases and for those that are slowed down, the magnetic moment decreases. This happens due to induced current as per Lenz’s law. Thus, each atom acquires a net magnetic moment and the diamagnetic material is weakly magnetized. The induced magnetic moment is opposite in direction to the applied field.
Diamagnetism is the weakest magnetic phenomenon. Hence, although diamagnetism is a universal property, it can be detected only in the absence of properties resulting in para- and ferromagnetism.
![]()
Question 33.
Explain the diamagnetic behaviour of superconductors.
Answer:
Suppose a superconducting material in its normal phase, not the superconducting phase, is placed in a uniform applied magnetic field of induction \(\vec{B}\) which is weaker than a certain critical magnetic induction \(\vec{B}_{\mathrm{c}}\) for that material. Then, when the temperature is reduced below the critical temperature for the material, it enters into the superconducting phase and the magnetic field is expelled from the interior of the material.
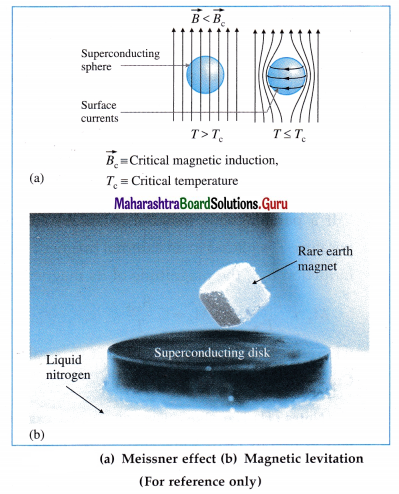
There is no magnetic field inside the material, i.e., the material exhibits perfect diamagnetism. The expulsion of the magnetic field in a superconducting material is called the Meissner effect.
[Notes : (1) What happens is that currents appear on the surface of the material whose magnetic field exactly cancels the applied field inside it. (2) The German physicists Fritz Walther Meissner (1882-1974) and Robert Ochsenfeld (1901-1993) discovered the phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin and lead samples. The Meissner effect is so strong that a magnet can actually be levitated over a material cooled below its superconducting transition temperature Tc.]
Question 34.
What is a paramagnetic material? Give two examples.
Answer:
A material which is weakly attracted by a magnet and whose atoms possess a net magnetic moment with all atomic magnetic moments randomly directed in the absence of an external magnetic field but are capable of being aligned in the direction of the applied magnetic field is called a paramagnetic material.
Examples : Aluminium, platinum, chromium, manganese, sodium, calcium, magnesium, lithium, tungsten, niobium, copper chloride, oxygen.
Question 35.
State any four properties of a paramagnetic material.
Answer:
Properties of a paramagnetic material:
- Each atom of a paramagnetic material possesses a magnetic dipole moment. However, in the absence of an external magnetic field, the atomic magnetic moments are randomly oriented and hence the resultant magnetization of a paramagnetic material is zero.
- A paramagnetic material is weakly attracted by a magnet.
- If a thin rod of a paramagnetic material is sus-pended in a uniform magnetic field, it comes to rest with its length parallel to the field.
- When placed in a nonuniform magnetic field, a paramagnetic material is attracted towards the region of strong field.
- The magnetic susceptibility (χm) of a paramagnetic material is small and positive.
- χm varies inversely with the absolute temperature T.
- The relative permeability (μr) of a paramagnetic material is slightly greater than 1 and decreases with increasing temperature.
- If a paramagnetic liquid in a watch glass is placed on two closely spaced pole-pieces of a magnet, it shows a slight rise in the middle.
[Note : If the pole-pieces are moved apart, the para-magnetic liquid moves away from the centre where the field is weak and gets depressed in the middle.] - A paramagnetic liquid in a U-tube placed in a magnetic field shows a rise in the arm to which the magnetic field is applied.
Question 36.
Give one example each of a diamagnetic material and a paramagnetic material.
Answer:
Bismuth is a diamagnetic material and aluminium is a paramagnetic material.
![]()
Question 37.
Name two materials that have small and positive magnetic susceptibility.
Answer:
Platinum and Chromium have small and positive magnetic susceptibility.
Question 38.
The relative permeability of two materials are 0.999 and 1.001. Identify the materials.
Answer:
A material with relative permeability μr ≤ 1 is diamagnetic while the one with μr ≥ 1 is paramagnetic.
Question 39.
Explain the origin of paramagnetism.
OR
Explain the origin of paramagnetism on the basis of atomic structure.
Answer:
Paramagnetism depends on the presence of permanent atomic or molecular magnetic dipole moments. The inherent net atomic magnetic mo-ment results from a particular combination of the spin and orbital magnetic moments of its electrons.
The spin magnetic moments of the electrons in matter are affected by the internal magnetic field created by the magnetic moments of surrounding electrons. This internal field, ~ 10-2 T to 10-1 T,
causes the spin magnetic moments to precess about the field direction. At normal temperature; the thermal motion of the electrons produces constant fluctuations in the internal field so that the spin magnetic moments have random directions, from figure (a). In the absence of an external magnetizing field, therefore, a paramagnetic material is not magnetized.
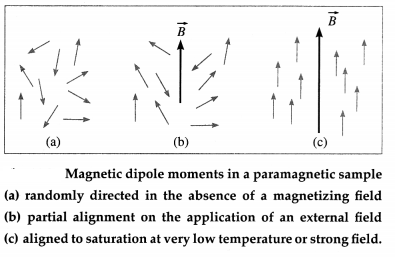
When the applied field strength is greater than that of the internal field, the spin magnetic moments tend to align parallel to the external field direction. But the randomizing effect of thermal agitation prevents complete alignment, from figure (b). Therefore, at room temperature, when a paramagnetic material is placed in a magnetic field, it is weakly magnetized in the direction of the magnetizing field.
If the external field is very large or the temperature is very low, the magnetic dipole moments are effectively aligned parallel to the field so as to have the least magnetic potential energy and the magnetization reaches saturation, from figure (c).
![]()
Question 40.
Discuss Curie’s law for paramagnetic material.
OR
State Curie’s law of paramagnetism.
Answer:
Curie’s law : The magnetization of a paramagnetic material is directly proportional to the external magnetic field and inversely proportional to the absolute temperature of the material.
If a paramagnetic material at an absolute temperature T is placed in an external magnetic field of induction \(\overrightarrow{B_{\text {ext }}}\), the magnitude of its magnetization
Mz ∝ \(\frac{B_{\text {ext }}}{T}\) ∴ Mz = C \(\frac{B_{\text {ext }}}{T}\)
where the proportionality constant C is called the Curie constant.
[Notes : (1) The above law, discovered experimentally in 1895 by Pierre Curie (1859-1906) French physicist, is true only for values of Bext/ T below about 0.5 tesla per kelvin.
(2) [C] = [Mz ∙ T] / [Bext] = [L-1I∙![]() ] /[MT-2I-1]
] /[MT-2I-1]
= [M-1L-1T2I2![]() ],
],
where ![]() denotes the dimension of temperature.]
denotes the dimension of temperature.]
Question 41.
Prove that the magnetic susceptibility of a para-magnetic material is inversely proportional to its absolute temperature.
Answer:
Consider a paramagnetic material at an absolute temperature T placed in an external magnetic field of induction \(\vec{B}_{\text {ext }}\). The magnitude of its magnetization is
Mz = C \(\frac{\vec{B}_{\text {ext }}}{T}\) …………. (1)
where the proportionality constant C is called the Curie constant.
Substituting \(\vec{B}_{\text {ext }}\) = μ0H in Eq. (1),
Mz = C \(\frac{\mu_{0} H}{T}\)
where µ0 is the permeability of free space and H is the intensity of the magnetizing field.
The magnetic susceptibility of the medium
χm = \(\frac{M_{z}}{H}\). Thus, Eq. (2) becomes ti
χm = C \(\frac{\mu_{0}}{T}\)
χm ∝ \(\frac{1}{T}\)
This is the required expression.
Question 42.
What is a ferromagnetic material? Give two examples.
Answer:
A material which is strongly attracted by a magnet and whose atoms possess a net magnetic moment (largely due to electron spin) which, within a certain temperature range, spontaneously line up parallel to each other by quantum mechanical exchange interaction is called a ferromagnetic material.
Examples : Transition elements (iron, cobalt and nickel), inner transition elements (gadolinium, Gd, and dysprosium, Dy) and their alloys.
[Note : Ferromagnetic behaviour was first explained by Pierre-Ernest Weiss on the basis of domain theory but its satisfactory explanation is given only by quantum mechanics.]
![]()
Question 43.
What are domains in a ferromagnetic material ?
OR
Write a short note on domains in a ferromagnetic material.
Answer:
A ferromagnetic material is composed of mosaic of small regions within each of which all the atomic magnetic moments spontaneously line up parallel to each other by quantum mechanical exchange interaction within a certain temperature range. Each such spontaneously magnetized region is called a domain and the common direction of magnetic moment is called the domain axis. A domain is an extremely small region (e.g., a size of about 10-6 m -10-4 m) containing a large number (1010 – 1017) of atoms. The boundary between adjacent domains with a different orientation of magnetic moment is called a domain wall.
Question 44.
Explain ferromagnetism on the basis of the domain theory.
Answer:
Atoms of a ferromagnetic material have a perms tient non-zero magnetic dipole moment arising mainly from spin magnetic moments of the electrons.
According to the domain theory, a ferromagnetic material is composed of small regions called domains.
A domain is an extremely small region contain Inga large number (something like 1015 atoms as in common iron) of atoms,
Within each domain, the atomic magnetic moments of nearest-neighbour atoms interact strongly through exchange interaction (a quantum mechanical phenomenon) and align themselves parallel to each other even in the absence of an extemal magnetic field. A domain is. therefore, spontaneously magnetized to saturation.
In an unmagnetized material, however, the directions of magnetization of the different domains are w oriented that the net magnetization is zero.
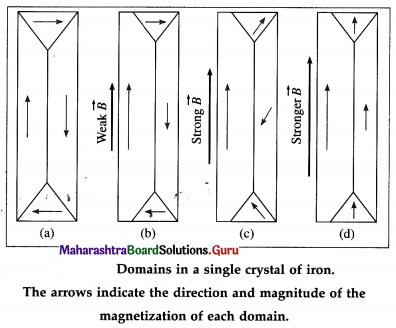
When an external magnetic field Is applied, the resultant magnetization of the specimen Increases. This is achieved in either of two ways: Either a domain that is favourably oriented grows in size at the expenses of a less favourably oriented domain, or the direction of magnetization of an entire domain changes and aligns along the external magnetic field.
When a weak nagnetic field is applied, favour ably oriented domains grow in size by domain boundary displacement, from figure (b). In strong fields, the domains change their magnetization by domain rotation, from figures. 11.9 (c) and (d). If domains reach perfect alignment, as in from figure 11.9 (d),, the domains may merge into one large domain.
After the external field is removed, it may be energetically favourable for a domain’s direction of magnetizaLion to persist. Then, the specimen has a permanent magnetic dipole moment. This phonomenon, called magnetic remanance, Is the basis of the existence of permanent magnets.
Question 45.
State any four properties of a ferromagnetic material.
Answer:
(1) Each atom of a ferromagnetic material possesses a magnetic moment. A ferromagnetic material is composed of domains each of which is spontaneously magnetized to saturation. In an unmagnetized sample, the magnetic moments of different domains are so oriented that the macroscopic magnetization of the sample is zero.
(2) When a ferromagnetic material is placed in a strong external magnetic field, the domains whose magnetic moments are favourably oriented relative to the external field grow in size such that the sample acquires a nonzero macroscopic magnetization.
(3) A ferromagnetic material retains some magnetization even after it is removed from an external magnetic field. This magnetic retentivity is the basis ‘ of the existence of permanent magnets.
(4) A ferromagnetic material is strongly attracted by a magnet.
(5) A bar magnet, suspended in a uniform magnetic field, comes to rest with its magnetic dipole moment in the direction of the external field.
(6) When placed in a nonuniform magnetic field, a ferromagnetic material is attracted towards the region of strong field.
(7) The magnetic susceptibility (χm) and relative permeability (μr) of a ferromagnetic material are very high.
![]()
Question 46.
Are the (i) diamagnetic materials (ii) paramagnetic materials (iii) ferromagnetic materials attracted or repelled by a magnet?
Answer:
When placed in a nonuniform magnetic field,
- a diamagnetic material is weakly repelled from’ the region of strong field
- a paramagnetic material is weakly attracted towards the region of strong field
- a ferromagnetic material is strongly attracted towards the region of strong field.
Question 47.
Can there be a material which is nonmagnetic?
Answer:
All materials are magnetic. However, only ferromagnetics can have magnetic remanance and exhibit magnetic behaviour even in the absence of an external magnetic field. Diamagnetics and para-magnetics exhibit induced magnetism, i.e., they exhibit magnetic behaviour only in the presence of an external magnetic field.
[Note : A solid solution formed between paramagnetic or diamagnetic metals can be an exception to the general statement that all substances are magnetic. However, the zero value of the susceptibility will be retained only at one temperature, because the susceptibility of the paramagnetic constituent generally changes with temperature. A Cu-Ni alloy with 3.7 wt% Ni has zero susceptibility at room temperature.]
Question 48.
Which magnetic materials have
(i) relative permeability > 1
(ii) relative permeability <1?
Answer:
(i) Both paramagnetic and ferromagnetic materials have relative permeability (μr) greater than 1. μr is only slightly greater than 1 for a paramagnetic material. μr is very high for a ferromagnetic material and is a function of the magnetizing field (also called the magnetic field intensity).
(ii) μr is slightly less than 1 for a diamagnetic material.
Question 49.
Draw a graph showing the variation of magnetic susceptibility of a ferromagnetic material with temperature.
Answer:
The magnetic susceptibility of a ferromagnetic material above Curie temperature Tc is given by χm = \(\frac{C}{T-T_{\mathrm{c}}}\), where C is the Curie constant. Below figure shows the variation of magnetic susceptibility of a ferromagnetic material with temperature.
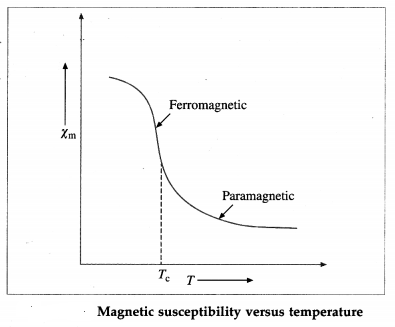
[Note : The relation, χm = \(\frac{C}{T-T_{\mathrm{c}}}\), is known as Curie-Weiss law. A plot of reciprocal susceptibility versus temperature for a ferromagnetic material is a straight line intercepting the temperature axis at T. At T = T, the susceptibility diverges which implies that one may have a nonzero magnetization in a zero applied field. This exactly corresponds to the definition of the Curie temperature, being the upper limit for having a spontaneous magnetization.].
![]()
Question 50.
Distinguish between a diamagnetic material and a paramagnetic material.
Answer:
| Diamagnetic material | Paramagnetic material |
| 1. A material whose atoms/ 1. molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material. | 1. A material whose atoms possess net magnetic moments that are all randomly directed in the absence of an external magnetic field is called a paramagnetic material. |
| 2. When placed in a nonuniform magnetic field, a diamagnetic material is weakly repelled from the region of strong field. | 2. When placed in a nonuniform magnetic field, a paramagnetic material is weakly attracted towards the region of strong field. |
| 3. In an external magnetic j field, it gets weakly magnetized in the direction opposite to that of the field. | 3. In an external magnetic field, it gets weakly magnetized in the same direction as that of the field. |
| 4. When a rod of a diamagnetic material is suspended in a uniform magnetic field, it comes to rest with its length perpendicular to the direction of the field. | 4. When a rod of a paramagnetic material is suspended in a uniform magnetic field, it comes to rest with its length parallel to the direction of the field. |
| 5. χm is small, negative and very nearly temperature independent. | 5. χm is small, positive and varies inversely with absolute temperature T |
| 6. μr is slightly less than 1 and very nearly temperature! independent. | 6. μr is slightly greater than 1 and decreases with increasing temperature. |
Question 51.
Distinguish between a paramagnetic material and a ferromagnetic material.
Answer:
| A paramagnetic material | A ferromagnetic material |
| 1. The permanent atomic magnetic moments of a paramagnetic material are all randomly oriented so that, in the absence of an external magnetizing field, the material is unmagnetized. |
1. The permanent atomic magnetic moments of a ferromagnetic material interact strongly through exchange interaction forming domains which are spontaneously magnetized to saturation |
| 2. It gets weakly magnetized when placed in an external magnetic field. | 2. In an unmagnetized material, the directions of magnetization of the different domains are so oriented that the net magnetization is zero. |
| 3. Its magnetization becomes zero when the external magnetic field is removed. | 3. It retains some magnetization even after the external magnetic field is removed. |
| 4. Its magnetization in a given external magnetic field increases with decreasing temperature. The magnetization reaches saturation only if the external field is very large and the temperature is very low. | 4. It retains its domain structure only up to a characteristic Curie temperature, above which it becomes paramagnetic. |
| 5. χm is small and positive. μr is slightly greater than 1. | 5. χm and μr are positive and very high. |
![]()
Question 52.
Distinguish between a ferromagnetic material and a diamagnetic material.
Answer:
| A ferromagnetic material | A diamagnetic material |
| 1. A material whose atoms/molecules possess permanent magnetic moments which interact strongly through exchange interaction to form magnetic domains, each of which is magnetized to saturation, is called a ferromagnetic material. | 1. A material whose atoms/molecules do not possess a net magnetic moment in the absence of an external magnetic field is called a diamagnetic material. |
| 2. It gets strongly magnetized in the direction of the field even when placed in a weak magnetic field | 2. In an external magnetic field, it gets weakly magnetized in the direction opposite to the field. |
| 3. It retains some magnetization even after the external magnetic field is removed. | 3. Its magnetization becomes zero when the external magnetic field is removed. |
| 4. When placed in a nonuniform magnetic field, a ferromagnetic material is strongly attracted towards the region of strong field. | 4. When placed in a nonuniform magnetic field, a diamagnetic material is weakly repelled from the region of strong field. |
| 5. χm and μr are positive and very high. | 5. χm is small and negative. μr is slightly less than 1. |
53. Solve the following
Question 1.
(5) A toroid (Rowland ring) of mean radius 16 cm has 1000 turns of wire closely wound on a ferromagnetic core of relative permeability 400. What is the magnetic induction B within the core for a magnetizing current of 1 A?
Solution:
Data: r = 16 × 10-2 m, N = 1000, μr = 400, I = 1 A,
μ0 = 4π × 10-7 T∙m/A
Magnetic field strength, H = nI = \(\frac{N I}{2 \pi r}\)
∴ The magnetic induction within the core,
B = μ0μrH = μ0μr \(\frac{N I}{2 \pi r}\)
= (4π × 10-7) (400) \(\frac{1000 \times 1}{2 \pi \times 16 \times 10^{-2}}\)
= \(\frac{8 \times 10^{-2}}{16 \times 10^{-2}}\) = 0.5 T
Question 2.
Find the percentage increase in the magnetic induction B when the space within a current-carrying toroid is filled with aluminium. The magnetic susceptibility of aluminium is 2.1 × 10-5.
Solution:
Data: χm = 2.1 × 10-5 (positive, since aluminium is paramagnetic)
The percentage increase in the magnetic induction B within the toroid due to the aluminium core

![]()
Question 3.
The permeability of a substance at temperature 300 K is 6.284 × 10-3 SI unit. At what temperature will the susceptibility of that substance increase to 9.998 × 103?
Solution:
Data: T1 = 300 K, μ1 = 6.284 × 10-3, χm2 = 9.998 × 103, μ0 = 4π × 10-7 T∙m/A
Permeability, μ = μ0(1 + χm)
∴ The magnetic susceptibility at temperature T1,

∴ The required temperature,
T2 = \(\frac{\chi_{\mathrm{m} 1}}{\chi_{\mathrm{m} 2}}\) × T1 = \(\frac{4999}{9998}\) × 300 = 150 K
Question 54.
Explain magnetic hysteresis in a ferromagnetic material.
OR
Explain the behaviour of a ferromagnetic material in an external magnetic field with the help of a magnetic hysteresis cycle.
OR
Explain the behaviour of a ferromagnetic material through one cycle of magnetization.
Answer:
A large scale consequence of the magnetic behaviour of a ferromagnetic under different applied magnetic fields can be observed by placing an unmagnetized rod of the material inside a solenoid. A current through the coil establishes the magnetizing field H, which we take as the independent variable. By measuring the voltage induced in a test coil wound alongside, we can determine changes in flux Φ, and hence changes in B inside the rod. B is measured in tesla while H is measured in ampere per metre. Knowing B and H, we can always compute magnetization M. It is however usual to plot B rather than M, as a function of H.
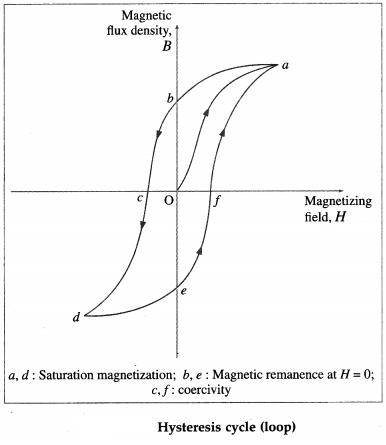
Typical B-H plot during the following operations :
(1) Starting with an unmagnetized rod, B = 0 and H = 0 (Point O), H is increased until it has the value corresponding to point a : Here the rod has reached its saturation magnetization and B remains constant even with further increase in H. The lower part of the curve Oa is governed by domain growth while the upper flattening part is governed by domain rotation.
(2) Reduce H to zero (point b) : the curve does not retrace itself, as shown by the curve ab. This irre-versibility is called hysteresis. It is largely due to the domain boundary movements being partially irreversible. If the current is simply switched off at this point, the rod will have a residual magnetization as indicated by the non-zero value of B, called retentivity or remanence, for H = 0. Essentially now B = μ0M, i.e., the rod has acquired a permanent magnetization.
(3) Reverse H and increase it in magnitude until it has the value corresponding to point c : Here B is zero. The corresponding reverse magnetizing field H is called coercivity.
(4) Increase H in reverse direction until saturation magnetization is reached (point d).
(5) Reduce H to zero again (point e).
(6) Reverse the current once more until point a is reached again.
The process of taking the magnetic material once through the hysteresis loop abcdefa is called hysteresis cycle.
Question 55.
What is magnetic hysteresis ?
Explain it on the basis of magnetic domains.
Answer:
Magnetic hysteresis is a phenomenon shown by ferromagnetic materials in which the magnetic flux density through a material depends on the applied magnetizing field as well as the previous state of magnetization. Due to retention of its memory of previous state of magnetization, the flux density B lags behind (does not remain in step) with magnetizing field H. This delay in the change of its magnetization M (or equivalently, B) in response to a change in H is called hysteresis.
Hysteresis can be understood through the concept of magnetic domains. Domain boundary displacements and domain rotations are not totally reversible. When the applied magnetizing field H is increased and then decreased back to its initial value, the domains do not return completely to their original configuration but retain some memory or history of their previous alignment.
![]()
Question 56.
Define :
(1) retentivity
(2) coercivity.
Answer:
- Retentivity : The residual magnetic flux density or magnetization in a magnetic material when the magnetizing field intensity is reduced to zero is called retentivity or remanence.
- Coercivity: The reversed magnetizing field strength required to reduce the remanent magnetic flux density or magnetization in a magnetic material from its remanent value to zero, i.e., to demagnetize the magnetic material completely, is
Question 57.
What is a ‘soft’ magnetic material?
OR
What is meant by a ‘soft’ iron?
Answer:
A soft magnetic material, usually iron-based, has high permeability, low retentivity and low coercivity. In other words, it does not have appreciable hysteresis, i.e., its hysteresis loop is very narrow. Such a material magnetizes and demagnetizes more easily, by small external fields.
Question 58.
What is an electromagnet?
Answer:
An electromagnet is an insulated coil wrapped around a ferromagnetic core (usually a soft iron) of high permeability and low retentivity. When a current is passed through the coil-a solenoid or toroid, the ferromagnetic material magnifies the magnetic field of the coil, the magnification factor being the relative permeability (μ / μ0) of the core. The magnetic field of the current-carrying coil magnetizes the core material, thereby producing a much larger field than the coil would produce by itself.
Question 59.
What is a magnetically hard material?
Answer:
A ‘hard’ magnetic material, such as ALNICO (an alloy of aluminium, nickel and cobalt), has high permeability, high retentivity and very high coercivity- of the orders of 1 tesla and 104 ampere per metre, respectively. In other words, it has a large zero-field magnetization, and large reverse field needed to demagnetize. Its hysteresis loop is very broad. Such a material can be made into a permanent magnet, that is, its magnetization will persist indefinitely if it is subsequently exposed only to weak magnetic fields.
![]()
Question 60.
Distinguish between an electromagnet and a permanent magnet.
Answer:
|
Electromagnet |
Permanent magnet |
| 1. Magnetic field of an electromagnet is retained till there is passage of electric current through the solenoid or coil. | 1. Magnetic field is retained for a long period of time. |
| 2. current through the solenoid and the number of turns per unit length of the solenoid. | 2. The strength of a permanent magnet depends upon the nature of the material of which it is made. |
| 3. For a good electromagnet, the retentivity and coercivity of the material should be low. | 3. For a good permanent mag net, the retentivity and coercivity of the material should be high. |
| 4. It is usually made of soft ferromagnetic material. | 4. It is usually made of hard ferromagnetic material. |
| 5. Poles of an electromagnet can be reversed by reversing the direction of electric current. | 5. Poles of a permanent magnet cannot be reversed. |
Question 61.
Explain magnetic shielding.
Answer:
The use of a shell or box of magnetic material of high permeability to protect sensitive instruments from stray magnetic fields is called magnetic shielding. The permeability of the material being many order of magnitudes greater than air, the magnetic field lines pass through the shell. The saturation v induction B of the material must be greater than the external field to be shielded. from below figure shows the cross section of a cylindrical or spherical shield in which the central region is the field-free region.
Magnetic shielding is useful for a wide range of applications, from small components inside a set of speakers to large magnetically shielded rooms.
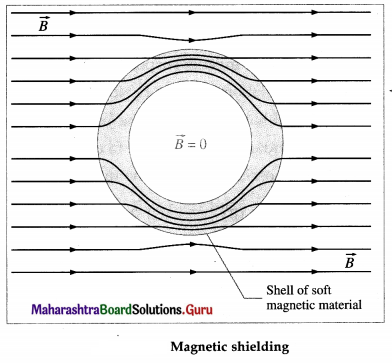
[Note : The most widely used alloy for magnetic shielding purposes is the patented MuMetal®. Its composition of 80% nickel, 4.5% molybdenum and balance iron gives it high permeability.] .
Multiple Choice Questions
Question 1.
A rectangular bar magnet-with sides l. b and w – h.is mass n and magnetic moment M. It is free to rotate about a vertical axis through its centre of mass such that its faces of area l × b are honzoritaL The period T of angular oscillations of this magnet in a uniform magnetic field B is given by
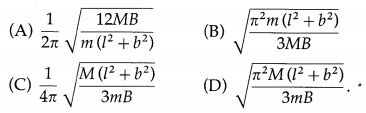
Answer:
(B) \(\sqrt{\frac{\pi^{2} m\left(l^{2}+b^{2}\right)}{3 M B}}\)
Question 2.
A magnet of moment \(\vec{m}\) is placed in a uniform magnetic field \(\vec{B}\). Which of the following graphs correctly depicts the variation of its orientation energy Uθ i.e., its potential energy due to its orientation θ with \(\vec{B}\)?
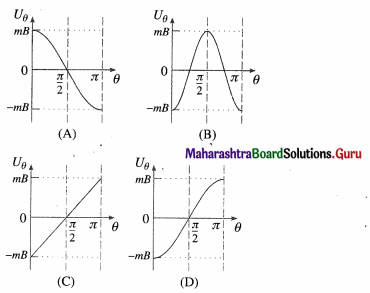
Answer:
(D)
Question 3.
The magnetic dipole moment has the dimensions of current
(A) \(\frac{\text { current }}{\text { area }}\)
(B) current × area
(C) \(\frac{\text { area }}{\text { current }}\)
(D) current × length.
Answer:
(B) current × area
Question 4.
The dimensions of magnetic dipole moment are
(A) [L2I]
(B) [LI]
(C) [L-1I]
(D) [L-2I]
Answer:
(A) [L2I]
Question 5.
The gyromagnetic ratio of an orbital electron is the ratio of its
(A) charge to mass
(B) magnetic moment to volume
(C) orbital magnetic moment to linear momentum
(D) orbital magnetic moment to orbital angular momentum.
Answer:
(D) orbital magnetic moment to orbital angular momentum.
![]()
Question 6.
If \(\vec{M}_{0}, \vec{L}_{0}\) and γ0 are respectively the magnetic dipole moment, orbital angular momentum and gyrornagnetlc ratio of an orbital electron. Then.
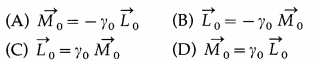
Answer:
(A) \(\vec{M}_{0}=-\gamma_{0} \overrightarrow{L_{0}}\)
Question 7.
Bohr magneton is the magnetic dipole moment of
(A) an orbital electron in the ground state of a Bohr atom
(B) an orbital electron with orbital angular momenturn of \(\frac{h}{2 \pi}\)
(C) the order of 10-23 J/T
(D) all of the above.
Answer:
(D) all of the above.
Question 8.
A bar magnet 10 cm long has cross-sectional area 2 cm2 and magnetic dipole moment of 10 A∙m2. The magnetization of its material, assumed to be uniform, is
(A) 5 × 105 A/m
(B) 2 × 105 A/m
(C) 0.5 A/m
(D) 0.2 A/m.
Answer:
(A) 5 × 105 A/m
Question 9.
An iron rod of volume 10-4 m3 acquires a magnetic moment of 25 A∙m2 when placed inside a solenoid whose windings carry a current of 0.5 A. The magnetization of the rod (in A/m), assumed to be uniform, is
(A) 5 × 10-5
(B) 2.5 × 10-3
(C) 12.5
(D) 2.5 × 105
Answer:
(D) 2.5 × 105
Question 10.
The dimensions of magnetic intensity are
(A) [LI]
(B) [L2I]
(C) [L-1I]
(D) [L-2I].
Answer:
(C) [L-1I]
Question 11.
The ratio of magnetization to magnetic field induction (M/B) for both diamagnetic and paramagnetic materials is, in the usual notation,
(A) χm
(B) \(\frac{\chi_{\mathrm{m}}}{\mu_{0}}\)
(C) µr
(D) µ
Answer:
(B) \(\frac{\chi_{\mathrm{m}}}{\mu_{0}}\)
![]()
Question 12.
Magnetic susceptibility for vacuum (where there is no matter) is
(A) zero
(B) positive
(C) negative
(D) infinite.
Answer:
(A) zero
Question 13.
Magnetic susceptibility is positive and small for
(A) silver
(B) platinum
(C) mercury
(D) sodium chloride.
Answer:
(B) platinum
Question 14.
The magnetic induction within an ideal solenoid with air core is 5 mT. With an iron core of magnetic susceptibility 500, the induction within changes by
(A) 2.5 T
(B) 25 T
(C) 50 T
(D) 100 T.
Answer:
(A) 2.5 T
Question 15.
The magnetic moment of any atom in an isolated diamagnetic material is
(A) zero
(B) small
(C) large
(D) negative.
Answer:
(A) zero
Question 16.
Which of the following is diamagnetic?
(A) Dysprosium
(B) Gadolinium
(C) Magnesium
(D) Silver
Answer:
(D) Silver
![]()
Question 17.
The most exotic diamagnetic materials are
(A) the glasses
(B) the insulators
(C) the superconductors
(D) the semiconductors.
Answer:
(C) the superconductors
Question 18.
A thin, small gIas rod is suspended between the poles of a strung electromagnet. The rod
(A) is strongly repelled by the magnetic field.
(B) orients itself parallel to the magnetic field
(C) orients itself perpendicuLar to the magnetic field
(D) is weakly attracted by the magnetic field
Answer:
(C) orients itself perpendicuLar to the magnetic field
Question 19.
Which of the following is paramagnetic?
(A) Bismuth
(B) Copper
(C) Liq. oxygen
(D) Silver
Answer:
(C) Liq. oxygen
Question 20.
When a parainagnetic material Is placed in a uniform magnetic field,
(A) its atoms acquire a magnetic moment opposite to the magnetic field
(B) the atomic magnetic moments tend to align along the magnetizing field
(C) all the atomic magnetic moments align along the magnetizing field
(D) the sample temporarily becomes ferromagnetic.
Answer:
(B) the atomic magnetic moments tend to align along the magnetizing field
Question 21.
Curte constant is
(A) a universal constant
(B) constant for a given paramagnetic material
(C) constant for a given diamagnetic material
(D) inversely proportional to the absolute temperature
Answer:
(B) constant for a given paramagnetic material
![]()
Question 22.
The rare-earth element, gadolinium, is
(A) diamagnetic
(B) paramagnetic
(C) ferromagnetic
(D) nonmagnetic.
Answer:
(C) ferromagnetic
Question 23.
Curie’s law is valid for
(A) diamagnelics
(B) paramagnetics
(C) ferromagnetics
(D) all materials,
Answer:
(B) paramagnetics
Question 24.
Magnetizing and demagnetizing a material that has hysteresis involves
(A) increase in the temperature of the material
(B) a terro-to-para phase change
(C) decrease in the temperature of the material
(D) none of the above.
Answer:
(A) increase in the temperature of the material
Question 25.
The length of a bar magnet is large compared to its width and breadth. The time period of its angular oscillation in a vibration magnetometer is 2s. The magnet is cut along its length into two equal parts and the two parts are then mounted together in the magnetometer with their like poles together. The time period of this combination will be
(A) 2 s
(B) 1 s
(C) \(\frac{1}{2}\) s
(D) \(\frac{1}{\sqrt{2}}\) s
Answer:
(B) 1 s