Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 4 Structure of Atom Important Questions and Answers.
Maharashtra State Board 11th Chemistry Important Questions Chapter 4 Structure of Atom
Question 1.
Complete the information about the properties of subatomic particles in the following table:
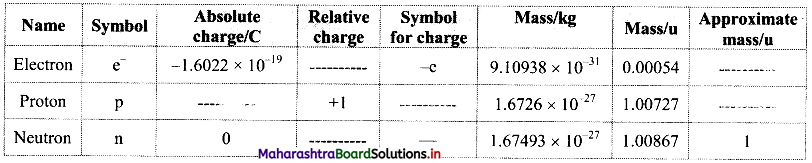
Answer:
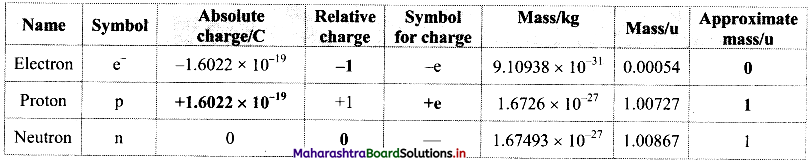
Question 2.
What are three important subatomic particles of an atom?
Answer:
Electron, proton and neutron are the three important subatomic particles of an atom.
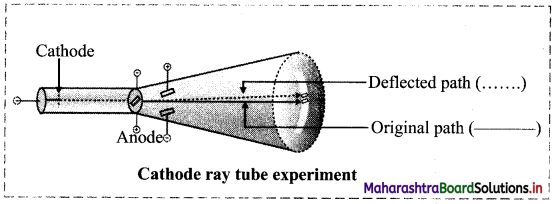
Question 3.
Write a short note on discovery of electron.
Answer:
- In the year 1897, J J. Thomson studied the properties of cathode rays through a cathode ray tube experiment and found that the cathode rays are a stream of very small, negatively charged particles.
- These particles are 1837 times lighter than a hydrogen atom and are present in all atoms.
- These particles were later named as electrons.
Question 4.
Draw labelled diagram of Rutherford’s α-particle scattering experiment.
Answer:
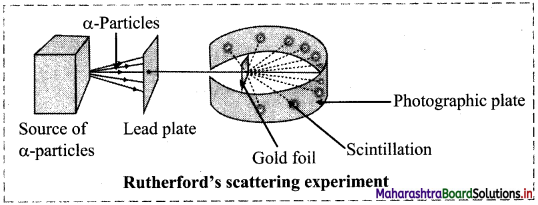
Question 5.
Write a short note on discovery of proton.
Answer:
- After the discovery of nucleus in an atom, Rutherford found that the fast moving α-particles transmuted nitrogen into oxygen with simultaneous liberation of hydrogen.
\({ }_{7}^{14} \mathrm{~N}+{ }_{2}^{4} \alpha \longrightarrow{ }_{8}^{17} \mathrm{O}+{ }_{1}^{1} \mathrm{H}\) - He further showed that other elements could also be transmuted similarly and hydrogen was always emitted in the process.
- Based on these observations, he proposed that the hydrogen nucleus must be contained inside nuclei of all the elements. Hence, he renamed hydrogen nucleus as proton.
![]()
Question 6.
Write a short note on discovery of neutron.
Answer:
- In 1920, Ernest Rutherford proposed the existence of an electrically neutral and massive particle in the nucleus of an atom in order to account for the disparity in atomic number and atomic mass of an element.
- In 1932, James Chadwick measured the velocity of protons ejected from paraffin by an unidentified radiation from beryllium (Be).
- From that he determined the mass of the particles of this unidentified neutral radiation, which was found to be almost same as that of the mass of a proton.
- He named this neutral particle as ‘neutron’, which was earlier predicted by Rutherford.
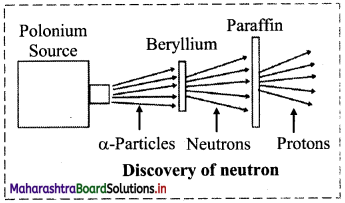
Question 7.
State true or false. Correct the false statement.
i. An electron is 1837 times lighter than a proton.
ii. In Rutherford’s experiment of scattering of α-particles by thin gold foil, most of the α-particles
bounced back.
iii. Cathode rays are a stream of very small, positively charged particles.
Answer:
i. True
ii. False,
In Rutherford’s experiment of scattering of α-particles by thin gold foil, very few α-particles bounced back.
iii. False,
Cathode rays are a stream of very small, negatively charged particles.
Question 8.
Explain the term: Atomic number
Answer:
- Atomic number is defined as the number of protons present in the nucleus of an atom of a particular element.
- Atomic number is represented by Z.
- An atom is electrically neutral. Hence, the number of protons equals to the number of electrons. In other words, the atomic number of an atom is equal to the number of electrons.
∴ Atomic Number (Z) = Number of protons = Number of electrons
Question 9.
Give reason: The approximate atomic mass in Daltons is numerically equal to the number of nucleons in the atom.
Answer:
- The electrons possess negligible mass. They do not contribute much to the mass of an atom.
- Therefore, the entire mass of an atom is supposed to be present in the nucleus which consists of protons and neutrons, which are collectively called as nucleons.
Hence, approximate atomic mass in Daltons is numerically equal to the number of nucleons in the atom.
![]()
Question 10.
Explain: Atomic mass number.
Answer:
- The sum of the total number of protons and neutrons present in the nucleus of an atom is called the atomic mass number of that atom.
- Atomic mass number is represented by A
- Mass number (A) = Number of protons (Z) + Number of neutrons (N) = Total number of nucleons
∴ A = Z + N OR N = A – Z
Question 11.
How is an atom of an element ‘X’ having atomic number ‘Z’ and atomic mass number ‘A’ represented?
Answer:
An atom of an element ‘X’ having atomic number ‘Z’ and atomic mass number ‘A’ is represented as: \({ }_{Z}^{A} X\)
Question 12.
What is a nuclide?
Answer:
The atom or nucleus having a unique composition as specified by \({ }_{Z}^{A} X\) is called as a nuclide.
Question 13.
If an element ‘X’ has 6 protons and 8 neutrons, then write its representation.
Answer:
The representation of the given element is \({ }_{6}^{14} \mathrm{X}\).
Question 14.
Three elements Q, R and T have mass number 40. Their atoms contain 22, 21 and 20 neutrons respectively. Represent their atomic composition with appropriate symbol.
Answer:
Mass number (A) = Number of protons (Z) + Number of neutrons (N) .
A = Z + N
∴ Z = A – N
For the given three elements, A = 40. Values of their atomic numbers Z, are calculated from the given values of the number of neutrons, N, using the above formula.
For Q: Z = A – N = 40 – 22 = 18
For R: Z = A – N = 40 – 21 = 19
For T: Z = A – N = 40 – 20 = 20
Now, atomic composition of an element (X) is represented as \({ }_{Z}^{A} X\).
The atomic compositions of the three elements are written as follows:
\({ }_{18}^{40} \mathrm{Q}\), \({ }_{19}^{40} \mathrm{R}\), \({ }_{20}^{40} \mathrm{T}\)
![]()
Question 15.
Find out the number of protons, electrons and neutrons in the nuclide \({ }_{18}^{40} \mathrm{Ar}\).
Solution:
For the given nuclide,
Atomic number, Z = 18, Mass number, A = 40
Number of protons = Number of electrons = Z = 18
Number of neutrons (N) = A – Z = 40 – 18 = 22
Ans: Number of protons = 18, Number of electrons = 18, Number of neutrons = 22
Question 16.
How many protons, electrons and neutrons are there in the following nuclei?
i. \({ }_{8}^{17} \mathrm{O}\)
ii. \({ }_{12}^{25} \mathrm{Mg}\)
iii. \({ }_{35}^{80} \mathrm{Br}\)
Solution:
i. \({ }_{8}^{17} \mathrm{O}\)
Atomic number, Z = 8, Mass number, A = 17
Number of protons = Number of electrons = Z = 8
Number of neutrons (N) = A – Z = 17 – 8 = 9
Ans: Number of protons = 8, Number of electrons = 8, Number of neutrons = 9
ii. \({ }_{12}^{25} \mathrm{Mg}\)
Atomic number, Z = 12, Mass number, A = 25
Number of protons = Number of electrons = Z = 12
Number of neutrons (N) = A – Z = 25 – 12 = 13
Ans: Number of protons = 12, Number of electrons = 12, Number of neutrons = 13
iii. \({ }_{35}^{80} \mathrm{Br}\)
Atomic number, Z = 35, Mass number, A = 80
Number of protons = Number of electrons = Z = 35
Number of neutrons (N) = A – Z = 80 – 35 = 45
Ans: Number of protons = 35, Number of electrons = 35, Number of neutrons = 45
Question 17.
Define isotopes.
Answer:
Isotopes are defined as the atoms of an element having the same number ofprotons but different number of neutrons in their nuclei.
e.g. \({ }_{6}^{12} \mathrm{C}\), \({ }_{6}^{13} \mathrm{C}\) and \({ }_{6}^{14} \mathrm{Br}\) are isotopes.
Question 18.
Complete the information about the isotopes of carbon in the following table:

Answer:

Question 19.
Define isobars.
Answer:
Isobars are defined as the atoms of different elements having the same mass number but different atomic number.
e.g. \({ }_{6}^{14} \mathrm{C}\) and \({ }_{7}^{14} \mathrm{N}\) are isobars.
![]()
Question 20.
Complete the following table:

Answer:

Question 21.
The two natural isotopes of chlorine viz. \({ }_{17}^{35} \mathrm{Cl}\) and \({ }_{17}^{37} \mathrm{Cl}\) exist in relative abundance of 3 : 1. Find out the average atomic mass of chlorine.
Solution:
Given: Isotopes of chlorine \({ }_{17}^{35} \mathrm{Cl}\) and \({ }_{17}^{37} \mathrm{Cl}\).
Ratio of relative abundance of these isotopes is 3 : 1.
To find: Average atomic mass of chlorine
Calculation: From the relative abundance 3 : 1, it is understood that out of 4 chlorine atoms, 3 atoms have mass 35 and 1 atom has mass 37.
Therefore, the average atomic mass of chlorine = \(\frac{3 \times 35+1 \times 37}{4}\) = 35.5
∴ Average atomic mass of chlorine = 35.5 u
Ans: The average atomic mass of chlorine is 35.5 u.
Question 22.
Find out the average atomic mass of lithium (Li) from the following data:
| Isotope | Atomic mass (u) | Abundance |
| 6Li | 6.015 | 7.59% |
| 7Li | 7.016 | 92.41% |
Solution:
Given: Three isotopes of lithium along with respective atomic mass and % abundance.
To find: Average atomic mass of lithium
Calculation:
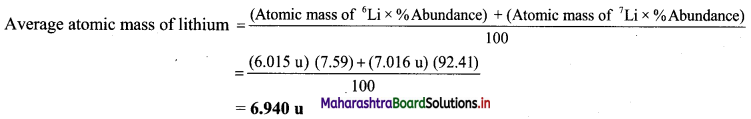
Ans: Average atomic mass of lithium is 6.940 u.
Question 23.
Certain results were obtained when scientists studied the interactions of radiation with matter. What were the two results, utilized by Neils Bohr to overcome the drawbacks of Rutherford model?
Answer:
The two results utilized by Neils Bohr to overcome the drawbacks of Rutherford model were:
- Wave particle duality of electromagnetic radiation
- Line emission spectra of hydrogen
![]()
Question 24.
Explain in short the wave particle duality of light (electromagnetic radiation).
Answer:
Wave particle duality of light (electromagnetic radiation):
- Light has both particle and wave like nature.
Phenomena such as diffraction and interference of light could be explained by treating light as electromagnetic wave. - However, the black-body radiation or photoelectric effect could not be explained by wave nature of light. This could be accounted for by considering particle nature of light. Thus, both phenomena could be explained only by accepting that light has dual behaviour.
- When light interacts with matter it behaves as a stream of particles (called photons) and when light propagates, it behaves as an electromagnetic wave.
Question 25.
Observe the following figure of an electromagnetic wave and answer the questions given below:
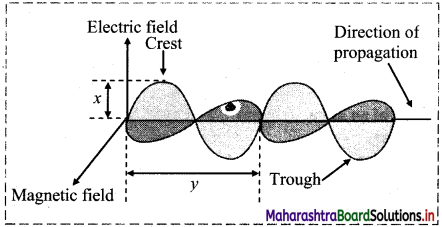
i. What does ‘x’ represent?
ii. What does ‘y’ represent?
Answer:
i. ‘x’ represents amplitude of the wave.
ii. ‘y’ represents wavelength of the wave.
Question 26.
Define and explain the following terms:
i. Wavelength (λ).
ii. Frequency (ν)
iii. Wavenumber (\(\bar{v}\))
iv. Amplitude (A)
v. Velocity (c)
Answer:
i. Wavelength (λ):
- The distance between two consecutive crests or two consecutive troughs in a wave is called wavelength.
- It is represented by Greek letter λ (lambda).
- The SI unit for wavelength is metre (m).
Note: The other units include Angstrom, nanometre, picometer (1 pm = 10-12 m) and micron (1µ = 10-6 m).
1Å = 10-8 cm = 10-10 m
1nm = 10-9 m = 10Å
ii. Frequency (ν):
- The number of waves that pass a given point in one second is called frequency.
- It is represented by Greek letter ‘ν’ (nu).
- The SI unit of frequency is Hertz (Hz) or s-1.
Note: 1 Hz = 1 cycle per second (1 cps)
The units, kilo Hertz (kHz) and mega Hertz (mHz) are commonly used.
1 kHz = 103 Hz = 103 cps
1 mHz = 106 Hz = 106 cps
iii. Wavenumber (\(\bar{v}\)):
- The number of wavelengths per unit length is called the wavenumber.
- It is represented by \(\bar{v}\) (nu bar).
- The commonly used unit for wavenumber is cm-1 while its SI unit is m-1.
- Wavenumber of a wave is related to the wavelength as follows:
\(\bar{v}\) = \(\frac{1}{\lambda}\)
iv. Amplitude (A):
- The height of a crest or the depth of a trough from the line of propagation of the wave is called
amplitude. - It is represented by letter ‘A’.
- The square of the amplitude represents the intensity (brightness) of the radiation.
v. Velocity (c):
- The distance travelled by a wave in one second is called the velocity of the wave.
- It is denoted by letter c.
- It is the product of the frequency and wavelength. Hence, c = νλ
- The velocity of all types of electromagnetic radiations (in space or in vacuum) is the same and it is equal to the velocity of light (3 × 1010 cm s-1 or 3 × 108 m s-1. However, they may have different wavelengths and frequencies.
Question 27.
Write a short note on quantum theory of radiation.
Answer:
i. Max Planck put forward a theory known as Planck’s quantum theory to explain black-body radiation.
ii. According to this theory, the energy of electromagnetic radiation depends upon the frequency and not the amplitude.
iii. The smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation is called as ‘quantum’.
iv. The energy (E) of each quantum of radiation is directly proportional to its frequency (ν).
i.e., E ∝ ν ; E = hν
where, h = Planck’s constant = 6.626 × 10-34 J s.
![]()
Question 28.
Parameters of blue and red light are 400 nm and 750 nm respectively. Which of the two is of higher energy?
Answer:
400 nm and 750 nm are the wavelengths of blue and red light respectively. Energy of radiation is given by the expression E = hν and the frequency (ν), of radiation is related to the wavelength by the expression.
ν = \(\frac{c}{\lambda}\)
∴ E = \(\frac{\mathrm{hc}}{\lambda}\)
Therefore, shorter the wavelength, λ, larger the frequency, ν, and higher the energy, E. Thus, blue light which has shorter λ (400 nm) than red light (750 nm) has higher energy.
Question 29.
What is an emission spectrum?
Answer:
- When a substance is irradiated with electromagnetic radiation, it absorbs energy. Atoms, molecules or ions, which have absorbed radiation are said to be ‘excited’. Heating can also result in an excited state.
- The excited species emits the absorbed energy in the form of radiation. This process is called emission of radiation and the recorded spectrum of this emitted radiation is called ‘emission spectrum’.
Question 30.
Give some examples of commonly used light sources that work on atomic emission.
Answer:
Examples are fluorescent tube, sodium vapor lamp, neon sign and halogen lamp.
Question 31.
Write a short note on emission spectrum of hydrogen. Also, list all the five series of lines in the hydrogen spectrum.
Answer:
i. When electric discharge is passed through gaseous hydrogen, it emits radiation. The recorded spectrum of this emitted radiation is called hydrogen emission spectrum.
ii. This spectrum falls in different regions of electromagnetic radiation and it is comprised of a series of lines corresponding to different frequencies. That is, the spectrum was discontinuous.
iii. In the year, 1885, Balmer expressed the wave numbers of the emission lines in the visible region of electromagnetic spectrum by the formula:
\(\overline{\mathrm{v}}=109677\left[\frac{1}{2^{2}}-\frac{1}{\mathrm{n}^{2}}\right] \mathrm{cm}^{-1}\)
where, n = 3, 4, 5,…
These lines are known as Balmer series.
iv. Rydberg found that other series of lines could be described by the following formula:
\(\bar{v}=109677\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right] \mathrm{cm}^{-1}\)
where, 109677 cm-1 is called Rydberg constant for hydrogen (RH).
v. Different series of emission spectral lines for hydrogen are as follows:
| Series | n1 | n2 | Region |
| Lyman | 1 | 2, 3, 4, …. | Ultraviolet |
| Balmer | 2 | 3, 4, 5, …. | Visible |
| Paschen | 3 | 4, 5, 6, …. | Infrared |
| Bracket | 4 | 5, 6, 7, …. | Infrared |
| Pfund | 5 | 6, 7, 8,…. | Infrared |
![]()
Question 32.
Observe the emission spectrum of hydrogen and answer the following questions.
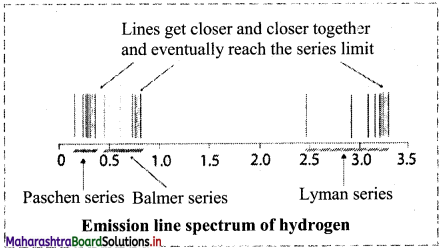
i. Is the spectrum continuous?
ii. In which region of electromagnetic radiation does the Paschen series belong?
iii. Which series falls in the visible region of electromagnetic radiation?
Answer:
i. The spectra is not continuous and comprises of a series of lines corresponding to different frequencies.
ii. Paschen series falls in the infrared region of electromagnetic radiation.
iii. Balmer series falls partly in the visible region of electromagnetic radiation.
Question 33.
Give the expression to calculate wavenumber of the emission lines in the Balmer series.
Answer:
\(\bar{v}=109677\left[\frac{1}{2^{2}}-\frac{1}{\mathrm{n}^{2}}\right] \mathrm{cm}^{-1}\)
where, n = 3, 4, 5, ….
Question 34.
Visible light has wavelengths ranging from 400 nm (violet) to 750 nm (red). Express these wavelengths in terms of frequency (Hz). (1 nm = 10-9 m)
Solution:
Given: Wavelengths: λ1 = 400 nm (for violet light), λ2 = 750 nm (for red light)
To find: Frequencies: ν1, ν2
Formula: ν = \(\frac{c}{\lambda}\)
Calculation: i. Wavelength of violet light, λ1 = 400 nm = 400 × 10-9 m
Frequency, ν = \(\frac{c}{\lambda}\) where c is speed of light = 3.0 × 108 ms-1
∴ ν1 = \(\frac{3.0 \times 10^{8} \mathrm{~ms}^{-1}}{400 \times 10^{-9} \mathrm{~m}}\) = 7.50 × 1014 Hz
ii. Wavelength of red light, λ2 = 750 nm = 750 × 10-9 m
Frequency, ν = \(\frac{c}{\lambda}\)
∴ ν2 = \(\frac{3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{750 \times 10^{-9} \mathrm{~m}}\) = 4.00 × 1014 Hz
Ans: The frequency of violet light is 7.50 × 1014 Hz and that of red light is 4.00 × 1014 Hz.
Question 35.
Yellow light emitted from a lamp has a wavelength of 580 nm. Find the frequency and wavenumber of this light.
Solution:
Given: Wavelength (λ) = 580 nm
To find: Frequency (ν), Wave number \(\bar{v}\)
Formulae : \(v=\frac{c}{\lambda}, \bar{v}=\frac{1}{\lambda}\)
Calculation: Wavelength of yellow light (λ) = 580 nm = 580 × 10-9 m [1 nm = 10-9 m]
We know that frequency (ν) is related to wavelength as: ν = \(\frac{c}{\lambda}\)
where, c, velocity of light = 3.0 × 10-8 m s-1
∴ ν = \(\frac{3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{580 \times 10^{-9} \mathrm{~m}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)
Again, Wave number, \(\bar{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-9} \mathrm{~m}}=1.72 \times 10^{6} \mathrm{~m}^{-1}\)
Ans: Frequency = 5.17 × 1014 s-1 and wave number = 1.72 × 106 m-1
Question 36.
Calculate the energy of a photon of radiation having wavelength 300 nm. [h = 6.63 × 10-34 J s]
Solution:
Given: Wavelength (λ) = 300 nm
To find: Energy of a photon (E)
Formulae: E = \(\frac{\mathrm{hc}}{\lambda}\)
Calculation: From formula,
E = \(\frac{6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}}{300 \times 10^{-9} \mathrm{~m}}=6.63 \times 10^{-19} \mathrm{~J}\)
Ans: Energy of a photon is 6.63 × 10-19 J.
![]()
Question 37.
Explain briefly the results of Bohr’s theory for hydrogen atom.
Answer:
i. The stationary states for electrons are numbered n = 1, 2, 3……. These integers are known as principal quantum numbers.
ii. The radii of the stationary states are rn = n2 a0, where a0 = 52.9 pm (picometer). Thus, the radius of the first stationary state, called the Bohr radius is 52.9 pm.
iii. The most important property associated with the electron is the energy of its stationary state. It is given by the formula:
En = -RH (1/n2), where n = 1, 2, 3, …..
RH is the Rydberg constant for hydrogen and its value in joules is 2.18 × 10-18 J.
The lowest energy state is called the ground state. Energy of the ground state (n = 1) is:
E1 = -2.18 × 10-18 × 1/12 = -2.18 × 10-18 J
Energy of the stationary state corresponding to n = 2 is
E2 = -2.18 × 10-18 × (1/(2)2) = -0.545 × 10-18 J.
iv. Bohr theory can be applied to hydrogen like species. For example, He+, Li2+, Be3+ and so on. Energies and radii of the stationary states associated with these species are given by:
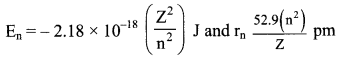
where, Z is the atomic number. From the above expressions, it can be seen that the energy decreases (becomes more negative) and radius becomes smaller as the value of Z increases.
v. Velocities of electrons can also be calculated from the Bohr theory. Qualitatively, it is found that the magnitude of velocity of an electron increases with increase of Z and decreases with increase in the principal quantum number (n).
Question 38.
How many electrons are present in \({ }_{1}^{2} \mathrm{H}\), 2He and He+ ? Which of these are hydrogen-like species?
Answer:
Hydrogen-like species contain only one electron.
Consider \({ }_{1}^{2} \mathrm{H}\):
Number of protons = Number of electrons = 1
Consider 2He:
Number of protons = Number of electrons = 2
Consider He+:
Number of electrons = (Number of electrons in He – 1) = 2 – 1 = 1
Thus, \({ }_{1}^{2} \mathrm{H}\) and He+ are hydrogen-like species.
[Note: Bohr’s theory is applicable to hydrogen atom and hydrogen-like species, which contain only one electron.]
Question 39.
Describe how the line spectrum of hydrogen is explained by Bohr theory.
Answer:
i. According to second postulate of Bohr theory, radiation is emitted when an electron moves from an outer orbit of higher principal quantum number (ni) to an inner orbit of lower principal quantum number (nf). The energy difference (ΔE) between the initial and final orbit of the electronic transition corresponds to the energy of the emitted radiation.
ii. From the third postulate of Bohr theory, ΔE can be expressed as
ΔE = Ei – Ef …….(1)
iii. According to the results derived from Bohr theory, the energy (En) of an orbit is related to its principal quantum number ‘n’ by the equation:
E = \(-\mathrm{R}_{\mathrm{H}}\left(\frac{1}{\mathrm{n}^{2}}\right)\) ……(2)
iv. On combining these two equations, we get:
![]()
v. Substituting the value of RH in joules, we get
![]()
vi. This expression can be rewritten in the terms of wavenumber of the emitted radiation in the following steps:
(ΔE) J = (h) J s × (ν) Hz
and
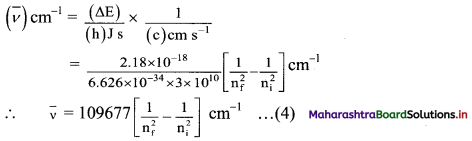
This equation appears like the Rydberg equation, where, nf = n1 and ni = n2.
In other words, Bohr theory successfully accounts for the empirical Rydberg equation for the line emission spectrum of hydrogen.
Question 40.
Observe the following diagram showing electronic transition in the hydrogen spectrum.
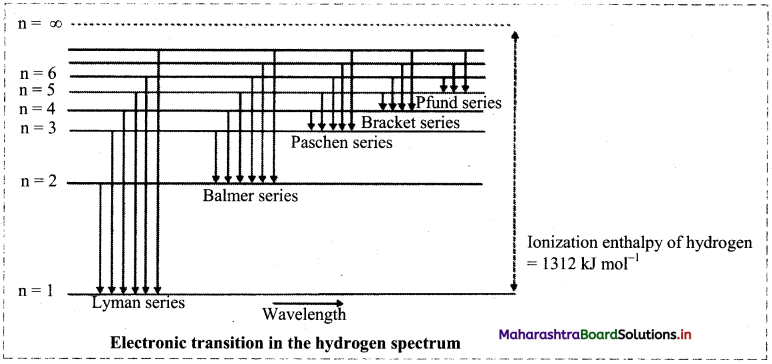
i. Electron jumps from higher energy level to n = 1. Which series does it correspond to?
ii. Electron jumps from higher energy level to n = 4. Which series does it correspond to?
iii. Which transition will give second line of Balmer series?
Answer:
i. When electron jumps from higher energy level to n = 1, it corresponds to Lyman series.
ii. When electron jumps from higher energy level to n = 1, it corresponds to Bracket series.
iii. When electron jumps from n = 4 to n = 1, the second line of Balmer series is observed.
![]()
Question 41.
Explain de Broglie’s equation.
Answer:
de Broglie’s equation:
- de Broglie proposed (in 1924) that matter should exhibit a dual behaviour. That is, every object which possesses a mass and velocity behaves both as a particle and as a wave. An electron has mass and velocity. This means that an electron should have momentum (p), a property of particle as well as wavelength (λ), a property of wave.
- According to de Broglie, the wavelength λ of a particle of mass m moving with a velocity v is
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) where, h is Planck’s constant. - The quantity mv gives the momentum of the particles.
λ = \(\frac{\mathrm{h}}{\mathrm{p}}\) where, p represents the momentum of the particle. - de Broglie’s prediction was confirmed by diffraction experiments (a wave property).
[Note: According to de Broglie’s equation, the wavelength of a moving particle is inversely proportional to its mass. Therefore, heavier particles have much smaller wavelength than lighter particles like electrons.]
Question 42.
Write a note on Heisenberg’s uncertainty principle.
Answer:
i. Uncertainty principle was proposed by Wemer Heisenberg in 1927. It can be stated as “It is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron ”.
ii. If Δx is the uncertainty in the determination of the position of a very small moving particle and Δpx is the uncertainty in the determination of its momentum, then
Δx Δpx ≥ \(\frac{\mathrm{h}}{4 \pi}\) …….(1) where h is Planck’s constant
iii. The above equation can alternatively be stated as,
Δx × m × Δvx ≥ \(\frac{\mathrm{h}}{4 \pi}\), because Δpx = m × Δvx ……..(2)
where Δvx is the uncertainty in the determination of velocity and m is the mass of the particle.
Question 43.
Calculate the radius and energy associated with the first orbit of He.
Solution:
Given: n = 1
To find: Radius and energy associated with the first orbit of He+
Formulae:
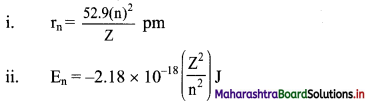
Calculation: He+ is a hydrogen-like species having Z = 2.
Using formula (i),
Radius of the first orbit of He+ = r1 = \(\frac{52.9 \times(1)^{2}}{2} \mathrm{pm}\)
= 26.45 pm
Using formula (ii),
Energy of the first orbit of He+ = E1 = -2.18 × 10-18 \(\left(\frac{2^{2}}{1^{2}}\right) \mathrm{J}\)
= -8.72 × 10-18 J
Ans: Radius of the first orbit of He+ is 26.45 pm and energy of the first orbit of He+ is -8.72 × 10-18 J.
Question 44.
What is the wavelength of the photon emitted during the transition from the orbit of n = 5 to that of n = 2 in hydrogen atom?
Solution:
Given: ni = 5, nf = 2
To find: Wavelength of the photon emitted

Ans: Wavelength of the photon emitted is 434 nm.
Question 45.
Calculate the mass of a hypothetical particle having wavelength 5894 A and velocity 1.0 × 108 ms-1.
Solution:
Given: Wavelength (λ) = 5894 Å, Velocity (ν) = 1.0 × 108 ms-1
To find: Mass of a particle
Formula: λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) or m = \(\frac{\mathrm{h}}{\lambda \mathrm{v}}\) (according to de-Broglie equation)
Calculation: m = \(\frac{\mathrm{h}}{\lambda \mathrm{v}}\)
∴ m = \(\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}}{\left(5894 \times 10^{-10} \mathrm{~m}\right) \times\left(1.0 \times 10^{8} \mathrm{~ms}^{-1}\right)}\)
= 1.124 × 10-35 kg
Ans: Mass of a particle is 1.124 × 10-35 kg.
[Calculation using log table:
\(\frac{6.626 \times 10^{-34}}{5894 \times 10^{-10} \times 1.0 \times 10^{8}}=\frac{6.626}{5894} \times 10^{-32}\)
= Antilog10 [log10 6.626 – log10 5894] × 10-32
= Antilog10 [0.8213 – 3.7704] × 10-32
= Antilog10 [latex]\overline{3} .0509[/latex] × 10-32 = 1.124 × 10-35]
![]()
Question 46.
Write a short note on Schrodinger equation.
Answer:
Schrodinger equation or wave equation:
i. Schrodinger developed the fundamental equation of quantum mechanics which incorporates wave particle duality of matter. The Schrodinger equation or wave equation is written as:
It \(\hat{\mathbf{H}}\)ψ = Eψ
Here \(\hat{\mathbf{H}}\) is a mathematical operator called Hamiltonian, ψ (psi) is the wave function and E is the total energy of the system.
ii. When Schrodinger equation is solved for an electron in hydrogen atom, the possible values of energy states (E) that the electron may have along with the corresponding wave function (ψ) are obtained. As a consequence of solving this equation, a set of three quantum numbers characteristic of the quantized energy levels and the corresponding wave functions are obtained. These are: Principal quantum number (n), azimuthal quantum number (l) and magnetic quantum number (ml).
iii. The solution of Schrodinger wave equation led to three quantum numbers and successfully predicted features of hydrogen atom emission spectrum.
iv. Splitting of spectral lines in multi-electron atomic emission spectra could not be explained through such model. These were explained by George Uhlenbeck and Samuel Goudsmit (1925) who proposed the presence of the fourth quantum number called electron spin quantum number, ms.
Question 47.
Write a short note on magnetic orbital quantum number (ml).
Answer:
Magnetic orbital quantum number (ml):
- Magnetic orbital quantum number describes the relative spatial orientation of the orbitals in a given subshell.
- It is denoted by m; and it has values from -l to +l through zero, giving total values or total orientations equal to (2l + 1).
- For s-subshell, 1 = 0, hence, ml = 0. Thus, s-subshell contains only one orbital.
- For p-subshell, l = 1, hence, ml = +1, 0, -1. Thus, p-subshell contains three orbitals having distinct orientations.
Question 48.
If n = 2, what are the values of quantum number l and ml ?
Answer:
For a given n, l = 0 to (n – 1) and for given l, ml = -l…., 0…. + l
Therefore, the possible values of l and ml for n = 2 are:
| Value of n | Value of l | Value of ml |
| 2 | 0 | ml = 0 |
| 1 | ml = -1
ml = 0 ml = +1 |
Question 49.
What are the values of ml for f-subshell?
Answer:
For f-subshell, l = 3. Therefore, ml has seven values: + 3, + 2, + 1, 0, -1, -2, -3.
![]()
Question 50.
How many orbitals make the N-shell? What is the subshell wise distribution of orbitals in the N-shell?
Answer:
For N-shell principal quantum number n = 4
∴ Total number of orbitals in N-shell = n2 = 42 = 16. The total number of subshells in N-shell = n = 4.
The four subshells with their azimuthal quantum numbers and the constituent number of orbitals are as shown below:
| Azimuthal quantum number (l) | Symbol of subshell | Number of orbitals (2l + 1) |
| l = 0 | s | (2 × 0) + 1 = 1 |
| l = 1 | P | (2 × 1) + 1 = 3 |
| l = 2 | d | (2 × 2) + 1 = 5 |
| l = 3 | f | (2 × 3) + 1 = 7 |
Question 51.
Complete the following flow chart:
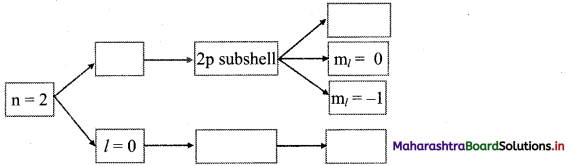
Answer:
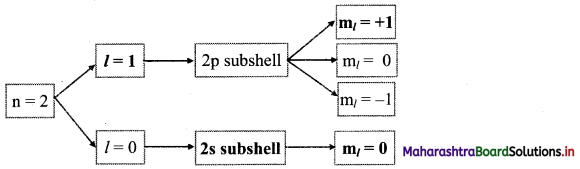
Question 52.
Write a short note on electron spin quantum number.
Answer:
Electron spin quantum number (ms):
- Electron spin quantum number describes the spin state of the electron in an orbital. It is designated as ms.
- An electron spins around its axis and this imparts spin angular momentum to it.
- The two orientations which the spin angular momentum of an electron can take up give rise to the spin states which can be distinguished from each other by the spin quantum number, ms, which can be either +1/2 or -1/2.
- The two spin states are represented by two arrows, ↑ (pointing up) and ↓ (pointing down) and thus have opposite spins.
Question 53.
An atom has two electrons in its 4s orbital. Write the values of the four quantum numbers for each of them.
Answer:
For the 4s orbital, 4 stands for the principal quantum number n; s stands for the subshell s having the value of azimuthal quantum number, l = 0. In the ‘s’ subshell, there is only one orbital and has magnetic quantum number, ml = 0. The two electrons in this orbital have opposite spins. Thus, the four quantum numbers of two electrons in 4s orbital are:

![]()
Question 54.
Write a short note on probability density of electron.
Answer:
i. The probability of finding an electron at a given point in an atom is proportional to the square of the wave function at that point (ψ2).
ii. According to Max Born, the square of wave function at a point in an atom is the probability density of the electron at that point.
The following figure shows the probability density diagrams of Is and 2s atomic orbitals. These diagrams appear like a cloud.
The electron cloud of 2s orbital shows one node, which is a region with nearly zero probability density and displays the change of sign for its corresponding wavefunction.
Diagram:
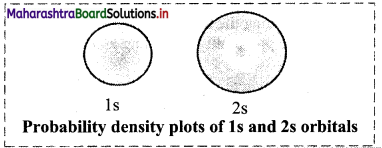
Question 55.
What is meant by the term ‘boundary surface diagram’?
Answer:
A boundary surface is drawn in space for an orbital such that the value of probability density (ψ2) is constant and encloses a region where the probability of finding electron is typically more than 90%. Such a boundary surface diagram is a good representation of shape of an orbital.
e.g. Boundary surface diagram of Is and 2s orbitals are spherical in shape.
Question 56.
Describe the shape of s orbital.
Answer:
Shape of s orbital:
- For each value of principal quantum number ‘n’, there is only one s-orbital.
- For s-orbital, l = 0 and ml = 0, hence s-orbital has only one orientation i.e., the probability of finding the electrons is same in all directions. Thus, s-orbital is spherically symmetrical around the nucleus.
- The value of n determines the size of an orbital. With increase in the value of n, the size of the s-orbital increases.
Diagram:
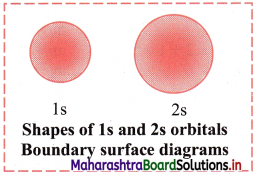
Question 57.
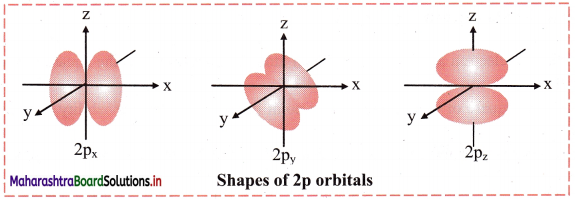
Describe the shape of 2p orbitals.
Answer:
Shape of 2p orbitals:
i. For p orbital, l = 1. For l = 1, ml = +1, 0, -1. Thus, p orbitals have three orientations.
ii. Each orbital has two lobes on the two sides of a nodal plane passing through the nucleus.
iii. Shape of 2p orbitals resembles a dumbbell.
iv. The size and energy of the three 2p orbitals are the same. However, their orientations in space are different. The lobes of the three 2p orbitals are along the x, y and z axes. Accordingly, the corresponding orbitals are designated as 2px, 2py and 2pz. The size and energy of the orbitals in p subshell increase with the increase of principal quantum number.
Diagram:
Question 58.
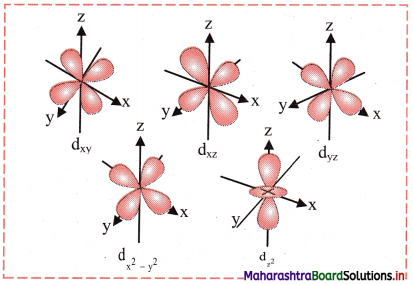
Describe the shape of 3d orbitals.
Answer:
Shape of 3d orbitals:
- For d orbital, l = 2. For l = 2, ml = +2, +1, 0, -1, -2. Thus, d orbitals have five orientations.
- They are designated as dxy, dyz, dzx, dx2-y2 and dz.
- Shape of 3d orbitals are shown in the following figure. The first three have double dumb-bell shape. They lie in xy, yz and xz plane, respectively. The dx2-y2 is also dumb-bell shaped and lies along the x and y axes. dz2 is dumb-bell shaped along z axis with a dough-nut shaped ring of high electron density around the nucleus in xy plane.
- In spite of difference in their shapes, the five d orbitals are equivalent in energy. The shapes of 4d, 5d, 6d…….. orbitals are similar to those of 3d orbitals, but their respective size and energies are large or they are said to be more diffused.
Diagram:
![]()
Question 59.
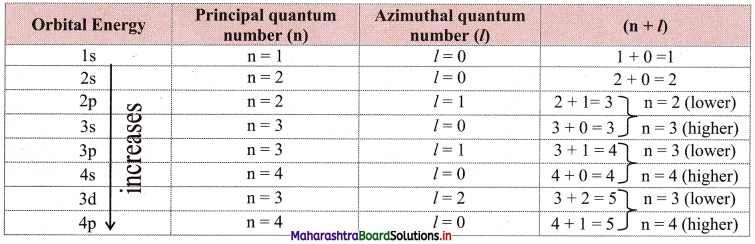
Explain (n + l) rule with respect to energies of orbitals.
Answer:
The lower the sum (n + l) for an orbital, the lower is its energy. If two orbitals have the same (n + l) values, then the orbital with the lower value of n is of lower energy. This is called the (n + l) rule.
Question 60.
What are the two methods of representing electronic configuration of an atom?
Answer:
The two methods of representing electronic configuration of an atom are:
i. Orbital notation: nsa npb ndc …..
In the orbital notation method, a shell is represented by the principal quantum number (n) followed by respective symbol of the subshell. The number of electrons occupying that subshell being written as superscript on right side of the symbol.
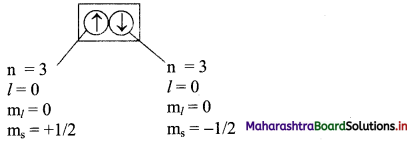
ii. Orbital diagram:
In the orbital diagram method, each orbital in a subshell is represented by a box and the electrons represented by an arrow (↑ for up spin and ↓ for down spin) are placed in the respective boxes. In this method, all the four quantum numbers of electron are accounted for.

Note: Consider two electrons in 3s orbital:
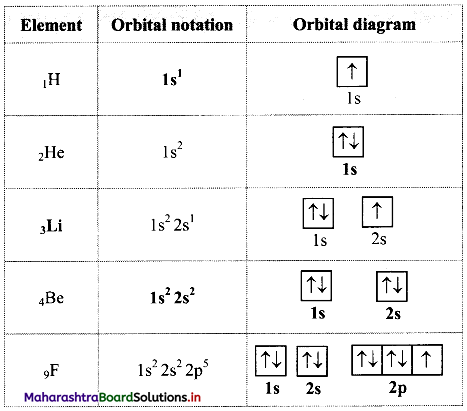
Question 61.
Complete the following table:
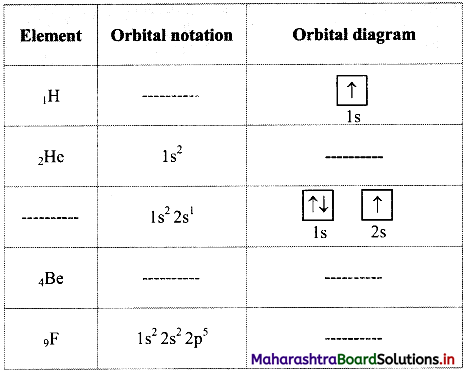
Answer:
Question 62.
Explain condensed orbital notation of electronic configuration of an atom.
Answer:
- The orbital notation of electronic configuration of an element with high atomic number comprises a long train of symbols of orbitals with an increasing order of energy.
- It can be condensed by dividing it into two parts: Inner or core part of electronic configuration and outer electronic configuration.
- Electronic configuration of the preceding inert gas is a part of the electronic configuration of any element. In the condensed orbital notation, it is implied by writing symbol of that inert gas in a square bracket. It is core part of the electronic configuration of that element. The outer electronic configuration is specific to a particular element and written immediately after the bracket.
- For example, the orbital notation of potassium ‘K (Z = 19) is Is2 2s2 2p6 3s2 3p6 4s1’. Its core part is the electronic configuration of the preceding inert gas argon ‘Ar: 1s2 2s2 2p6 3s2 3p6, while ‘4s1’ is an outer part. Therefore, the condensed orbital notation of electronic configuration of potassium is ‘K: [Ar] 4s2.’
Note: Electronic configuration of the elements with atomic numbers 1 to 30 is as follows:
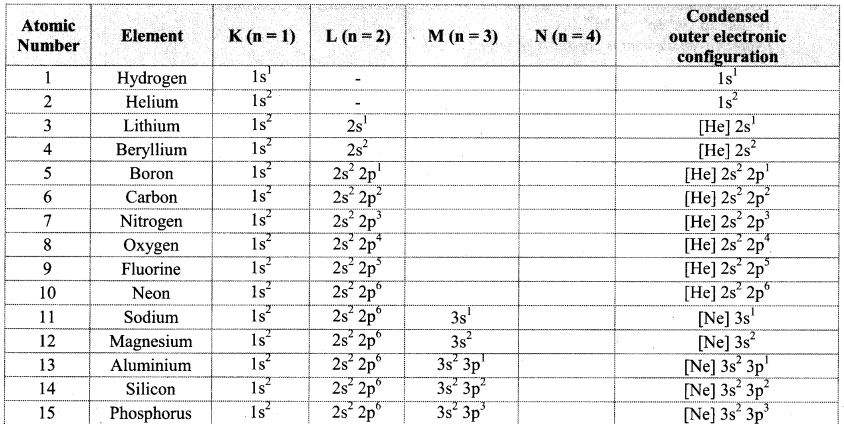
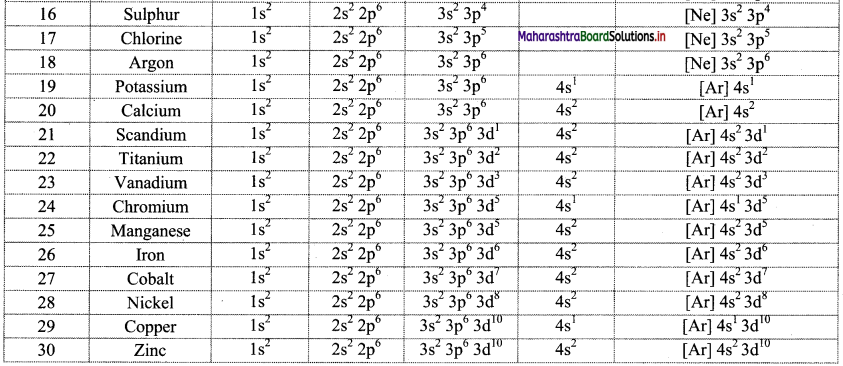
![]()
Question 63.
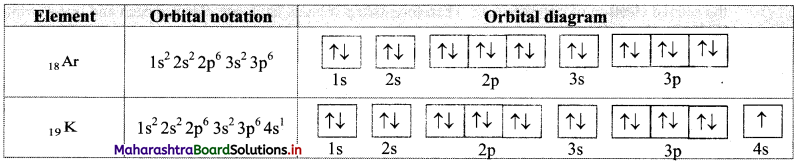
Write electronic configuration of 18Ar and 19K using orbital notation and orbital diagram method.
Answer:
From the atomic numbers, it is understood that 18 electrons are to be filled in Ar atom and 19 electrons are to be filled in K atom. These are to be filled in the orbitals according to the Aufbau principle. The electronic configuration of these atoms can be represented as:
Question 64.
Write condensed orbital notation of electronic configuration of the following elements:
i. Fluorine (Z = 9)
ii. Scandium (Z = 21)
iii. Cobalt (Z = 27)
iv. Zinc (Z = 30)
Answer:
| No. | Element | Condensed orbital notation |
| i. | Fluorine (Z = 9) | [He] 2s2 2p5 |
| ii. | Scandium (Z = 21) | [Ar] 4s2 3d1 |
| iii. | Cobalt (Z = 27) | [Ar] 4s2 3d7 |
| iv. | Zinc (Z = 30) | [Ar] 4s2 3d10 |
Question 65.
Find out one dinegative anion and one unipositive cation which are isoelectronic with Ne atom. Write their electronic configuration using orbital notations and orbital diagram method.
Answer:
Atomic number (Z) of Ne is 10. Therefore, Ne and its isoelectronic species contain 10 electrons each. The dinegative anionic species, isoelectronic with Ne is obtained by adding two electrons to the atom with Z = 8. This is O2- ion.
The unipositive cationic species, isoelectronic with Ne is obtained by removing one electron from an atom with Z = 11. It is Na+ ion.
These species and their electronic configurations are shown below:

Question 66.
A student pictorially represented the electronic configuration of cobalt (Z = 27) in ground state as shown in the following figure.

i. Is this the correct representation?
ii. Identify the rules of electron filling that are violated (if any) in the above answer and give the correct representation.
Answer:
i. No, the electronic configuration of cobalt in ground state is incorrectly represented.
ii. The mles of electron filling that are violated in the above diagram are Pauli’s exclusion principle and Hund’s rule. The correct electronic configuration is:

Question 67.
With reference to the representative model of the gold foil experiment, answer the following questions:
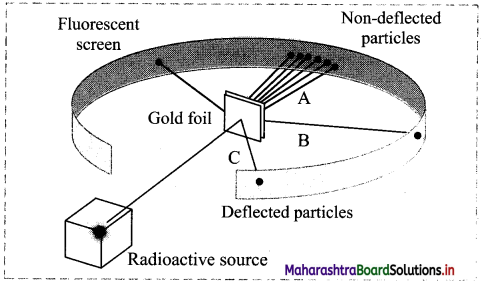
i. What evidence regarding an atom do lines A, B and C provide?
ii. How does Rutherford’s model contradict Thomson’s plum-pudding model?
iii. What results would you expect from the experiment if Thomson’s plum-pudding model was correct?
Answer:
i. Line A – Most of the space inside the atom is empty because most of the α-particles passed through the gold foil without getting deflected.
Line B – The nucleus is positively charged since some α-particles were deflected at small angles.
Line C – The nucleus contains most of the atoms mass since few α-particles were deflected backward, i.e. toward the radioactive source.
ii. According to plum-pudding model, an atom was considered a positively charged sphere with negatively charged electrons embedded in it. However, Rutherford’s gold foil experiment proved that an atom consists of large empty space with positive charge concentrated only at the centre (nucleus) and negatively charged electrons revolve around the nucleus in various orbits.
iii. If Thomson’s plum-pudding model was correct, then in the gold foil experiment we would not expect to see any significant deflection of the α-particles, i.e., Most α-particles would pass through the foil with very small or no deflections.
![]()
Question 68.
Complete the following table:

Answer:

Multiple Choice Questions
1. Which of the following statements about the electron is INCORRECT?
(A) It is a negatively charged particle.
(B) The mass of electron is equal to the mass of neutron.
(C) It is a basic constituent of all atoms.
(D) It is a constituent of cathode rays.
Answer:
(B) The mass of electron is equal to the mass of neutron.
2. The isotopes of an element differ in
(A) the number of neutrons in the nucleus
(B) the charge on the nucleus
(C) the number of extra-nuclear electrons
(D) both the nuclear charge and the number of extra-nuclear electrons
Answer:
(A) the number of neutrons in the nucleus
3. The difference between U235 and U238 atoms is that U238 contains ………….
(A) 3 more protons
(B) 3 more protons and 3 more electrons
(C) 3 more neutrons and 3 more electrons
(D) 3 more neutrons
Answer:
(D) 3 more neutrons
![]()
4. The number of electrons, protons and neutrons in 31P3- ion is respectively ……………
(A) 15, 15, 16
(B) 15, 16, 15
(C) 18, 15, 16
(D) 15, 16, 18
Answer:
(C) 18, 15, 16
5. In vacuum, the speed of all types of electromagnetic radiation is equal to ………….
(A) 3.0 × 106 m s-1
(B) 3.0 × 108 m s-1
(C) 3.0 × 1010 m s-1
(D) 3.0 × 1012 m s-1
Answer:
(B) 3.0 × 108 m s-1
6. In the electromagnetic spectrum, the ultraviolet region is around ………….. Hz.
(A) 106
(B) 1010
(C) 1016
(D) 1026
Answer:
(C) 1016
7. In hydrogen spectrum, the series of lines appearing in ultraviolet region of electromagnetic spectrum are called ………….
(A) Lyman series
(B) Balmer series
(C) Pfund series
(D) Brackett series
Answer:
(A) Lyman series
8. The energy of electron in the nth Bohr orbit of H-atom is …………
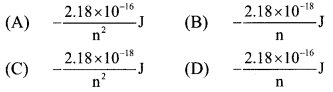
Answer:
(C) \(-\frac{2.18 \times 10^{-18}}{\mathrm{n}^{2}} \mathrm{~J}\)
9. Which of the following is a hydrogen-like species?
(A) He2+
(B) Be3+
(C) Li+
(D) H+
Answer:
(B) Be3+
![]()
10. The de Broglie wavelength associated with a particle of mass 10-6 kg moving with a velocity of 10 m s-1 is ………..
(A) 6.63 × 10-22 m
(B) 6.63 × 10-29 m
(C) 6.63 × 10-31 m
(D) 6.63 × 10-34 m
Answer:
(B) 6.63 × 10-29 m
11. An orbital is designated by …………. quantum numbers while an electron in an atom is designated by …………. quantum numbers.
(A) two, three
(B) three, two
(C) four, two
(D) three, four
Answer:
(D) three, four
12. In a multi-electron atom, the energy of the orbital depends on two quantum numbers: ……….
(A) n and ms
(B) n and ml
(C) ml and ms
(D) n and l
Answer:
(D) n and l
13. The number of subshells in a shell is equal to ………..
(A) n
(B) n2
(C) n – 1
(D) l + 1
Answer:
(A) n
14. The maximum number of electrons in a subshell for which l = 3 is …………..
(A) 14
(B) 10
(C) 8
(D) 4
Answer:
(A) 14
![]()
15. Which of the following is INCORRECT?
(A) A nodal plane has ψ2 very close to zero.
(B) The value of ψ2 at any finite distance from the nucleus is always zero.
(C) A boundary surface diagram enclosing 100 % probability density cannot be drawn.
(D) A boundary surface diagram is a good representation of shape of an orbtial.
Answer:
(B) The value of ψ2 at any finite distance from the nucleus is always zero.
16. pz-Orbital has ……….. nodal plane/planes.
(A) zero
(B) one
(C) two
(D) three
Answer:
(B) one
17. Which of the following pairs of d-orbitals will have electron density along the axis?
(A) dxy, dx2-y2
(B) dz2, dxz
(C) dxz, dyz
(D) dz2, dx2-y2
Answer:
(D) dz2, dx2-y2
18. The two electrons have the following set of quantum numbers:
P = 3, 2, -2, +\(\frac {1}{2}\)
Q = 3, 0, 0, +\(\frac {1}{2}\)
Which of the following statement is TRUE?
(A) P and Q have same energy
(B) P has greater energy than Q
(C) P has lesser energy than Q
(D) P and Q represent same electron
Answer:
(B) P has greater energy than Q
19. For 3d orbital, the values of n and l are ………… respectively.
(A) 0, 3
(B) 3, 2
(C) 3, 0
(D) 3, 3
Answer:
(B) 3, 2
20. For the electron present in 1 s orbital of helium atom, the correct set of values of quantum numbers is ………..
(A) 1, 0, 0, +1/2
(B) 1, 1, 0, +1/2
(C) 1, 1, 1, +1/2
(D) 2, 0, 0, +1/2
Answer:
(A) 1, 0, 0, +1/2
![]()
21. The ground state electronic configuration for chromium atom (Z = 24) is …………
(A) [Ar] 3d5 4s1
(B) [Ar] 3d4 4s2
(C) [Ar] 3d8
(D) [Ar] 4s1 4p5
Answer:
(A) [Ar] 3d5 4s1
22. The electronic configuration of Ni2+ is ……….. (Atomic number of Ni = 28)
(A) [Ar] 4s2 3d6
(B) [Ar] 4s1 3d8
(C) [Ar] 3d8
(D) [Ar] 4s2 3d8
Answer:
(C) [Ar] 3d8