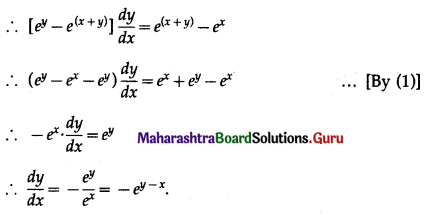Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Ex 3.4 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Differentiation Ex 3.4
1. Find \(\frac{d y}{d x}\) if:
Question 1.
√x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get

Question 2.
x3 + y3 + 4x3y = 0
Solution:
x3 + y3 + 4x3y = 0
Differentiating both sides w.r.t. x, we get

![]()
Question 3.
x3 + x2y + xy2 + y3 = 81
Solution:
x3 + x2y + xy2 + y3 = 81
Differentiating both sides w.r.t. x, we get

2. Find \(\frac{d y}{d x}\) if:
Question 1.
y.ex + x.ey = 1
Solution:
y.ex + x.ey = 1
Differentiating both sides w.r.t. x, we get

Question 2.
xy = e(x-y)
Solution:
xy = e(x-y)
∴ log xy = log e(x-y)
∴ y log x = (x – y) log e
∴ y log x = x – y …..[∵ log e = 1]
∴ y + y log x = x
∴ y(1 + log x) = x
∴ y = \(\frac{x}{1+\log x}\)

![]()
Question 3.
xy = log(xy)
Solution:
xy = log (xy)
∴ xy = log x + log y
Differentiating both sides w.r.t. x, we get

3. Solve the following:
Question 1.
If x5 . y7 = (x + y)12, then show that \(\frac{d y}{d x}=\frac{y}{x}\)
Solution:
x5 . y7 = (x + y)12
∴ log(x5 . y7) = log(x + y)12
∴ log x5 + log y7 = log(x + y)12
∴ 5 log x + 7 log y = 12 log (x + y)
Differentiating both sides w.r.t. x, we get


Question 2.
If log(x + y) = log(xy) + a, then show that \(\frac{d y}{d x}=\frac{-y^{2}}{x^{2}}\)
Solution:
log (x + y) = log (xy) + a
∴ log(x + y) = log x + log y + a
Differentiating both sides w.r.t. x, we get

![]()
Question 3.
If ex + ey = e(x+y), then show that \(\frac{d y}{d x}=-e^{y-x}\).
Solution:
ex + ey = e(x+y) ……….(1)
Differentiating both sides w.r.t. x, we get