Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.6 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.6
Question 1.
Find the sum \(\sum_{r=1}^{n}(r+1)(2 r-1)\).
Solution:

Question 2.
Find \(\sum_{r=1}^{n}\left(3 r^{2}-2 r+1\right)\)
Solution:
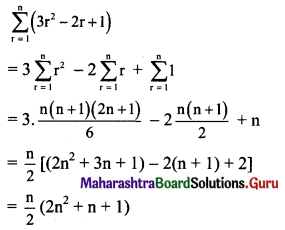
![]()
Question 3.
Find \(\sum_{r=1}^{n}\left(\frac{1+2+3 \ldots .+r}{r}\right)\)
Solution:

= \(\frac{n}{4}\) [(n + 1) + 2]
= \(\frac{n}{4}\) (n + 3)
Question 4.
Find \(\sum_{r=1}^{n}\left(\frac{1^{3}+2^{3}+\ldots . .+r^{3}}{r(r+1)}\right)\)
Solution:

Question 5.
Find the sum 5 × 7 + 9 × 11 + 13 × 15 + ….. upto n terms.
Solution:
5 × 7 + 9 × 11 + 13 × 15 + ….. upto n terms
Now, 5, 9, 13, … are in A.P. with
rth term = 5 + (r – 1) (4) = 4r + 1
7, 11, 15, ….. are in A.P. with
rth term = 7 + (r – 1) (4) = 4r + 3
∴ 5 × 7 + 9 × 11 + 13 × 15 + …… upto n terms

![]()
Question 6.
Find the sum 22 + 42 + 62 + 82 + ….. upto n terms.
Solution:

Question 7.
Find (702 – 692) + (682 – 672) + (662 – 652) + …… + (22 – 12)
Solution:
Let S = (702 – 692) + (682 – 672) + …… + (22 – 12)
∴ S = (22 – 12) + (42 – 32) + ….. + (702 – 692)
Here, 2, 4, 6,…, 70 are in A.P. with rth term = 2r
and 1, 3, 5, …,69 are in A.P. with rth term = 2r – 1

Question 8.
Find the sum 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… + (2n – 1) (2n + 1) (2n + 3)
Solution:
Let S = 1 × 3 × 5 + 3 × 5 × 7 + ….. upto n terms
Here, 1, 3, 5, 7 … are in A.P. with rth term = 2r – 1,
3, 5, 7, 9,… are in A.P. with rth term = 2r + 1,
5, 7, 9, 11,… are in A.P. with rth term = 2r + 3
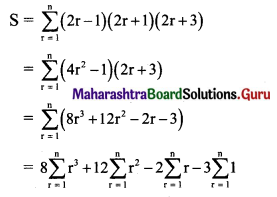

![]()
Question 9.
If \(\frac{1 \times 2+2 \times 3+3 \times 4+4 \times 5+\ldots \text { upto } n \text { terms }}{1+2+3+4+\ldots \text { upto } n \text { terms }}\) = \(\frac{100}{3}\), find n.
Solution:

Question 10.
If S1, S2 and S3 are the sums of first n natural numbers, their squares and their cubes respectively, then show that 9\(\mathrm{S}_{2}{ }^{2}\) = S3(1 + 8S1).
Solution:

