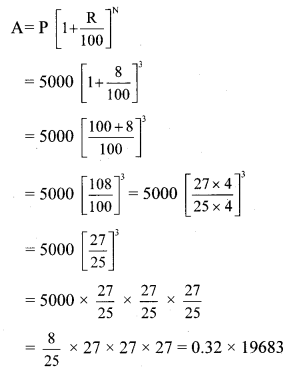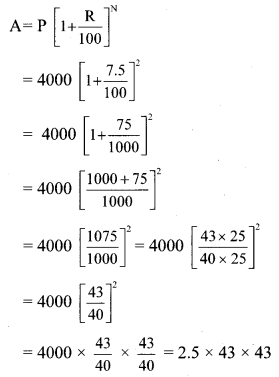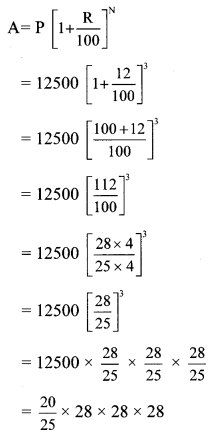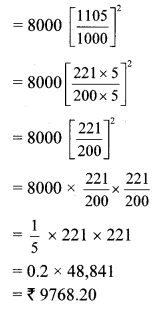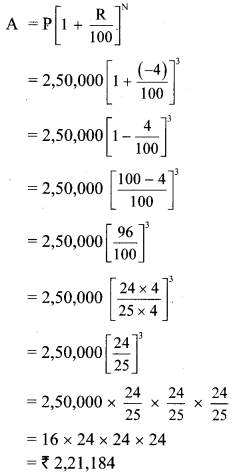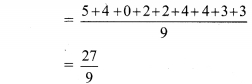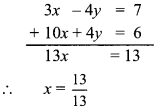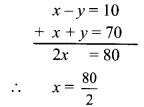Uncategorized

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.3 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.3 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
Write the following rational numbers in decimal form.
i. \(\frac { 9 }{ 37 }\)
ii. \(\frac { 18 }{ 42 }\)
iii. \(\frac { 9 }{ 14 }\)
iv. \(-\frac { 103 }{ 5 }\)
v. \(-\frac { 11 }{ 13 }\)
Solution:
i. \(\frac { 9 }{ 37 }\)

ii. \(\frac { 18 }{ 42 }\)

iii. \(\frac { 9 }{ 14 }\)

iv. \(-\frac { 103 }{ 5 }\)

v. \(-\frac { 11 }{ 13 }\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.1 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.1 8th Std Maths Answers Chapter 15 Area

Question 1.
If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
Solution:
Given, base = 18 cm, height = 11 cm
Area of a parallelogram = base × height
= 18 × 11
= 198 sq.cm
∴ Area of the parallelogram is 198 sq.cm.

Question 2.
If area of a parallelogram is 29.6 sq. cm and its base is 8 cm, find its height.
Solution:
Given, area of a parallelogram = 29.6 sq.cm,
base = 8 cm
Area of a parallelogram = base × height
∴ 29.6 = 8 × height
∴ height = \(\frac { 29.6 }{ 8 }\) = 3.7 cm
∴ Height of the parallelogram is 3.7 cm.

Question 3.
Area of a parallelogram is 83.2 sq.cm. If its height is 6.4 cm, find the length of its base.
Solution:
Given, area of a parallelogram = 83.2 sq.cm, height = 6.4 cm
Area of a parallelogram = base × height
∴ 83.2 = base × 6.4
∴ base = \(\frac { 83.2 }{ 6.4 }\) = 13 cm
∴ The length of the base of the parallelogram is 13 cm.

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.1 Intext Questions and Activities

Question 1.
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = base × height (Textbook pg. no.94)

Solution:
Draw a big enough parallelogram ABCD on a paper as shown in the figure.
Draw perpendicular AE on side BC.
Cut the right angled ∆AEB. Join it with the remaining part of ₹ABCD as shown in the figure.
The new figure formed is a rectangle.
The rectangle is formed from the parallelogram.
So, areas of both the figures are equal.
Base of parallelogram is one side (length) of the rectangle and its height is the other side (breadth) of the rectangle.
∴ Area of a parallelogram = Area of a rectangle = length × breadth = base × height

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 14.1 8th Std Maths Answers Solutions Chapter 14 Compound Interest.

Practice Set 14.1 8th Std Maths Answers Chapter 14 Compound Interest

Practice Set 14.1 Class 8 Question 1.
Find the amount and the compound interest.

No	Principal (Rs)	Rate (p.c.p.a.)	Duration (years)
i.	2000	5	2
ii.	5000	8	3
iii.	4000	7.5	2

Solution:
i. Here P = Rs 2000, R = 5 p.c.p.a. and N = 2 years

= 5 × 441
∴ A = Rs 2205
I = Amount (A) – Principal (P)
= 2205 – 2000
= Rs 205
∴ The amount is Rs 2205 and the compound interest is Rs 205.

ii. Here, P = Rs 5000, R = 8 p.c.p.a. and N = 3 years

∴ A = Rs 6298.56
I = Amount (A) – Principal (P)
= 6298.56 – 5000
= Rs 1298.56
∴ The amount is Rs 6298.56 and the compound interest is Rs 1298.56.

iii. Here, P = Rs 4000, R = 7.5 p.c.p.a. and N = 2 years

∴A = Rs 4622.50
I = Amount (A) – Principal (P)
= 4622.50 – 4000
= Rs 622.50
∴The amount is Rs 4622.50 and the compound interest is Rs 622.50.

Compound Interest Practice Set 14.1 Question 2.
Sameerrao has taken a loan of Rs 12500 at the rate of 12 p.c.p.a. for 3 years. If the interest is compounded annually then how many rupees should he pay to clear his loan?
Solution:
Here, P = Rs 12,500, R = 12 p.c.p.a. and
N = 3 years

= 0.8 × 28 × 28 × 28
= Rs 17,561.60
Sameerrao should pay Rs 17,561.60 to clear his loan.

8th Standard Maths Practice Set 14.1 Question 3.
To start a business Shalaka has taken a loan of Rs 8000 at a rate of \(10\frac { 1 }{ 2 }\) p.c.p.a. After two years how much compound interest will she have to pay?
Solution:
Here, P = Rs 8000, N = 2 years and


I = Amount (A) – Principal (P)
= 9768.20 – 8000
= Rs 1768.20
∴ After two years Shalaka will have to pay Rs 1768.20 as compound interest.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 12.2 8th Std Maths Answers Solutions Chapter 12 Equations in One Variable.

Practice Set 12.2 8th Std Maths Answers Chapter 12 Equations in One Variable

Equation In One Variable Practice Set 12.2 Question 1.
Mother is 25 years older than her son. Find son’s age, if after 8 years ratio of son’s age to mother’s age will be \(\frac { 4 }{ 9 }\).
Solution:
Let the son’s present age be x years.
∴ Mother’s present age = (x + 25) years
After 8 years,
Son’s age = (x + 8) years
Mother’s age = (x + 25 + 8) = (x + 33) years
Since, the ratio of the son’s age to mother’s age after 8 years is \(\frac { 4 }{ 9 }\).
∴ \(\frac{x+8}{x+33}=\frac{4}{9}\)
∴ 9 (x + 8) = 4 (x + 33)
∴ 9x + 72 = 4x + 132
∴ 9x – 4x = 132 – 72
∴ 5x = 60
∴ x = \(\frac { 60 }{ 5 }\)
∴ x = 12
∴ Son’s present age is 12 years.

8th Std Maths Practice Set 12.2 Question 2.
The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent to \(\frac { 1 }{ 2 }\) . Find the fraction.
Solution:
Let the numerator of the fraction be x.
The denominator of a fraction is greater than its numerator by 12.
∴ Denominator of the fraction = (x + 12)
∴ The required fraction = \(\frac { x }{ x+12 }\)
For the new fraction,
numerator is decreased by 2.
∴ The new numerator = (x – 2)
Also, denominator is increased by 7.
∴ The new denominator = (x + 12) + 7
= (x + 19)
Since, the new fraction is equivalent to \(\frac { 1 }{ 2 }\).
∴ \(\frac{x-2}{x+19}=\frac{1}{2}\)
∴ 2(x – 2) = 1(x + 19)
∴ 2x – 4 = x + 19
∴ 2x – x = 19 + 4
∴ x = 23
∴ The required fraction = \(\frac{x}{x+12}=\frac{23}{23+12}=\frac{23}{35}\)
∴ The required fraction is \(\frac { 23 }{ 35 }\)

Practice Set 12.2 Class 8 Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.

∴ Weight of copper in the brass utensil = \(\left(\frac{13}{7} x\right)\) gm
The weight of the brass utensil = 700 gm
∴ \(\frac { 13 }{ 7 }x+x=700\)
∴ \(\frac { 13 }{ 7 }x\) x × 7 + x × 7 = 700 × 7
∴ 13x + 7x = 4900
∴ 20x = 4900
∴ \(x=\frac { 4900 }{ 20 }\)
∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Practice Set 12.2 8th Class Question 4.
Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let the three consecutive whole numbers be (x – 1), x and (x + 1).
∴ Sum of the three numbers
= (x – 1) + x + (x + 1)
= 3x
Given that, the sum of the three numbers is greater than 45 and less than 54.
When the sum of the three numbers is 45,
3x = 45
∴ x = \(\frac { 45 }{ 3 }\)
∴ x = 15
When the sum of the three numbers is 54,
∴ 3x = 54
∴ x = \(\frac { 54 }{ 3 }\)
∴ x = 18
∴ the value of x is greater than 15 and less than 18.
∴ the value of x is either 16 or 17

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17

Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.

Practice Set 12.2 8th Standard Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x

	Digit in units place	Digit in tens place	Number
Original Number	x	2x	(2x × 10) + x = 20x + x = 21x
New Number	2x	x	(x × 10) + 2x = 10x + 2x = 12x

Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = \(\frac { 66 }{ 33 }\)
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.

8th Standard Maths Practice Set 12.2 Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ \(x=\frac { 33000 }{ 300 }\)
∴ x = 110
∴ 110 tickets of Rs 100 were sold.

8th Maths Practice Set 12.2 Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.

Raju Sold A Bicycle to Amit at 8 Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x

Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134

∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Class 8 Maths Practice Set 12.2 Question 9.
A cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Let the number of runs required by the cricket player to score in the third match be x.
Number of runs scored by the player in first match = 180
Number of runs scored in second match = 257
∴ Total runs scored by the player = 180 + 257 + x = 437 + x
Average of runs in the three matches = \(\frac { 437+x }{ 3 }\)
Since, the average of runs should be 230.
\(\frac { 437+x }{ 3 }=230\)
∴ 437 + x = 230 × 3
∴ 437 + x = 690
∴ x = 690 – 437
∴ x = 253
∴ The cricket player should score 253 runs in the third match.

8th Class Math Practice Set 12.2 Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
∴ Anil’s present age = \(\left(\frac{3 x+5}{2}\right)\) years
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.

∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = \(\frac { 15 }{ 3 }\)
∴ x = 5
∴ Viru’s present age is 5 years.

Maharashtra Board Class 8 Maths Chapter 12 Equations in One Variable Practice Set 12.2 Intext Questions and Activities

8th Math Practice Set 12.2 Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.3 8th Std Maths Answers Solutions Chapter 11 Statistics.

Practice Set 11.3 8th Std Maths Answers Chapter 11 Statistics

Exercise 11.3 Class 8 Question 1.
Show the following information by a percentage bar graph.

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75

Solution:

Division of standard 8	A	B	C	D
Number of students securing grade A	45	33	10	15
Total number of students	60	55	40	75
Percentage of students securing grade A	75%	60%	25%	20%
Percentage of students not securing grade A	25%	40%	75%	80%

Statistics for Class 8 Question 2.
Observe the following graph and answer the questions.

1. State the type of the bar graph.
2. How much percent is the Tur production to total production in Ajita’s farm?
3. Compare the production of Gram in the farms of Yash and Ravi and state whose percentage of production is more and by how much?
4. Whose percentage production of Tur is the least?
5. State production percentages of Tur and Gram in Sudha’s farm.

Solution:

1. The given graph is a percentage bar graph.
2. Percent of tur production to the total production in Ajita’s farm is 60%.
3. Production of Gram in the farm of Yash = 50%
   Production of Gram in the farm of Ravi = 30%
   ∴ Difference in the production = 50% – 30% =20%
   ∴ Yash’s production of Gram is more and by 20%.
4. Sudha’s percentage production of Tur is the least.
5. Production percentages of Tur and Gram in Sudha’s farm are 40% and 60% respectively.

8th Standard Statistics Question 3.
The following data is collected in a survey of some students of 10th standard from some schools. Draw the percentage bar graph of the data.

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24

Solution:

School	1st	2nd	3rd	4th
Inclination towards science stream	90	60	25	16
Inclination towards commerce stream	60	20	25	24
Total number of students	150	80	50	40
Percentage of students having inclination towards science stream	60%	75%	50%	40%
Percentage of students having inclination towards commerce stream	40%	25%	50%	60%

Maharashtra Board Class 8 Maths Chapter 11 Statistics Practice Set 11.3 Intext Questions and Activities

Statistics 8th Class Question 1.
Compare and discuss a percentage bar diagram and a subdivided bar diagram. Use it to learn the graphs in the subjects like Science, Geography. (Textbook pg, no. 74)
Solution:
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Miscellaneous Exercise 2 8th Std Maths Answers Solutions.

Miscellaneous Exercise 2 8th Std Maths Answers

Question 1.
Questions and their alternative answers are given. Choose the correct alternative answer.
i. Find the circumference of a circle whose area is 1386 cm²? [Chapter 15]
(A) 132 cm²
(B) 132 cm
(C) 42 cm
(D) 21 cm²
Solution:
(B) 132 cm

Hint:
i. Area of the circle = πr²
1386 = \(\frac { 22 }{ 7 }\) x r²
r² = 1386 x \(\frac { 7 }{ 22 }\)
= 63 x 7
= 441
r = √441 … [Taking square root of both sides]
= 21 cm
Circumference of the circle = 2πr
= 2 x \(\frac { 22 }{ 7 }\) x 21
= 132 cm

ii. The side of a cube is 4 m. If it is doubled, how many times will be the volume of the new cube, as compared with the original cube? [Chapter 16]
(A) Two times
(B) Three times
(C) Four times
(D) Eight times
Solution:
(D) Eight times

Hint:
ii. Original volume = (4)³ = 64 cu.m
New side = 8 m
∴ New volume = (8)² = 512 cu.m
Now, \(\frac{\text { new volume }}{\text { original volume }}=\frac{512}{64}\) = 8
original volume 64
∴ volume of new cube will increase 8 times as compared to the volume of original cube.

Question 2.
Pranalee was practicing for a 100 m running race. She ran 100 m distance 20 times. The time required, in seconds, for each attempt was as follows. [Chapter 11]
18, 17, 17, 16,15, 16, 15, 14,16, 15, 15, 17, 15, 16,15, 17, 16, 15, 14,15
Find the mean of the time taken for running.
Solution:

∴ The mean of the time taken for running 100 m race is 15.7 seconds.

Question 3.
∆DEF and ∆LMN are congruent in the correspondence EDF ↔ LMN. Write the pairs of congruent sides and congruent angles in the correspondence. [Chapter 13]
Solution:

∆EDF ≅ ∆LMN
∴side ED ≅ side LM
side DF ≅ side MN
side EF ≅ side LN
∠E ≅∠L
∠D ≅∠M
∠F ≅∠N

Question 4.
The cost of a machine is Rs 2,50,000. It depreciates at the rate of 4% per annum. Find the cost of the machine after three years. [Chapter 14]
Solution:
Here, P = Cost of the machine = Rs 2,50,000
R = Rate of depreciation = 4%
N = 3 Years
A = Depreciated price of the machine

∴The cost of the machine after three years will be Rs 2,21,184.

Question 5.
In ☐ABCD, side AB || side DC, seg AE ⊥ seg DC. If l(AB) = 9 cm, l(AE) = 10 cm, A(☐ABCD) = 115 cm² , find l(DC). [Chapter 15]
Solution:
Given, side AB || side DC.
∴ ☐ABCD is a trapezium.

Given, l(AB) = 9 cm, l(AE) = 10 cm,
A(☐ABCD) = 115 cm²
Area of a trapezium
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
∴ A(☐ABCD) = \(\frac { 1 }{ 2 }\) x [l(AB) + l(DC) x l(AE)]
∴ 115 = \(\frac { 1 }{ 2 }\) x [9 + l(DC)] x 10
∴ \(\frac { 115 \times 2 }{ 10 }\) = 9 + l(DC)
∴ 23 = 9 + l(DC)
∴ l(DC) = 23 – 9
∴ l(DC) = 14cm

Question 6.
The diameter and height of a cylindrical tank is 1.75 m and 3.2 m respectively. How much is the capacity of tank in litre?
[π = \(\frac { 22 }{ 7 }\)] [Chapter 16]
Solution:
Given: For cylindrical tank:
diameter (d) = 1.75 m, height (h) = 3.2 m
To Find: Capacity of tank in litre
diameter (d) = 1.75 m
= 1.75 x 100
….[∵ 1 m = 100cm]
= 175 cm
∴ radius (r) = \(=\frac{\mathrm{d}}{2}=\frac{175}{2}\) cm
h = 3.2 cm
= 3.2 x 100
= 320 cm
Capacity of tank = Volume of the cylindrical tank
= πr²h

∴ The capacity of the tank is 7700 litre.

Question 7.
The length of a chord of a circle is 16.8 cm, radius is 9.1 cm. Find its distance from the centre. [Chapter 17]
Solution:

Let CD be the chord of the Circle with centre O.
Draw seg OP ⊥ chord CD
∴l(PD) = \(\frac { 1 }{ 2 }\) l(CD)
…[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(PD) = \(\frac { 1 }{ 2 }\) x 16.8 …[l(CD) = 16.8cm]
∴l(PD) = 8.4 cm …(i)
∴In ∆OPD, m∠OPD = 90°
∴[l(OD)]² = [l(OP)]² + [l(PD)]² …..[Pythagoras theorem]
∴(9.1)² = [l(OP)]² + (8.4)² … [From (i) and l(OD) = 9.1 cm]
∴(9.1)² – (8.4)² = [l(OP)]²
∴(9.1 + 8.4) (9.1 – 8.4) = [l(OP)]²
…[∵ a² – b² = (a + b) (a – b)]
∴17.5 x (0.7) = [l(OP)]²
∴12.25 = [l(OP)]²
i.e., [l(OP)]² = 12.25
∴l(OP) = √12.25
…[Taking square root of both sides]
∴l(OP) = 3.5 cm
∴The distance of the chord from the centre is 3.5 cm.

Question 8.
The following tables shows the number of male and female workers, under employment guarantee scheme, in villages A, B, C and D.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110

i. Show the information by a sub-divided bar-diagram.
ii. Show the information by a percentage bar diagram. [Chapter 11]
Solution:
i.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250

ii.

Villages	A	B	C	D
No. of females	150	240	90	140
No. of males	225	160	210	110
Total	375	400	300	250
Percentage of females	40%	60%	30%	56%
Percentage of males	60%	40%	70%	44%

Question 9.
Solve the following equations.
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
iii. 5(1 – 2x) = 9(1 -x)
[Chapter 12]
Solution:
i. 17 (x + 4) + 8 (x + 6) = 11 (x + 5) + 15 (x + 3)
∴ 17x + 68 + 8x + 48 = 11x + 55 + 15x + 45
∴ 17x + 8x + 68 + 48 = 11x + 15x + 55 + 45
∴ 25x + 116 = 26x + 100
∴ 25x + 116 – 116 = 26x + 100 – 116
… [Subtracting 116 from both the sides]
∴ 25x = 26x – 16
∴ 25x – 26x = 26x – 16 – 26x
… [Subtracting 26x from both the sides]
∴ -x = -16
∴ \(\frac{-x}{-1}=\frac{-16}{-1}\)
∴ x = 16

ii. \(\frac{3 y}{2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{3 y \times 2}{2 \times 2}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4}+\frac{y+4}{4}=5-\frac{y-2}{4}\)
∴ \(\frac{6 y}{4} \times 4+\frac{y+4}{4} \times 4=5 \times 4-\frac{y-2}{4} \times 4\)
……[Multiplying both the sides by 4]
∴ 6y + y + 4 = 20 – (y – 2)
∴ 7y + 4 = 20 – y + 2
∴ 7y + 4 = 22 – y
∴ 7y + 4 – 4 = 22 – y – 4
…..[Subtracting 4 from both the sides]
∴ 7y = 18 – y
∴ 7y + y = 18 – y + y
…[Adding y on both the sides]
∴ 8y = 18
∴ \(\frac{8 y}{8}=\frac{18}{8}\) … [Dividing both the sides by 8]
∴ \(y=\frac { 9 }{ 4 }\)

iii. 5(1 – 2x) = 9(1 – x)
∴ 5 – 10x = 9 – 9x
∴ 5 – 10x – 5 = 9 – 9x – 5
….[Subtracting 5 from both the sides]
∴ -10x = 4 – 9x
∴ -10x + 9x = 4 – 9x + 9x
… [Adding 9x on both the sides]
∴ -x = 4
∴ -x x (- 1) = 4 x (- 1)
… [Multiplying both the sides by – 1]
∴ x = – 4

Question 10.
Complete the activity according to the given steps.
i. Draw rhombus ABCD. Draw diagonal AC.
ii. Show the congruent parts in the figure by identical marks.
iii. State by which, test and in which correspondence ∆ADC and ∆ABC are congruent.
iv. Give reason to show ∠DCA ≅ ∠BCA, and ∠DAC ≅ ∠BAC
v. State which property of a rhombus is revealed from the above steps. [Chapter 13]
Solution:
a.

b. In ∆ADC and ∆ABC,
side AD ≅ side AB …..[Sides of a rhombus]
side DC ≅ side BC …..[Sides of a rhombus]
side AC ≅ side AC … [Common side]
∆ADC ≅ ∆ABC … [By SSS test]
∠DCA ≅ ∠BCA …[Corresponding angles of congruent triangles]
∠DAC ≅ ∠BAC …[Corresponding angles of congruent triangles]
From the above steps, property of rhombus revealed is ‘diagonal of a rhombus bisect the opposite angles’.

Question 11.
The shape of a farm is a quadrilateral. Measurements taken of the farm, by naming its corners as P, Q, R, S in order are as follows. l(PQ) = 170 m,
l(QR) = 250 m, l(RS) = 100 m, l(PS) = 240 m, l(PR) = 260 m.
Find the area of the field in hectare (1 hectare = 10,000 sq.m). [Chapter 15]
Solution:

Area of the field = A(∆PQR) + A(∆PSR)
In ∆PQR, a = 170 m, b = 250 m, c = 260 m
Semiperimeter of ∆PQR = s

Area of the field = A(∆PQR) + A(∆PSR)
= 20400 + 12000
= 32400 sq.m
= \(\frac { 32400 }{ 10000 }\)
…[1 hectare = 10,000 sq.m]
= 3.24 hectares
∴ The area of the field is 3.24 hectares.

Question 12.
In a library, 50% of total number of books is of Marathi. The books of English are \(\frac { 1 }{ 3 }\) of Marathi books. The books on Mathematics are 25% of the English books. The remaining 560 books are of other subjects. What is the total number of books in the library? [Chapter 12]
Solution:
Let the total number of books in the library be x
50% of total number of books is of Marathi.
Number of Marathi books = 50% of x
= \(\frac { 50 }{ 100 }x\)
= \(\frac { x }{ 2 }\)
The books of English are \(\frac { 1 }{ 3 }\) of Marathi books.
Number of books of English = \(\frac{1}{3} \times \frac{x}{2}\)
= \(\frac { x }{ 6 }\)
The books on Mathematics are 25% of the English books.
Number of books of Mathematics
= 25% of \(\frac { x }{ 6 }\)
= \(\frac{25}{100} \times \frac{x}{6}\)
= \(\frac { x }{ 24 }\)
Since, there are 560 books of other subjects, the total number of books in the library are


∴ 24x – 17x = 17x + 13440 – 17x
∴ 7x = 13440
∴ \(\frac{7 x}{7}=\frac{13440}{7}\)
∴ x = 1920
∴ The total number of books in the library are 1920.

Question 13.
Divide the polynomial (6x³ + 11x² – 10x – 7) by the binomial (2x + 1). Write the quotient and the remainder. [Chapter 10]
Solution:

∴ Quotient = 3x² + 4x – 7,
remainder = 0
Explanation:

Maharashtra Board Class 8 Maths Solutions

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.5 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Yield of soyabean per acre in quintal in Mukund’s field for 7 years was 10, 7, 5,3, 9, 6, 9. Find the mean of yield per acre.
Solution:

Mean = 7
The mean of yield per acre is 7 quintals.

Question 2.
Find the median of the observations, 59, 75, 68, 70, 74, 75, 80.
Solution:
Given data in ascending order:
59, 68, 70, 74, 75, 75, 80
∴ Number of observations(n) = 7 (i.e., odd)
∴ Median is the middle most observation
Here, 4th number is at the middle position, which is = 74
∴ The median of the given data is 74.

Question 3.
The marks (out of 100) obtained by 7 students in Mathematics examination are given below. Find the mode for these marks.
99, 100, 95, 100, 100, 60, 90
Solution:
Given data in ascending order:
60, 90, 95, 99, 100, 100, 100
Here, the observation repeated maximum number of times = 100
∴ The mode of the given data is 100.

Question 4.
The monthly salaries in rupees of 30 workers in a factory are given below.
5000, 7000, 3000, 4000, 4000, 3000, 3000,
3000, 8000, 4000, 4000, 9000, 3000, 5000,
5000, 4000, 4000, 3000, 5000, 5000, 6000,
8000, 3000, 3000, 6000, 7000, 7000, 6000,
6000, 4000
From the above data find the mean of monthly salary.
Solution:

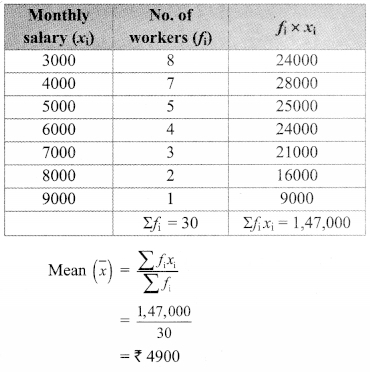
∴ The mean of monthly salary is ₹ 4900.

Question 5.
In a basket there are 10 tomatoes. The weight of each of these tomatoes in grams is as follows:
60, 70, 90, 95, 50, 65, 70, 80, 85, 95.
Find the median of the weights of tomatoes.
Solution:
Given data in ascending order:
50, 60, 65, 70, 70, 80 85, 90, 95, 95
∴ Number of observations (n) = 10 (i.e., even)
∴ Median is the average of middle two observations
Here, 5th and 6th numbers are in the middle position
∴ Median = \(\frac { 70+80 }{ 2 }\)
∴ Median = \(\frac { 150 }{ 2 }\)
∴ The median of the weights of tomatoes is 75 grams.

Question 6.
A hockey player has scored following number of goals in 9 matches: 5, 4, 0, 2, 2, 4, 4, 3,3.
Find the mean, median and mode of the data.
Solution:
i. Given data: 5, 4, 0, 2, 2, 4, 4, 3, 3.
Total number of observations = 9


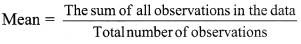
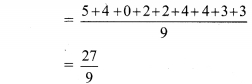
∴ The mean of the given data is 3.

ii. Given data in ascending order:
0,2, 2, 3, 3, 4, 4, 4,5
∴ Number of observations(n) = 9 (i.e., odd)
∴ Median is the middle most observation
Here, the 5^th number is at the middle position, which is 3.
∴ The median of the given data is 3.

iii. Given data in ascending order:
0,2, 2, 3, 3, 4, 4, 4,5
Here, the observation repeated maximum number of times = 4
∴ The mode of the given data is 4.

Question 7.
The calculated mean of 50 observations was 80. It was later discovered that observation 19 was recorded by mistake as 91. What Was the correct mean?
Solution:
Here, mean = 80, number of observations = 50
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations
∴ The sum of 50 observations = 80 x 50
= 4000
One of the observation was 19. However, by mistake it was recorded as 91.
Sum of observations after correction = sum of 50 observation + correct observation – incorrect observation
= 4000 + 19 – 91
= 3928
∴ Corrected mean

= 78.56
∴ The corrected mean is 78.56.

Question 8.
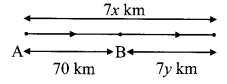
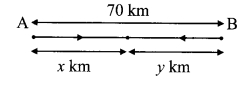
Following 10 observations are arranged in ascending order as follows. 2, 3 , 5 , 9, x + 1, x + 3, 14, 16, 19, 20. If the median of the data is 11, find the value of x.
Solution:
Given data in ascending order :
2, 3, 5, 9, x + 1, x + 3, 14, 16, 19, 20.
∴ Number if observations (n) = 10 (i.e., even)
∴ Median is the average of middle two observations
Here, the 5th and 6th numbers are in the middle position.
∴ \( \text { Median }=\frac{(x+1)+(x+3)}{2}\)
∴ 11 = \(\frac { 2x+4 }{ 2 }\)
∴ 22 = 2x + 4
∴ 22 – 4 = 2x
∴ 18 = 2x
∴ x = 9

Question 9.
The mean of 35 observations is 20, out of which mean of first 18 observations is 15 and mean of last 18 observations is 25. Find the 18th observation.
Solution:
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations
= Mean x Total number of observations
The mean of 35 observations is 20
∴ Sum of 35 observations = 20 x 35 = 700 ,..(i)
The mean of first 18 observations is 15
Sum of first 18 observations =15 x 18
= 270 …(ii)
The mean of last 18 observations is 25 Sum of last 18 observations = 25 x 18
= 450 …(iii)
∴ 18^th observation = (Sum of first 18 observations + Sum of last 18 observations) – (Sum of 35 observations)
= (270 + 450) – (700) … [From (i), (ii) and (iii)]
= 720 – 700 = 20
The 18^th observation is 20.

Question 10.
The mean of 5 observations is 50. One of the observations was removed from the data, hence the mean became 45. Find the observation which was removed.
Solution:
\( \text { Mean }=\frac{\text { The sum of all observations }}{\text { Total number of observations }}\)
∴ The sum of all observations = Mean x Total number of observations
The mean of 5 observations is 50
Sum of 5 observations = 50 x 5 = 250 …(i)
One observation was removed and mean of remaining data is 45.
Total number of observations after removing one observation = 5 – 1 = 4
Now, mean of 4 observations is 45.
∴ Sum of 4 observations = 45 x 4 = 180 …(ii)
∴ Observation which was removed
= Sum of 5 observations – Sum of 4 observations = 250 – 180 … [From (i) and (ii)]
= 70
∴ The observation which was removed is 70.

Question 11.
There are 40 students in a class, out of them 15 are boys. The mean of marks obtained by boys is 33 and that for girls is 35. Find out the mean of all students in the class.
Solution:
Total number of students = 40
Number of boys =15
∴ Number of girls = 40 – 15 = 25
The mean of marks obtained by 15 boys is 33
Here, sum of the marks obtained by boys
= 33 x 15
= 495 …(i)
The mean of marks obtained by 25 girls is 35 Sum of the marks obtained by girls = 35 x 25
= 875 …(ii)
Sum of the marks obtained by boys and girls = 495 + 875 … [From (i) and (ii)]
= 1370
∴ Mean of all the students

= 34.25
∴ The mean of all the students in the class is 34.25.

Question 12.
The weights of 10 students (in kg) are given below:
40, 35, 42, 43, 37, 35, 37, 37, 42, 37. Find the mode of the data.
Solution:
Given data in ascending order:
35, 35, 37, 37, 37, 37, 40, 42, 42, 43
∴ The observation repeated maximum number of times = 37
∴ Mode of the given data is 37 kg

Question 13.
In the following table, the information is given about the number of families and the siblings in the families less than 14 years of age. Find the mode of the data.

Solution:
Here, the maximum frequency is 25.
Since, Mode = observations having maximum frequency
∴ The mode of the given data is 2.

Question 14.
Find the mode of the following data.

Solution:
Here, the maximum frequency is 9.
Since, Mode = observations having maximum frequency
But, this is the frequency of two observations.
∴ Mode = 35 and 37

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.5 Intext Questions and Activities

Question 1.
The first unit test of 40 marks was conducted for a class of 35 students. The marks obtained by the students were as follows. Find the mean of the marks.
40, 35, 30, 25, 23, 20, 14, 15, 16, 20, 17, 37, 37, 20, 36, 16, 30, 25, 25, 36, 37, 39, 39, 40, 15, 16, 17, 30, 16, 39, 40, 35, 37, 23, 16.
(Textbook pg, no. 123)
Solution:
Here, we can add all observations, but it will be a tedious job. It is easy to make frequency distribution table to calculate mean.

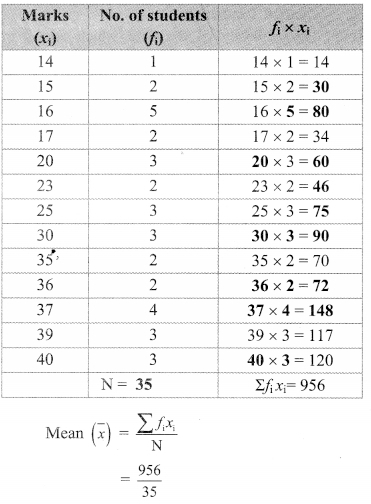
= 27.31 marks (approximately)
∴ The mean of the mark is 27.31.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 7 Statistics.

Practice Set 7.4 Algebra 9th Std Maths Part 1 Answers Chapter 7 Statistics

Question 1.
Complete the following cumulative frequency table:

Solution:

Question 2.
Complete the following Cumulative Frequency Table:

Solution:

Question 3.
The data is given for 62 students in a certain class regarding their mathematics marks out of 100. Take the classes 0 – 10, 10 – 20,… and prepare frequency distribution
table and cumulative frequency table more than or equal to type.
55. 60, 81, 90, 45, 65, 45, 52, 30, 85, 20, 10,
75, 95, 09, 20, 25, 39, 45, 50, 78, 70, 46, 64,
42. 58. 31, 82, 27, 11, 78, 97, 07, 22, 27, 36,
35, 40, 75, 80, 47, 69, 48, 59, 32, 83, 23, 17,
77, 45, 05, 23, 37, 38, 35, 25, 46, 57, 68, 45.
47,49
From the prcparcd table, answer the following questions :
i. How many students obtained marks 40 or above 40?
ii. How many students obtained marks 90 or above 90?
iii. How many students obtained marks 60 or above 60?
iv. What is the cumulative frequency of equal to or more than type of the class 0 – 10?
Solution:

i. 38 students obtained marks 40 or above 40.
ii. 3 students obtained marks 90 or above 90.
iii. 19 students obtained marks 60 or above 60.
iv. Cumulative frequency of equal to or more than type of the class 0 – 10 is 62.

Question 4.
Using the data In example (3) above, prepare less than type cumulative frequency table and answer the following questions.
i. How many students obtained less than 40 marks?
ii. How many students obtained less than 10 marks?
iii. How many students obtained less than 60 marks?
iv. Find the cumulative frequency of the class 50 – 60.
Solution:

i. 24 students obtained less than 40 marks.
ii. 3 students obtained less than 10 marks.
iii. 43 students obtained less than 60 marks.
iv. Cumulative frequency of the class 50 – 60 is 43.

Maharashtra Board Class 9 Maths Chapter 7 Statistics Practice Set 7.4 Intext Questions and Activities

Question 1.
The following information is regarding marks in mathematics, obtained out of 40, scored by 50 students of 9th std. ¡n the first unit test. (Textbook pg. no. 120)

From the table, fill in the blanks in the following statements.
i. For class interval 10 – 20 the lower class limit is _____ and upper class limit is _____
ii. How many students obtained marks less than 10? 2
iii. How many students obtained marks less than 20? 2 + ____ = 14
iv. How many students obtained marks less than 30? ______ + _____ = 34
v. How many students obtained marks less than 40? ______ + ______ =50
Solution:
i. 10, 20
iii. 12
iv. 14 + 20
v. 34 + 16

Question 2.
A sports club has organised a table-tennis tournaments. The following table gives the distribution of players ages. Find the cumulative frequencies equal to or more than the lower class limit and complete the table (Textbook pg. no. 121)
Solution:
Equal to lower limit or more than lower limit type of cumulative table.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.

Problem Set 5 Algebra 9th Std Maths Part 1 Answers Chapter 5 Linear Equations in Two Variables

Question 1.
Choose the correct alternative answers for the following questions.

i. If 3x + 5y = 9 and 5x + 3y = 7, then what is the value of x + y ?
(A) 2
(B) 16
(C) 9
(D) 7
Answer:
(A) 2

ii. ‘When 5 is subtracted from length and breadth of the rectangle, the perimeter becomes 26’. What is the mathematical form of the statement ?
(A) x – y = 8
(B) x + y = 8
(C) x + y = 23
(D) 2x + y = 21
Answer:
(C) x + y = 23

iii. Ajay is younger than Vijay by 5 years. Sum of their ages is 25 years. What is Ajay’s age?
(A) 20 years
(B) 15 years
(C) 10 years
(D) 5 years
Answer:
(C) 10 years

Hints:
i. Adding the given equations,
3x+ 5y = 9
5x + 3y = 7
8x + 8y = 16
∴ x + y = 2 .. [Dividing both sides by 8]

ii. Let the length of the rectangle be ‘x’ and that of breadth be ‘y’.
Perimeter of rectangle = 2[(x – 5) + (y – 5)]
∴ 26 = 2(x + y – 10)
∴ x + y – 10 = 13
∴ x + y = 23

iii. Let the age of Ajay bex years.
∴ x + (x + 5) = 25
∴ 2x = 20
∴ x = 10 years

Question 2.
Solve the following simultaneous equations.
i. 2x + y = 5 ; 3x – y = 5
ii. x – 2y = -1 ; 2x – y = 7
iii. x + y = 11 ; 2x – 3y = 7
iv. 2x + y = -2 ; 3x – y = 7
V. 2x – y = 5 ; 3x + 2y = 11
vi. x – 2y – 2 ; x + 2y = 10
Solution:
ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = 10/5
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.

ii. x – 2y = -1
∴x = 2y – 1 … .(i)
∴ 2x – y = 7 ….(ii)
Substituting x = 2y – 1 in equation (ii),
2(2y – 1) – y = 7
∴ 4y – 2 – y = 7
∴ 3y = 7 + 2
∴ 3y = 9
∴ y = 9/3
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y – 1
∴ x = 2(3) – 1
∴ x = 6 – 1 = 5
∴ (5, 3) is the solution of the given equations.

iii. x + y = 11
∴ x = 11 – y …(i)
2x – 3y = 7 …….(ii)
Substituting x = 11 -y in equation (ii),
2(11 – y) – 3y = 7
∴ 22 – 2y – 3y = 1
∴ 22 – 5y = 7
∴ 22 – 7 = 5y
∴ 15 = 5y
∴ y = \(\frac { 15 }{ 5 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 11 – y
∴ x = 11 – 3 = 8
∴ (8, 3) is the solution of the given equations.

iv. 2x + y = -2 …(i)
3x – y = 7 …(ii)
Adding equations (i) and (ii),
2x + y = -2
+ 3x – y = l
5x = 5
∴ x = \(\frac { 5 }{ 5 }\)
∴ x = 1
Substituting x = 1 in equation (i),
2x + y = -2
∴ 2(1) +y = -2
2 + y = -2
∴ y = – 2 – 2
∴ y = -4
∴ (1, -4) is the solution of the given equations.

v. 2x – y = 5
∴ -y = 5 – 2x
∴ y = 2x – 5 …(i)
3x + 2y = 11 ……(ii)
Substituting y = 2x – 5 in equation (ii),
3x + 2(2x – 5) = 11
∴ 3x + 4x- 10= 11
∴ 7x = 11 + 10
∴ 7x = 21
∴ x = \(\frac { 21 }{ 7 }\)
∴ x = 3
Substituting x = 3 in equation (i),
y = 2x – 5
∴ y = 2(3) – 5
∴ y = 6 – 5 = 1
∴(3,1) is the solution of the given equations.

vi. x – 2y = -2
∴ x = 2y – 2 …(i)
x + 2y = 10 …..(ii)
Substituting x = 2y – 2 in equation (ii),
2y – 2 + 2y = 10
∴ 4y = 10 + 2
∴ 4y= 12
∴ y = \(\frac { 12 }{ 7 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y – 2
∴ x = 2(3) – 2
∴ x = 6 – 2 = 4
∴ (4, 3) is the solution of the given equations.

Question 3.
By equating coefficients of variables, solve the following equations. [3 Marks each]
i. 3x – 4y = 7 ; 5x + 2y = 3
ii. 5x + ly= 17 ; 3x – 2y = 4
iii. x – 2y = -10 ; 3x – 3y = -12
iv. 4x+y = 34 ; x + 4y = 16
Solution:
i. 3x – 4y = 7 …(i)
5x + 2y = 3 ….(ii)
Multiplying equation (ii) by 2,
10x + 4y = 6 …(iii)
Adding equations (i) and (iii),

∴ x = 1
Substituting x = 1 in equation (i),
3x – 4y = 7
∴ 3(1) – 4y = 7
∴ 3 – 4y = 7
∴ 3 – 7 = 4y
∴ -4 = 4y
∴ y = \(\frac { -4 }{ 4 }\)
∴ y = -1
∴ (1, -1) is the solution of the given equations.

ii. 5x + 7y = 17 …(i)
3x – 2y = 4 ….(ii)
Multiplying equation (i) by 2,
10x + 14y = 34 …(iii)
Multiplying equation (ii) by 7,
21x – 14y = 28 …..(iv)
Adding equations (iii) and (iv),

∴ x = 2
Substituting x = 2 in equation (ii),
3x – 2y = 4
∴ 3(2) – 2y = 4
∴ 6 – 2y = 4
∴ 6 – 4 = 2y
∴ 2 = 2y
∴ y = \(\frac { 2 }{ 2 }\)
∴ y = 1
∴ (2,1) is the solution of the given equations.

iii. x – 2y = -10 ….(i)
3x – 5y = -12 …….(ii)
Multiplying equation (i) by 3,
3x – 6y = -30 …(iii)
Subtracting equation (ii) from (iii),

∴ y = 18
Substituting y = 18 in equation (i),
x – 2y = -10
∴ x – 2(18) = -10
∴ x – 36 = -10
∴ x = -10 + 36 = 26
∴ (26, 18) is the solution of the given equations.

iv. 4x + y = 34 …(i)
x + 4y = 16 …… (ii)
Multiplying equation (i) by 4,
16x + 4y = 136 …(iii)
Subtracting equation (ii) from (iii),

x = 8
Substituting x = 8 in equation (i),
4x + y = 34
∴ 4(8) + y = 34
∴ 32 + y = 34
∴ y = 34 – 32 = 2
∴ (8, 2) is the solution of the given equations.

Question 4.
Solve the following simultaneous equations.

Solution:
i. \(\frac{x}{3}+\frac{y}{4}=4\)
Multiplying both sides by 12,
4x + 3y = 48 …(i)
\(\frac{x}{2}-\frac{y}{4}=1\)
Multiplying both sides by 8,
4x – 2y = 8 …..(ii)
Subtracting equation (ii) from (i),

∴ y = 8
Substituting y = 8 in equation (ii),
4x – 2y = 8
∴ 4x – 2(8) = 8
∴ 4x – 16 = 8
∴ 4x = 8+ 16
∴ 4x = 24
∴ x = \(\frac { 24 }{ 4 }\)
∴ x = 6
∴ (6, 8) is the solution of the given equations.

ii. \(\frac { x }{ 3 }\) + 5y = 13
Multiplying both sides by 3,
x + 15y = 39 …(i)
2x + \(\frac { y }{ 2 }\) =19
Multiplying both sides by 2,
4x + y = 38 …….(ii)
Multiplying equation (i) by 4,
4x + 60y = 156 …(iii)
Subtracting equation (ii) from (iii),
4x + 60y =156 4x + y= 38

∴ y = 2
Substituting y = 2 in equation (i),
x + 15y = 39
∴ x+ 15(2) = 39
∴ x + 30 = 39
∴ x = 39 – 30 = 9
∴ (9,2) is the solution of the given equations.

iii. \(\frac { 2 }{ x }\) + \(\frac { 3 }{ y }\) = 13
Multiplying both sides by 5,

Question 5.
A two digit number is 3 more than 4 times the sum of its digits. If 18 is added to this number, the sum is equal to the number obtained by interchanging the digits. Find the number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the first condition,
a two digit number is 3 more than 4 times the sum of its digits.
10y + x = 4(x + y) + 3
∴ 10y + x = 4x + 4y + 3
∴ x – 4x + 10y – 4y = 3
∴ – 3x + 6y = 3
Dividing both sides by -3,
x – 2y = -1 …(i)
According to the second condition,
if 18 is added to the number, the sum is equal to the number obtained by interchanging the digits.
10y + x + 18= 10x + y
∴ x – 10x + 10y – y = -18
∴ – 9x + 9y = -18
Dividing both sides by – 9,
x – y = 2 ……(ii)
Subtracting equation (ii) from (i),

∴ y = 3
Substituting y = 3 in equation (ii),
x – y = 2
∴ x – 3 = 2
∴ x = 2 + 3 = 5
∴ Original number = 10y + x
= 10(3) + 5
= 30 + 5
= 35
The required number is 35.

Question 6.
The total cost of 8 books and 5 pens is ₹ 420 and the total cost of 5 books and 8 pens is ₹321. Find the cost of 1 book and 2 pens.
Solution:
Let the cost of one book be ₹ x and the cost of one pen be ₹ y.
According to the first condition,
the total cost of 8 books and 5 pens is ₹ 420.
∴ 8x + 5y = 420 …(i)
According to the second condition, the total cost of 5 books and 8 pens is ₹ 321.
5x + 8y = 321 ….(ii)
Multiplying equation (i) by 5,
40x + 25y = 2100 …(iii)
Multiplying equation (ii) by 8,
40x + 64y = 2568 … (iv)
Subtracting equation (iii) from (iv),

∴ y = 12
Substituting y = 12 in equation (i),
8x + 5y = 420
∴ 8x + 5(12) = 420
∴ 8x + 60 = 420
∴ 8x = 420 – 60
∴ 8x = 360
∴ x = \(\frac { 360 }{ 8 }\)
∴ x = 45
Cost of 1 book and 2 pens = x + 2y
= 45 + 2(12)
= 45 + 24
= ₹69
∴ The cost of 1 book and 2 pens is ₹69.

Question 7.
The ratio of incomes of two persons is 9 : 7. The ratio of their expenses is 4 : 3. Every person saves ₹ 200, find the income of each.
Solution:
Let the income of first person be ₹ x and that of second person be ₹ y.
According to the first condition,
the ratio of their incomes is 9 : 7.
∴ \(\frac { x }{ y }\) = \(\frac { 9 }{ 7 }\)
∴ 7x = 9y
∴ 7x – 9y = 0 …….(i)
Each person saves ₹ 200.
Expenses of first person = Income – Saving = x – 200
Expenses of second person = y – 200
According to the second condition,
the ratio of their expenses is 4 : 3
∴ \(\frac { x – 200 }{ y – 200 }\) = \(\frac { 4 }{ 3 }\)
∴ 3(x – 200) = 4(y – 200)
∴ 3x – 600 = 4y – 800
∴ 3x – 4y = – 800 + 600
∴ 3x – 4y = -200 …(ii)
Multiplying equation (i) by 4,
28x-36y =0 …(iii)
Multiplying equation (ii) by 9,
27x-36y = -1800 …(iv)
Subtracting equation (iv) from (iii),

Substituting x = 1800 in equation (i),
7x – 9y = 0
∴ 7(1800) – 9y = 0
∴ 9y = 7 x 1800
∴ y = \(\frac { 7 \times 1800 }{ 9 }\)
y = 7 x 200
∴ y = 1400
∴ The income of first person is ₹ 1800 and that of second person is ₹ 1400.

Question 8.
If the length of a rectangle is reduced by 5 units and its breadth is increased by 3 units, then the area of the rectangle is reduced by 9 square units. If length is reduced by 3 units and breadth is increased by 2 units, then the area of rectangle will increase by 67 square units. Then find the length and breadth of the rectangle.
Solution:
Let the length of the rectangle be ‘x’ units and the breadth of the rectangle be ‘y’ units.
Area of the rectangle = xy sq. units
length of the rectangle is reduced by 5 units
∴ length = x – 5
breadth of the rectangle is increased by 3 units
∴ breadth = y + 3
area of the rectangle is reduced by 9 square units
∴ area of the rectangle = xy – 9
According to the first condition,
(x – 5)(y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y = -9 + 15
∴ 3x – 5y = 6 …(i)
length of the rectangle is reduced by 3 units
∴ length = x – 3
breadth of the rectangle is increased by 2 units
∴ breadth = y + 2
area of the rectangle is increased by 67 square units
∴ area of the rectangle = xy + 61
According to the second condition,
(x – 3)(y + 2) = xy + 67
∴ xy + 2x – 3y – 6 = xy + 67
∴ 2x – 3y = 67 + 6
∴ 2x – 3y = 73 …(ii)
Multiplying equation (i) by 3,
9x – 15y = 18 . ..(iii)
Multiplying equation (ii) by 5,
10x – 15y = 365 …(iv)
Subtracting equation (iii) from (iv), 10x- 15y= 365 9x-15y= 18

Substituting x = 347 in equation (ii),
2x – 3y = 73
∴ 2(347) – 3y = 73
∴ 694 – 73 = 3y
∴ 621 = 3y
∴ y = \(\frac { 621 }{ 3 }\)
∴ y = 207
∴ The length and breadth of rectangle are 347 units and 207 units respectively.

Question 9.
The distance between two places A and B on a road is 70 kilometres. A car starts from A and the other from B. If they travel in the same direction, they will meet in 7 hours. If they travel towards each other they will meet in 1 hour, then find their speeds.
Solution:
Let the speed of the car starting from A (first car) be ‘x’ km/hr and that starting from B (second car) be ‘y’ km/hr. (x > y)
According to the first condition,
Distance covered by the first car in 7 hours = 7x km
Distance covered by the second car in 7 hours = 7y km

If the cars are travelling in the same direction, 7x – 7y = 70
Dividing both sides by 7,
x – y = 10 …(i)
According to the second condition,
Distance covered by the first car in
1 hour = x km
Distance covered by the second car in 1 hour = y km

If the cars are travelling in the opposite direction
x + y = 70 …(ii)
Adding equations (i) and (ii),

∴ x = 40
Substituting x = 40 in equation (ii), x + y = 70
∴ 40 +y = 70
∴ y = 70 – 40 = 30
∴ The speed of the cars starting from places A and B are 40 km/hr and 30 km/hr respectively.

Question 10.
The sum of a two digit number and the number obtained by interchanging its digits is 99. Find the number.
Solution:
Let the digit in unit’s place be ‘x’ and the digit in ten’s place be ‘y’.

According to the given condition,
the sum of a two digit number and the number
obtained by interchanging its digits is 99.
∴ 10y + x + 10x +y = 99
∴ 11x + 11y = 99
Dividing both sides by 11,
x + y = 9
If y = 1, then x = 8
If y = 2, then x = 7
If y = 3, then x = 6 and so on.
∴ The number can be 18, 27, 36, … etc.

Maharashtra Board Class 9 Maths Chapter 5 Linear Equations in Two Variables Practice Set 5 Intext Questions and Activities

Question 1.
On the glasses of following spectacles, write numbers such that (Textbook pg. no. 82)
i. Their sum is 42 and difference is 16.

ii. Their sum is 37 and difference is 11.

iii. Their sum is 54 and difference is 20.

iv. Their sum is … and difference is … .

Answer:
ii. x + y = 37 and x – y = 11
∴ x = 24, y = 13
iii. x +y = 54 and x – y = 20
∴ x = 37, y =17

Question 2.
There are instructions written near the arrows in the following diagram. From this information form suitable equations and write in the boxes indicated by arrows. Select any two equations from these boxes and find their solutions. Also verify the solutions. By taking one pair of equations at a time, how many pairs can be formed ? Discuss the solutions for these pairs. (Textbook pg. no. 92)

Answer:
Here, if we take a pair of any two equations, we get following 6 pairs.

1. equation (i) and (ii)
2. equation (i) and (iii)
3. equation (i) and (iv)
4. equation (ii) and (iii)
5. equation (ii) and (iv)
6. equation (iii) and (iv)

Solution of each pair given above is (21, 15).
Here, all four equations are of same rectangle. By solving any two equations simultaneously, we get length and breadth of the rectangle.

Question 3.
Find the function.

∴ Given function = \(\frac { 6 }{ 14 }\)
Verify the answer obtained. (Textbook pg. no. 92)
Answer:
For the fraction\(\frac { 6 }{ 14 }\), if the numerator is multiplied by 3 and 3 is subtracted from the denominator, we get fraction \(\frac { 18 }{ 11 }\).
Similarly, for the fraction \(\frac { 6 }{ 14 }\), if the numerator is increased by 8 and the denominator is doubled, we get fraction \(\frac { 1 }{ 2 }\).

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.

Practice Set 6.1 Algebra 9th Std Maths Part 1 Answers Chapter 6 Financial Planning

Question 1.
Alka spends 90% of the money that she receives every month, and saves ₹ 120. How much money does she get monthly?
Solution:
Let Alka’s monthly income be ₹ x.
Alka spends 90% of the money that she receives every month.
∴ Amount spent by Alka = 90% of x
= \(\frac { 90 }{ 100 }\) × x = 0.9x 100
Now, Savings = Income – Expenditure
∴ 120 = x – 0.9x
∴120 = 0.1 x
∴ \(x=\frac{120}{0.1}=\frac{120 \times 10}{0.1 \times 10}\)
∴ x = 1200
Alka gets ₹ 1200 monthly.

Question 2.
Sumit borrowed a capital of ₹ 50,000 to start his food products business. In the first year he suffered a loss of 20%. He invested the remaining capital in a new sweets business and made a profit of 5%. How much was his profit or loss computed on his original capital ?
Solution:
Original capital borrowed by Sumit = ₹ 50000
Sumit suffered a loss of 20% in his food products business.
∴ Loss suffered in the first year = 20% of 50000
= \(\frac { 20 }{ 100 }\) × 50000
= ₹10000
Remaining capital = Original capital – loss suffered = 50000- 10000
= ₹ 40000
Sumit invested the remaining capital i.e. ₹ 40,000 in a new sweets business. He made a profit of 5%.
Profit in sweets business = 5% of 40000
= \(\frac { 5 }{ 100 }\) x 40000 100
= ₹ 2000
New capital with Sumit after the profit in new sweets business = 40000 + 2000 = ₹42000
Since, the new capital is less than the original capital, we can conclude that Sumit suffered a loss.
Total loss on original capital = Original capital – New capital
= 50000 – 42000 = ₹ 8000

∴ Sumit suffered a loss of 16% on the original capital.

Question 3.
Nikhil spent 5% of his monthly income on his children’s education, invested 14% in shares, deposited 3% in a bank and used 40% for his daily expenses. He was left with a balance of ₹ 19,000. What was his income that month?
Solution:
Let the monthly income of Nikhil be ₹ x.
Nikhil invested 14% in shares and deposited 3% in a bank.
∴ Total investment = (14% + 3%) of x
= 17% of x
= \(\frac { 17 }{ 100 }\) × x
= 0.1 7 x
Nikhil spent 5% on his children’s education and used 40% for his daily expenses.

∴ Total expenditure = (5% + 40%) of x
= 45% of x
= \(\frac { 45 }{ 100 }\) × x
= 0.45x
Amount left with Nikhil = 19,000
Amount left with Nikhil = Income – (Total investment + Total expenditure)
∴ 19000 = x – (0.17x + 0.45x)
∴ 19000 = x – 0.62x ,
∴ 19000 = 0.38x
∴ \(x=\frac{19000}{0.38}=\frac{19000 \times 100}{0.38 \times 100}=\frac{1900000}{38}\)
= 50000
∴ The monthly income of Nikhil is ₹ 50000.

Question 4.
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years. Mr. Fernandes invested ₹ 1,20,000 in a mutual fund for 2 years. After 2 years, Mr. Fernandes got ₹ 1,92,000. Whose investment turned out to be more profitable?
Solution:
Mr. Sayyad:
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years P = ₹ 40000, R = 8%, n = 2 years
∴ Compound interest (I)
= Amount (A) – Principal (P)

= 40000 [(1 +0.08)² – 1]
= 40000 [(1.08)² – 1]
= 40000(1.1664 – 1)
= 40000 (0.1664)
= ₹ 6656
∴ Mr. Sayyad’s percentage of profit Interest

Mr. Fernandes:
Amount invested by Mr. Fernandes in mutual fund = ₹ 120000
Amount received by Mr. Fernandes after 2 years = ₹ 192000
∴ Profit earned by Mr. Fernandes
= Amount received – Amount invested
= 192000- 120000
= ₹72000
∴ Mr. Fernandes percentage of profit Profit earned

= 60%
From (i) and (ii),
Investment of Mr. Fernandes turned out to be more profitable.

Question 5.
Sameera spent 90% of her income and donated 3% for socially useful causes. If she was left with ₹ 1750 at the end of the month, what was her actual income ?
Solution:
Let the actual income of Sameera be ₹ x.
Sameera spent 90% of her income and donated 3%.
∴ Sameera’s total expenditure
= (3% + 90%) of x
= 93% of x
= \(\frac { 93 }{ 100 }\) × x
= 0.93x
Now, Savings = Income – Expenditure
∴ 1750 = x-0.93x
∴ 1750 = 0.07x
\(x=\frac{1750}{0.07}=\frac{1750 \times 100}{0.07 \times 100}=\frac{175000}{7}=25000\)
∴ The actual income of Sameera is ₹ 25000.

Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Practice Set 6.1 Intext Questions and Activities

Question 1.
Amita invested some part of ₹ 35000 at 4% and the rest at 5% interest for one year. Altogether her gain was ₹ 1530. Find out the amounts she had invested at the two different rates. Write your answer in words. (Textbook pg. no. 97)
Solution:
Let the amount invested at the rate of 4% and 5% be ₹ x and ₹ y respectively.
According to the first condition, total amount invested = ₹ 35000
∴ x + y = 35000 …(i)
According to the second condition,
total interest received at 4% and 5% is ₹ 1530.
∴ 4 % of x + 5 % of y = 1530
∴ \(\frac { 4 }{ 100 }\) x x + \(\frac { 5 }{ 100 }\) x y = 1530
∴ 4x + 5y = 153000 …(ii)
Multiplying equation (i) by 4, we get
4x + 4y = 140000 …(iii)
Subtracting equation (iii) from (ii),

Substituting y = 13000 in equation (i),
x + 13000 = 35000
∴ x = 35000 – 13000 = 22000

∴ Amita invested ₹ 22000 at the rate of 4% and ₹ 13000 at the rate of 5%.