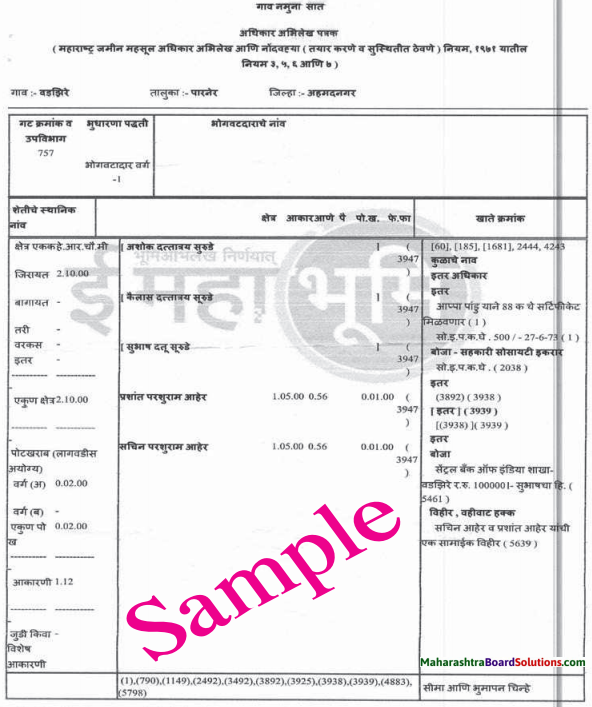
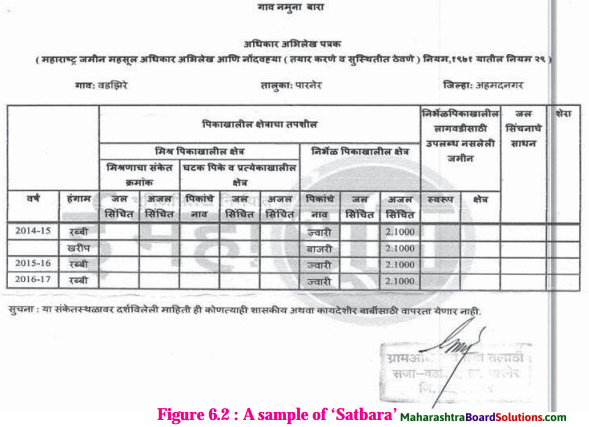
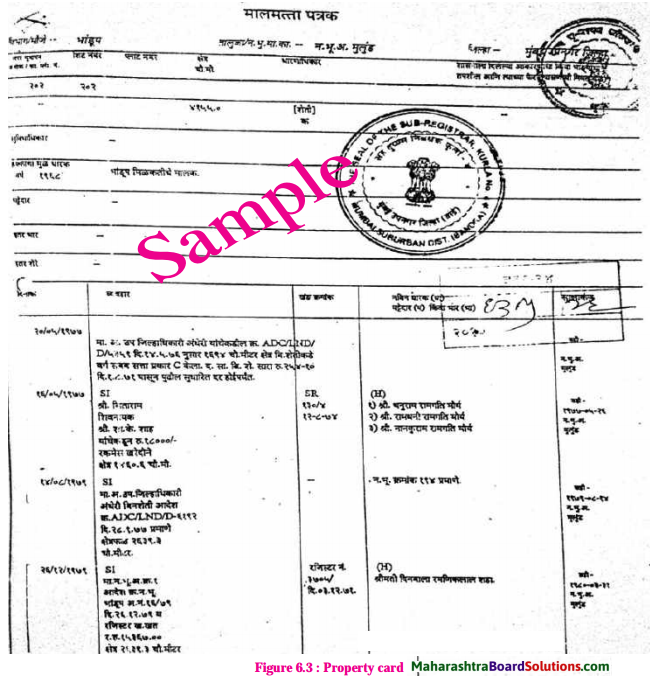
Balbharti Maharashtra State Board Class 8 Science Solutions Chapter 1 Living World and Classification of Microbes Notes, Textbook Exercise Important Questions and Answers.
Std 8 Science Chapter 1 Living World and Classification of Microbes Question Answer Maharashtra Board
Class 8 Science Chapter 1 Living World and Classification of Microbes Question Answer Maharashtra Board
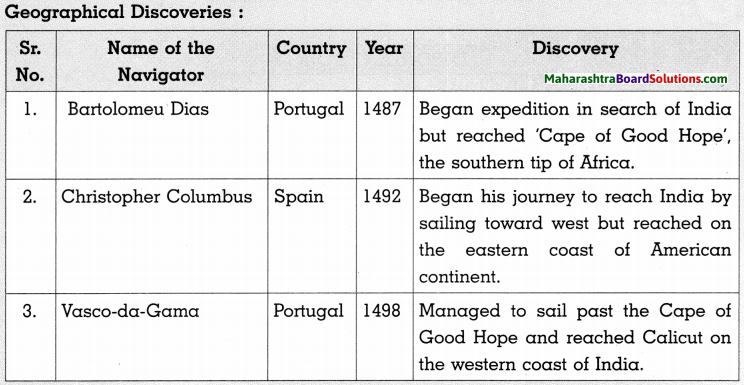
1. Use Whittaker method to classify bacteria, protozoa, fungi, algae, prokaryotic, eukaryotic, microbes.
Living World And Classification Of Microbes Exercises Question 1.
Use Whittaker method to classify bacteria, protozoa, fungi, algae, prokaryotic, eukaryotic, microbes.
Answer:
- Bacteria: Kingdom Monera
- Protozoa: Kingdom Protista
- Fungi: Kingdom Fungi
- Algae: If unicellular, Kingdom Protista. If multicellular, Kingdom Plantae
- Prokaryotic: Kingdom Monera
- Eukaryotic: Any kingdom other than Monera.
- Microbes: Kingdom Monera or Protista.
2. Complete the five kingdom method of classification using-living organism, prokaryotes, eukaryotes, multicellular, unicellular, protista, animals, plants, fungi.
Living World And Classification Of MicrobesQuestion 1.
Complete the five kingdom method of classification using-living organism, prokaryotes, eukaryotes, multicellular, unicellular, protista, animals, plants, fungi.
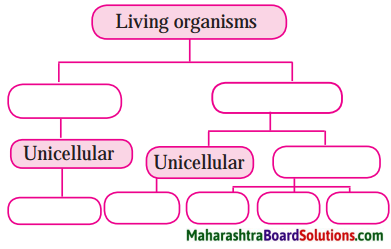
Answer:
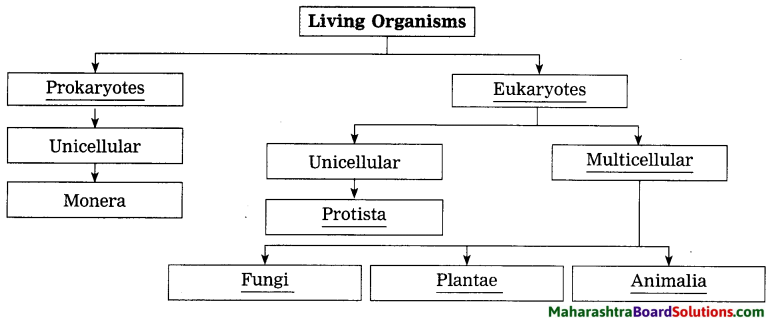
3. Find out my partner
Question 1.
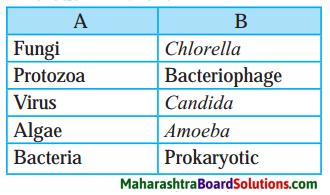
Answer:
| A | B |
| 1. Fungi | Candida |
| 2. Protozoa | Amoeba |
| 3. Virus | Bacteriophage |
| 4. Algae | Chlorella |
| 5. Bacteria | Prokaryotic. |
![]()
4. State whether the following statements are True or False. Explain your statement:
Question a.
Lactobacilli are harmful bacteria.
Answer:
False.
Explanation Lactobacilli are useful bacteria. They are used for curdling the milk. They are also used for preparing variety of milk products.
Question b.
Cell wall of fungi is made up of chitin.
Answer:
True.
Explanation The cell wall of the plants is made up of cellulose while the cell wall of fungi is made up of complex sugar called chitin. Inside the fungal cell wall there is cytoplasm which contains many nuclei.
![]()
Question d.
Organ of locomotion in amoeba is pseudopodia.
Answer:
True.
Explanation Amoeba is a protozoan, primitive organism which possesses pseudopodia as the organ for locomotion.
Question e.
Tomato wilt is a viral disease.
Answer:
True.
Explanation: Tomato wilt is a viral disease. These viruses are able to infect only plant cells.
5. Give answers
Question a.
State the merits of Whittaker’s method of classification.
Answer:
For the answer of Merits of Whittaker’s method refer to point I of answer given on this Digest’s page no. 11; under “Use your brain power!”
Question b.
Write the characteristics of viruses.
Answer:
1. Viruses are extremely minute of the size range of 10 nrn to 100 nm. They are on the borderline of living and non-living. They are 10 to 100 times smaller than bacteria and are visible only through the electron microscope.
2. Though they are not considered as living, they can make replica of their own.
3. They exist in the form of independent particles. They are long molecules of DNA or RNA which are covered by a protein coat.
4. Their survival is possible only inside the living plant or animal cells. When they infect the host cells, they produce their own proteins with the machinery of the host cell. These proteins form many replicas of the infecting virus.
5. This infection destroys the host cell and the virus replicas are released. These free replicas re-infect the other adjoining cells of the host.
6. Most of the viruses are pathogenic, they cause diseases in plants and animals.
![]()
Question c.
Explain the nutrition in fungi.
Answer:
Most of the fungi are saprophytic in their nutrition. They absorb the nourishment from dead and decaying matter. By taking the organic matter from dead bodies of plants and animals, fungi survive. In this process they degrade the organic matter completely.
Question d.
Which living organisms are included in the kingdom Monera?
Answer:
- All the living organisms belonging to Kingdom Monera are unicellular.
- The mode of nutrition in them is either autotrophic or heterotrophic.
- All of them are prokaryotic and thus they do not have well-formed nucleus. The nuclear membrane and the cell organelles are absent in them.
- Kingdom Monera consists of different types of bacteria and blue-green algae.
E.g. Bacteria Clostridium titani, Vibrio choleri, Treponema pallidum, Streptococcus pneumoniae, Legionella pneumoniae, Salmonella typhi, Staphylococcus aureus, Clostridium botulinum.
6. Who am I?
Question a.
I don’t have true nucleus, cell organelles or plasma membrane.
Answer:
Microbe from Monera
Question b.
I have nucleus and membrane bound cell organelles.
Answer:
Protozoan from Protista/I am any one of Eukaryote
![]()
Question c.
I live on decaying organic matter.
Answer:
Fungus
Question d.
I reproduce mainly by cell division. (*Binary fission)
Answer:
Bacteria and some Protozoa.
Question e.
I can produce my replica.
Answer:
Virus
Question f.
I am green, but don’t have organs.
Answer:
Algae
7. Draw neat and labelled diagrams.
Question a.
Different types of bacteria:
Answer:
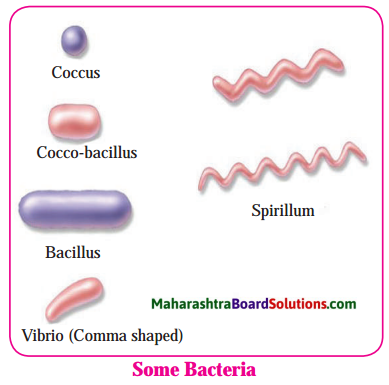
Question b.
Paramoecium:
Answer:
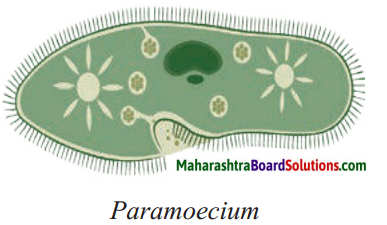
Question c.
Bacteriophage
Answer:
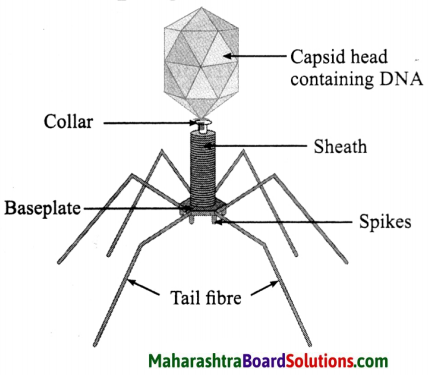
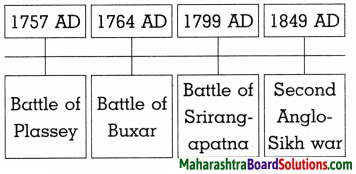
8. Arrange the following in ascending order of size Bacteria, Fungi, Viruses, Algae.
Question a.
Arrange the following ¡n ascending order of size Bacteria, Fungi, Viruses, Algae.
Answer:
Viruses, Bacteria, Fungi, Algae.
![]()
Project:
Question 1.
Prepare a chart showing infectious bacteria and the diseases caused by them.
Question 2.
Visit a nearby pathology lab. Get the information about pathogenic microbes, methods to observe them, different microscopes from the technicians there.
Class 8 Science Chapter 1 Living World and Classification of Microbes Additional Important Questions and Answers
Rewrite the sentences after filling the blanks:
Question 1.
The process of dividing living organism into groups and subgroups is called …………… .
Answer:
Biological classification.
Question 2.
Organisms with cell wall but not able to perform photosynthesis are called …………… .
Answer:
Fungi.
Question 3.
Most of the fungi are …………… .
Answer:
saprotrophic.
Question 4.
Viruses can be seen only with …………… .
Answer:
electron microscope.
Question 5.
…………… viruses attack bacteria.
Answer:
Bacteriophage
![]()
Question 6.
In fungi the cell wall is made up of j tough and complex sugar called …………… .
Answer:
‘Chitin’.
State whether the following statements are True or False. Explain your statement:
Question 1.
Plasmodium causes dysentery.
Answer:
False.
Explanation Plasmodium causes malaria. Entamoeba histolytica causes amoebic dysentery or amoebiasis.
Find out my partner
Question 1.
| Scientist | Pattern of classification |
| 1. Carl Linnaeus | (a) 5 groups of living organisms |
| 2. Haeckel | (b) 2 groups as Prokaryotes and Eukaryotes |
| 3. Chatton | (c) 4 groups as Monera, Protista, Plants and Animals |
| 4. Kopland | (d) 3 kingdoms – Protista, Plants and Animals. |
| 5. Whittaker | (e) 2 kingdoms of living organisms |
Answer:
| Scientist | Pattern of classification |
| 1. Carl Linnaeus | (e) 2 kingdoms of living organisms |
| 2. Haeckel | (d) 3 kingdoms – Protista, Plants and Animals. |
| 3. Chatton | (b) 2 groups as Prokaryotes and Eukaryotes |
| 4. Kopland | (c) 4 groups as Monera, Protista, Plants and Animals |
| 5. Whittaker | (a) 5 groups of living organisms |
![]()
Question 2.
| Living organism | Group |
| 1. Clostridium titani | (a) Heterotrophic Protista |
| 2. Paramoecium | (b) Fungi |
| 3. Chlamydomonas | (c) Bacteria belonging to Monera |
| 4. Baker’s yeast | (d) Algae |
| (e) Virus |
Answer:
| Living organism | Group |
| 1. Clostridium titani | (c) Bacteria belonging to Monera |
| 2. Paramoecium | (a) Heterotrophic Protista |
| 3. Chlamydomonas | (d) Algae |
| 4. Baker’s yeast | ((b) Fungi |
| (e) Virus |
Question 3.
| Microbes | Size |
| 1. Virus | (a) 1 μm to 10 μm |
| 2. Algae | (b) 200 μm |
| 3. Protozoa | (c) 10 μm to 100μm |
| 4. Bacteria | (d) 10 nm to 100 nm |
Answer:
| Microbes | Size |
| 1. Virus | (d) 10 nm to 100 nm |
| 2. Algae | (c) 10 μm to 100 μm |
| 3. Protozoa | (b) 200 μm |
| 4. Bacteria | (a) 1 μm to 10 μm |
Name the following/ Give examples
Question 1.
Three organs of locomotion in Protista
Answer:
- Pseudopodia
- Cilia
- Flagella
![]()
Question 2.
Two autotrophic Protista
Answer:
- Euglena
- Volvox
Question 3.
Institute in India which is involved in research on viruses
Answer:
National Institute of Virology, Pune
Question 4.
Two methods of asexual reproduction in Fungi
Answer:
- Binary fission
- Budding
Question 5.
Two pathogenic protozoans and the diseases caused by them
Answer:
- Entamoeba histolytica causes amoebiasis
- Plasmodium vivax – causes malaria.
Answer the following questions in one sentence:
Question 1.
What are the types of living organisms according to their lifestyle?
Answer:
Producers, consumers and decomposers are the types of living organisms according to their lifestyle.
Question 2.
What are the characteristics of prokaryotic cells?
Answer:
Absence of nuclear membrane, well- formed nucleus and lack of cell organelles are the characteristics of the prokaryotic cells.
![]()
Question 3.
When do virus destroy the host cells?
Answer:
After synthesising their own proteins and creating numerous replica of their own type, then the virus destroys the host cells.
Give answers:
Question 1.
Which criteria were considered for classification method of Whittaker?
Answer:
The criteria considered for classification by Whittaker are as follows:
1. Complexity of cell structure: Whether the cells of the organisms are prokaryotic or eukaryotic.
2. Complexity of organisms Whether the organisms are unicellular or multicellular is considered.
3. Mode of nutrition Whether the organism is autotrophic and is performing photosynthesis on its own or it is heterotrophic is considered. Plants are autotrophic, fungi are saprotrophic while animals use food from plants or other animals and hence they are heterotrophic.
4. Lifestyle According to nutrition, every living organism is at certain trophic level. This is called lifestyle. Plants are producers, animals are consumers while fungi are decomposers.
5. Phylogenetic relationship When the evolution proceeded gradually, there was transition from prokaryotes to eukaryotes, unicellular to multicellular. In this order the different groups of living organisms were evolved. This is known as phylogenetic relationship.
Use your brain power!
(Textbook page 3)
Question 1.
Explain merits and demerits of Whittaker’s classification.
Answer:
I. Merits of Whittaker’s classification:
- The classification system that Whittaker has adapted is totally based on scientific foundation.
- Prokaryotes are placed separately in a different kingdom. The prokaryotic organisms are different from other organisms, thus placing them separately is justified.
- All unicellular eukaryotic organisms are clubbed together in one kingdom named, Protista. This has helped to solve the placement of Euglena.
- Euglena has chloroplasts like plants but as animals it has flagella and thus there was conflict about such species during previous classification systems. It was placed in protozoa previously.
- Fungi are saprophytic and hence they are placed separately in a unique kingdom.
- According to five kingdom classification, the cell structure, organization of cell, mode of nutrition, lifestyle and phylogenetic relationship are taken into consideration.
- Therefore the system of 5 kingdom classification becomes most authentic system of biological classification.
II. Demerits of Whittaker’s method of classification:
1. Some organisms belonging to Monera and Protista have ability to perform photosynthesis. Thus they show mode of nutrition as autotrophic, while others are heterotrophic. Similarly some monerans have cell wall and some Protists also have cell wall. This becomes confusing during their placement.
2. In kingdom Protista, organisms show varied characteristics. In spite of this they are placed together.
3. In kingdoms, Plantae, Animalia and Fungi the organisms having primitive characters and were initial examples during evolution are not included. E.g. In Kingdom Animalia, amoeba is not included though it is said to be unicellular animal. This creates confusion.
4. Similarly if algae are unicellular, they are placed in kingdom Protista and if they are multicellular they are placed in kingdom Plantae. In reality, unicellular and multicellular algae both show much similarity. But due to Whittaker’s classification system they are placed away from each other.
5. Species of algae such as Chlorella, Chlamydomonas are not included in Kingdom Protista.
6. Viruses are not included in any of the kingdoms by Whittaker. Their classification has become a point of debate among the biologists.
Write short notes:
Question 1.
Characteristics of Fungi.
Answer:
- The organisms which are placed in kingdom Fungi are multicellular, heterotrophic, non-green, and eukaryotic in nature.
- Most of the fungi are saprophytic and they sustain on the dead and decaying organic matter.
- The cell wall of the fungal cells is made up of chitin. Chitin is the tough and complex sugar.
- Fungi have thread like body. The cytoplasm of the fungal cells contain many nuclei.
- The reproduction in Fungi is either sexual or asexual. Asexual reproduction is by fission or by budding.
- Examples Baker’s yeast, Candida, Mushroom, Aspergillus (Fungus on corn), Penicillium
![]()
Question 2.
Characteristics of Bacteria.
Answer:
- Bacteria are microscopic, unicellular, prokaryotic organisms belonging to the kingdom Monera.
- Some bacteria are solitary with independent existence. Some are colonial forms.
- The bacterial cell lacks well-formed nucleus with nuclear membrane and cell organelles.
- Reproduction is by binary fission.
- In favourable conditions, bacteria duplicate with a great speed. Within 20 minutes they can double in number.
- Bacteria may be round as in Cocci, elongated as in Bacillus, comma shaped as in Vibrio and spiral shaped as in Spirillum.
Question 3.
Characteristics of Protozoa.
Answer:
- Protozoa are unicellular, eukaryotic organisms belonging to kingdom, Protista.
- They are microscopic of the size of about 200 pm.
- They have different organs of locomotion such as pseudopodia, cilia and flagella.?
- Reproduction is by asexual method, usually by binary fission. .
- Protozoa are seen in varied habitats such as soil, fresh water and marine water.
- Some protozoans are parasitic and cause various types of illness in hosts. E.g. Entamoeba histolytica is a species of amoeba that causes amoebiasis. Malaria is caused by Plasmodium vivax.
- Protozoa show different modes of nutrition.
E.g. Euglena is autotrophic as it does photosynthesis with the help of 5 chloroplasts present in its body. Amoeba and Paramoecium are heterotrophic and free living seen in contaminated water.
Complete the paragraph using the words given in the brackets
[Monera, Euglena, autotrophic, cell organelles, chitin, nuclear, prokaryotic, viruses, replicas, saprotrophic, viral particles]
In Kingdom ……….. bacteria were included but not ………….. Viruses are on the border line of living and non-living. Do we really call them living? If they are making …………. of their own type, are they not considered as living? Throughout the world they spread hazardous epidemics. Antibiotics do not act on ………… However, bacteria can be controlled by antibiotics. All the living organisms belonging to Monera are with …………… cell. They do not have ………….. membrane and neither they have ……………… But a nice nucleus is seen in …………….., Euglena is ………… protist. The fungi with cell wall of …………….. are ………….. in their mode of nutrition.
Answer:
In Kingdom Monera bacteria were included but not viruses. Viruses are on the border line of living and non-living. Do we really call them living? If they are making replicas of their own type, are they not considered as living? Throughout the world they spread hazardous epidemics. Antibiotics do not act on viral particles. However, bacteria can be controlled by antibiotics. All the living organisms belonging to Monera are with prokaryotic cell. They do not have nuclear membrane and neither they have cell organelles. But a nice nucleus is seen in Euglena. Euglena is autotrophic protist. The fungi with cell wall of chitin are saprotrophic in their mode of nutrition.
![]()
Complete the chart:
Question 1.
Draw a chart showing different types of Microorganisms.
Answer:
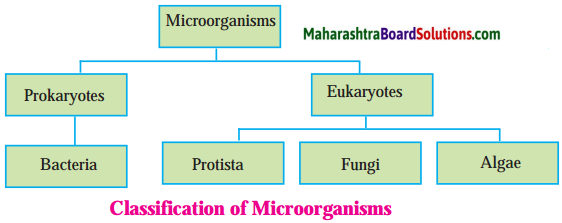
Draw neat and labelled diagrams:
Question 1.
Fungi:
Answer:
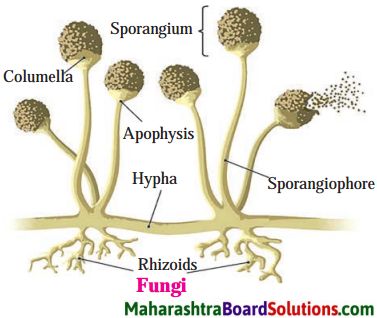
Question 2.
Euglena:
Answer:
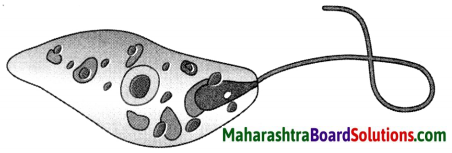
Question 3.
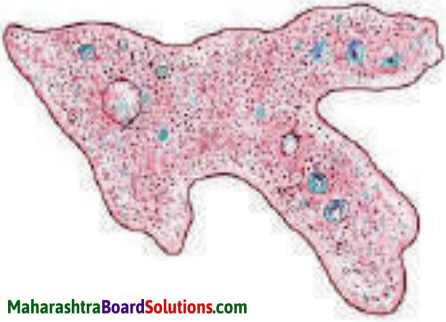
Amoeba:
Answer:
Question 4.
Correctly label the various organisms shown in the Kingdom Monera:
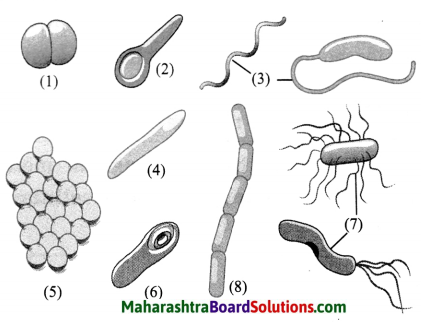
Answer:
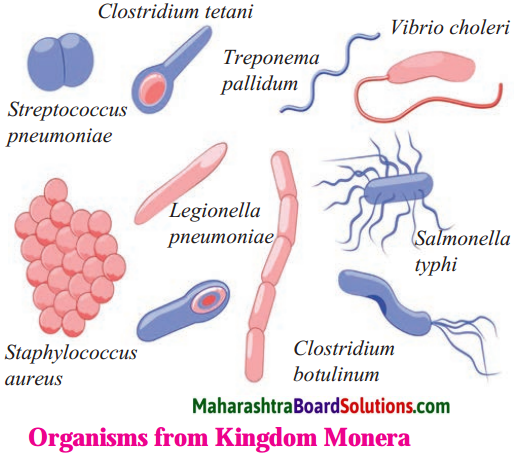
- Streptococcus pneumoniae
- Clostridium titani
- Vibrio choleri
- Treponema pallidum
- Staphylococcus aureus
- Legionella pneumoniae
- Salmonella typhi
- Clostridium botulinum
Activity-based questions
1. Try this:
Activity Take a small drop of curd or buttermilk on a clean glass slide. Dilute it with a little water. Carefully keep a coverslip. Observe it under high power of compound microscope. What did you see?
Answer:
In the slide we can see Lactobacilli \ bacteria.
2. Try this:
Activity Prepare a temporary mount of one drop of pond water on a glass slide. Observe it under low power and high power microscope.
Answer:
The drop on the slide shows motile microscopic organisms which have irregular shape. They are amoeba.
![]()
3. Try this:
Activity Take a moist piece of bread or bhakri and keep it in a container with lid for 2-3 days. After 2-3 days a fine cotton thread like tuft is found growing on the surface of the bread. Prepare a temporary mount of few threads from this culture and observe it under the microscope.
Answer:
Upon observation of thread like structures the fungal hyphae ( fibre like body) are seen.
MCQs based on experiments:
Choose the appropriate alternative of the following:
Experiment 1: To observe lactobacilli in curd/buttermilk.
Question 1.
Which of the following bacterium is used to make curds from milk?
(a) Streptococcus
(b) Lactobacillus
(c) Staphylococcus
(d) Clostridium
Answer:
(b) Lactobacillus
Question 2.
In which kingdom is Lactobacillus included?
(a) Monera
(b) Protista
(c) Fungi
(d) Plantae
Answer:
(a) Monera
![]()
Question 3.
Which is the other organism that has been added in kingdom Monera in addition to bacteria?
(a) Virus
(b) Blue-green algae
(c) Fungi
(d) Protozoa
Answer:
(b) Blue-green algae
Experiment 2: To observe fungus on the bread
Question 1.
In which kingdom is fungus growing on the bread included?
(a) Fungi
(b) Protozoa
(c) Monera
(d) Protista
Answer:
(a) Fungi
Question 2.
What are dark coloured particles which are seen when the fungus is growing on the bread?
(a) Sporangiophore
(b) Rhizoids
(c) spores
d) Columella
Answer:
(c) spores
![]()
Question 3.
Why is there growth of fungus on all the stale food?
(a) Fungus has affinity for food.
(b) Fungus grows on decaying organic matter.
(c) As food is open, the fungus drops on it and starts growing.
(d) None of the alternative is correct.
Answer:
(b) Fungus grows on decaying organic matter.
Class 8 Questions And Answers
8th Std Science Questions And Answers:
- Living World and Classification of Microbes Class 8 Questions And Answers
- Health and Diseases Class 8 Questions And Answers
- Force and Pressure Class 8 Questions And Answers
- Current Electricity and Magnetism Class 8 Questions And Answers
- Inside the Atom Class 8 Questions And Answers
- Composition of Matter Class 8 Questions And Answers
- Metals and Nonmetals Class 8 Questions And Answers
- Pollution Class 8 Questions And Answers
- Disaster Management Class 8 Questions And Answers
- Cell and Cell Organelles